63 of 100: 40 Matchsticks
The diagram above shows 40 matchsticks arranged in a square grid.
What is the fewest number of matchsticks that need to be removed so that there are no squares (of any size) remaining?
Try the problem on a smaller grid first.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Great answer. Does it follow though that there will be no 2x2 or 3x3 squares left, or is that down to your choice of matchsticks in the picture?
Log in to reply
Thanks Piers :) Both: for every interior removal of a matchstick, we eliminate 2 squares, so as long as one side of a square is removed, that whole square is eliminated. Since we considered all 1 5 remaining squares, it follows that squares of no size 1 × 1 are left. Can there still be 2 × 2 or 3 × 3 squares left? Yes and no, respectively. If four matchsticks removed are ill-placed in such a manner that they form a cross, then they will only form a 2 × 2 . Knowing that the minimum required is 9 , creating a 3 × 3 would require twelve ill-placed matchsticks to be removed. Great question!
Absolutely amazing, complete solution for problems of this kind: proof that nine is a minimum, and that nine is possible. And clearly explained in a (fairly :P) simple and (fairly :P) short way! Great job, Zach!
Log in to reply
The pleasure is mine. Thank you Angel! :)
Log in to reply
Hope you stick around to write solutions for all the other puzzles to come as well - I need this kind of clear explanation! :P
Log in to reply
@Angel Ong – Definitely will! I've contributed solutions to a few other 100 Day problems as well. Thank you so much! :)
Nice reasoning Zach :)
Nicely done, Zach! :)
Great solution!
Am also totally impressed - great solution
Smooth explanation:))
only eight stick is to be removed
This just eliminates the answer choice of ten. How do you know you can't do it with 8?
You still need the argument to eliminate 8. That is not difficult since one match can eliminate at most two 1x1 squares and with 16 1x1's that means at least 8 matches. But because the necessary match on the outside to eliminate the 4x4 can only eliminate ONE 1x1, eight matches that include removing the 4x4 can eliminate only 15 1x1's at most. A ninth match must be removed to eliminate the odd 1x1. Thus the minimum is at least 9.
Remove eight matchsticks to get rid of all inner squares.
Remove one more matchstick to get rid of the outer square.
What about the 2x2 squares, Nikita?
Log in to reply
not quite, there will be 2x2 squares left.
Log in to reply
Log in to reply
I made the same mistake, but luckily got the right answer.
Log in to reply
@Karl Snowsill – That means the problem is not good enough
It can't distinguish between really smart guy and not so smart lucky guy
To solve this properly two things must be done. 1. Prove that at least 9 matches must be removed. 2. Produce an example showing 9 achieved to eliminate 10.
-
Since one match can eliminate at most two 1x1 squares and with 16 1x1's that means at least 8 matches. But because the necessary match on the outside to eliminate the 4x4 can only eliminate ONE 1x1, eight matches that include removing the 4x4 can eliminate only 15 1x1's at most. A ninth match must be removed to eliminate the odd 1x1.
-
Shown in my FB album. I would post it here, but after I deleted an earlier incorrect solution I seem to be locked out from posting a correct one now.
(i ask the challenge master to enable me to post the correct solution graphic I have made to replace it and inside of 3 hours left.)
https://www.facebook.com/photo.php?fbid=1466867803358779&set=a.1133769940001902.1073741832.100001067207093&type=3&theater
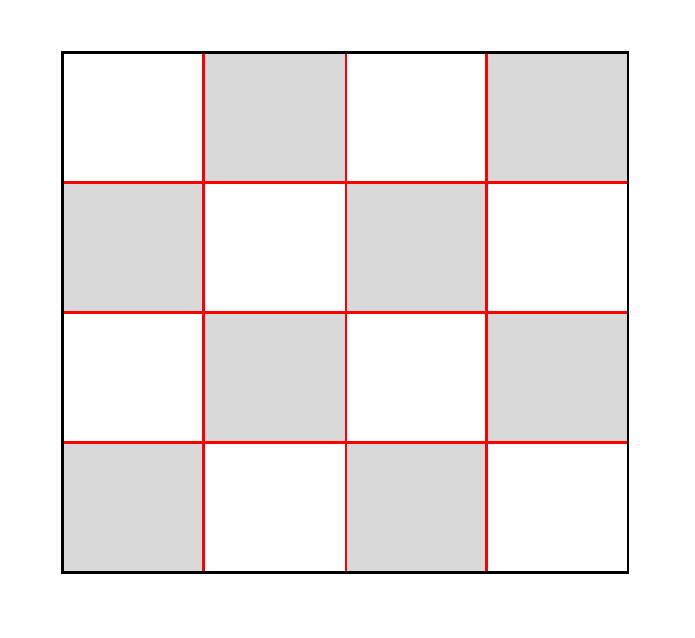 Consider all the shaded squares . They don't have any mutual sides so we have to remove 1 matchstick per shaded square
→
8 matchsticks should be removed to eliminate these 8 squares .
Consider all the shaded squares . They don't have any mutual sides so we have to remove 1 matchstick per shaded square
→
8 matchsticks should be removed to eliminate these 8 squares .
We also need to eliminate the other squares . The best way is that each removed matchstick is also a side of a white square
→
a removed matchstick must be a mutual side of a pair of (shaded , white) squares
→
put squares into pairs . That's why we see lots of pairs in all the solutions .
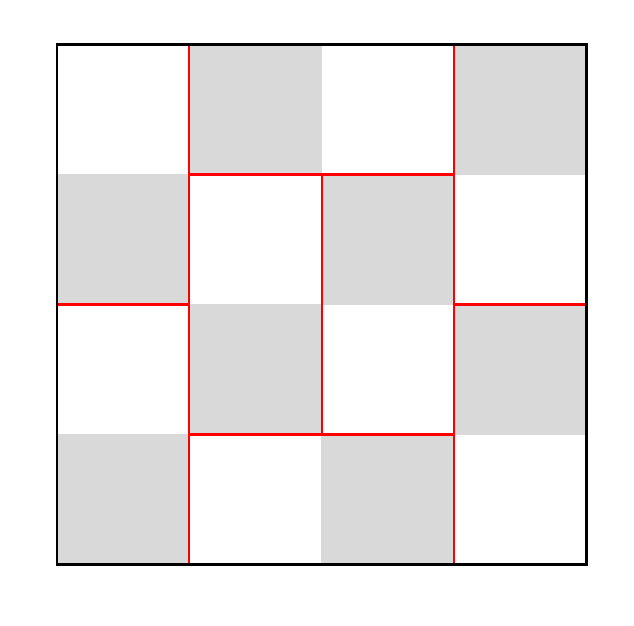 To eliminate the biggest square (black sides) , we have to remove 1 more matchstick . Hence , the answer is 8 + 1 =
9
.
To eliminate the biggest square (black sides) , we have to remove 1 more matchstick . Hence , the answer is 8 + 1 =
9
.
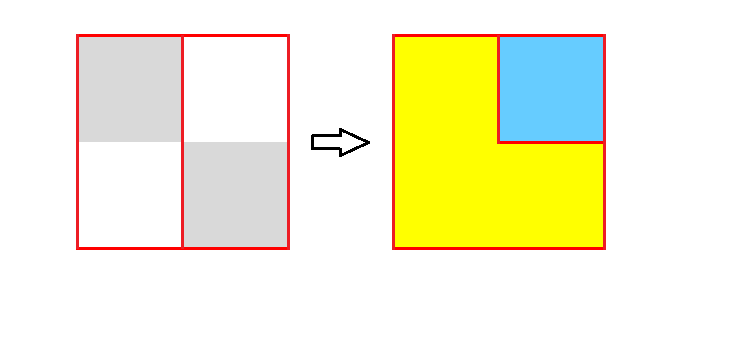
By the way , while arranging 8 pairs , it seems impossible to eliminate 2
×
2 squares . In this case , replace 2 pairs by a 1
×
1 square and the yellow thing (I don't know what to call it) or a 3
×
1 rectangle . This 1
×
1 square is eliminated together with the biggest square , which means at least one of its sides is black .
edit :
My old answer is wrong and this is my new answer :
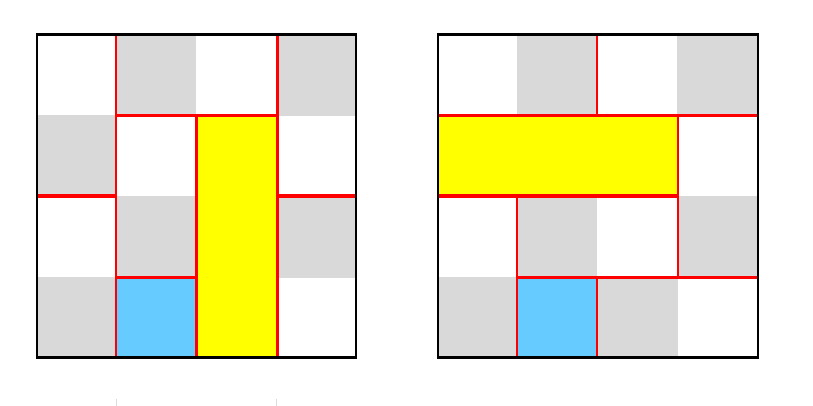
There is a 3 by 3 square in your answer.
That yellow figure is called a gnomon: https://en.wikipedia.org/wiki/Gnomon_(figure)
And it's true that there's a 3x3 square on the lower right. But you've also said you could have replaced it with a 3x1 rectangle. (Now I'm curious if it's impossible to produce a configuration that does not have the 3x1 rectangle, as all other answers here have that.)
Sorry for my big mistake and thank you for letting me know that . @Kevin Chris Marcelo , I've figured out that there are only 2 solutions (without reflection and rotation) and both have a 3x1 rectangle . Gnomon and 3x1 rectangle are the only 2 figures that have an area of 3 square units . I've tried to get an answer with a gnomon by moving 9 matchsticks but it turned out to impossible . It would take more moving steps to form a figure that has an area of 4 or more so I think a 3x1 rectangle is the best way here .
Split the construction into symmetrical parts and you get 4 squares which can be further divided into 4 small square with a side of one match. To remove the square shapes we have to remove 2 matchsticks from each large square as such:
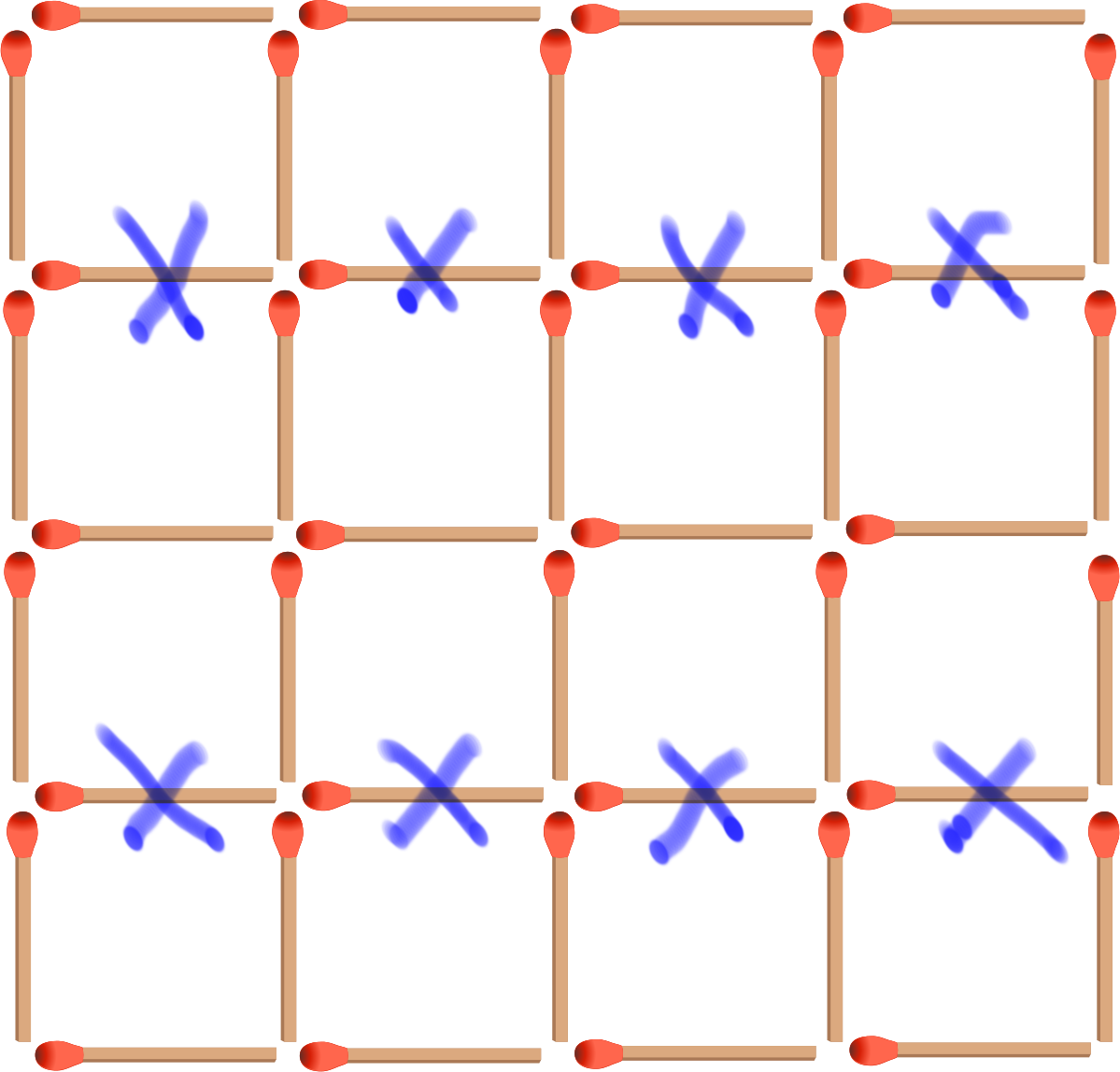
So that is 8 matchsticks so far. After that we also need to take into consideration the large square with a side of four matches which only requires the removal of 1 match.
8+1=9
There is an error in this solution - removing mataches the way you proposed leaves 2x2 squares intact.
ERROR ALERT
Remove the second and fourth rows of matches to create two rows of rectangles. Then take one more match out of the perimeter to get rid of the big square.
We can see this problem as a n-2 x n-2 grid with a level of boxes around it such that an n x n grid is formed (A grid inside another grid). Suppose now we know how to solve the problem in the inner grid, say C {n-2} sticks to be removed. Now for the outer line we have 4n-4 boxes. Just divide them by pairs until one is left. We have then 2n-3 sticks in our hands. For the last pair note we have the outer box so we cut one of the little ones and the big, leaving one little box of the outer line intact. We have removed then 2n-2. This same method can be applied to the interior grid making the last cut in the method such that takes account of the box we left before. Then we have C {n} =2n-2 + C {n-2} . The base cases are clearly C {1} =1 and C {2} =3. This formula leads to 9 for n=4. This has not the structure of a rigurous proof but it does well as a conjecture. I'll be glad if you guys can spot any mistakes or build further.
Before we remove any matches, there are sixteen (1x1) squares. For each one, we need to remove one of its four sides. If we remove one of the inside matches, then we can remove two of the sixteen squares. So we can get all of the (1x1) squares by removing eight matches. However, we also need to remove one of the outside matches to get rid of the (4x4) square. Therefore, we need at least nine matches.
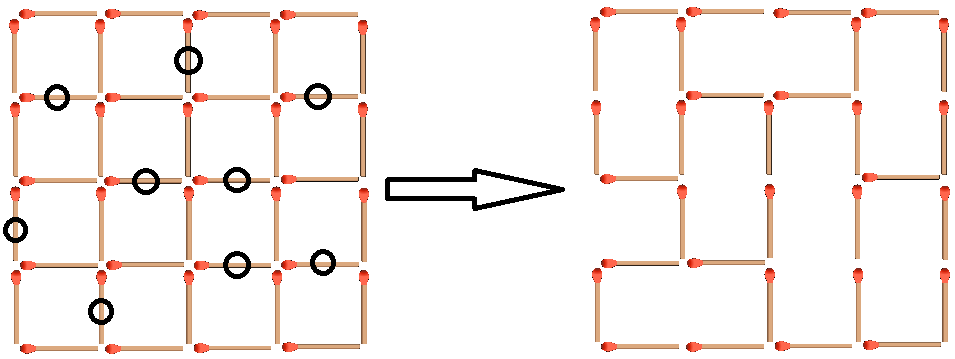
Consider first the outer 4 × 4 grid: one matchstick is required to be removed at a minimum, effectively eliminating one 1 × 1 square.
That leaves fifteen 1 × 1 squares. At most, how many squares can be eliminated by the removal of any given matchstick in the interior of the square grid? Two, since they share a common side. Thus, this will require ⌈ 2 1 5 ⌉ = eight matchsticks to be removed for a minimized total of 1 + 8 = 9 matchsticks removed.
All that is left is to show that this can be achieved: