68 of 100: Desert Trek
Sara needs to trek from an oasis to a destination 10 miles away across a barren desert.
The facts:
- Crossing one mile of desert requires using 1 gallon of water.
- Sara can only carry 6 gallons of water at a time.
- Sara can drop a water cache (of any amount of water from the supply she is carrying at that moment) at any of the nine stops along the route, and then pick up any part of the cache on a later trip.
What's the minimum number of times Sara must leave the oasis in order to cross the entire 10 mile span of desert?
Start by just trying to get Sara to her destination, then try to optimize!
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
15 solutions
Again, the problem is not set out explicitly enough - it should say (I think) she can never carry more than 6 gallons, otherwise, as Chethan says, she could go to the end in 2 trips. Aniswar - you can work out the possible options on a spreadsheet, but, fond as I am of spreadsheets, I think this is easier using pencil and paper.
If she is not always limited to carrying 6 gallons, couldn't you take two trips to milepost 1 for a total of 8 gallons there and then go all the way to milepost 10 on the third trip?
Log in to reply
Better, you could just drop off 4 at post 1 and go all the way on the second trip.
Log in to reply
@Chethan Bhateja Good point! And without 2 as an answer, my confusion on the 6-gallon limit is unfounded.
Yes, I didn't think of that. Thanks for pointing that out.
What is the computer science in this?
Good solution! Tried same approach, but couldn't make it this time :)
The question asks for how many times Sara leaves the oasis. [1. Leaves oasis with 6 gallons - 4 0 0 0 Back to Oasis] [2. Leaves oasis with 6 gallons - 3 3 0 0 Back to Oasis] [3. Leaves oasis with 6 gallons - 2 2 2 0 Back to Oasis] [4. Leaves oasis with 6 gallons - 1 1 1 1 Back to Oasis] [5. Leaves oasis with 6 gallons - 0 0 0 0 - Leave station with 6 and reaches 10.] So Sara leaves the oasis 5 times?
Log in to reply
The third step is unnecessary. I'll mark her current water and location with parentheses. So after step 2: 3 3 0 0 she heads off: 3(5) 3 0 0 - 2(6) 3 0 0 - 2 3(5) 0 0 - 2 2(6) 0 0 - 2 2 0(5) 0 - 2 2 2(3) 0 - 2 2 2 0(2) - 2 2 2 1(1) - 2 2 2(0) 1 - 2 2 1(1) 1 - 2 2(0) 1 1 - 2 1(1) 1 1 - 2(0) 1 1 1 - 1(1) 1 1 1 and with that we just skipped to your step 4. So she only needs to leave 4 times.
The correct solution is 4.
Trips 1, 2, and 3 are used to drop 4 gallons each at milepost 1 for a total of 12 gallons. Trip 4 can get 5 more gallons to milepost 1, for a total of 17, because Sara does not need to return to the oasis. So the total times she must leave the oasis is 4.
Sara continues by picking up 6 gallons, dropping 4 off at milepost 2, and returning. She picks up 6 more gallons, drops 4 off at milepost 2, and returns. Then she picks up the remaining 5 gallons and drops 4 off at milepost 2, with no need to return to milepost 1. Milepost 2 now has 12 gallons.
Sara now picks up 6 gallons from milepost 2, drops 2 gallons at milepost 4, and returns to milepost 2. She picks up the remaining 6 gallons from milepost 2, and drops 4 gallons at milepost 4, with no need to return to milepost 2. Milepost 4 now has 6 gallons.
Finally, Sara picks up 6 gallons from milepost 4, and arrives at milepost 10 with no water to spare.
How do you know it's impossible to reach the destination with 3 or less times leaving the oasis?
Log in to reply
I used a different method, but you can reason it out to be pretty sure either way. She needs to have a full six gallons at stop Four to make it all the way, and so four gallons must be deposited for the four she will spend getting there. It is impossible to deposit four gallons in one trip; they would be useless if they were all at stop One since she can only carry six at time. At least one of her gallons has to be left at stop Four because she uses a gallon getting from Three to Four and needs one there to refill for the rest of the trip. It takes three trips to place four gallons in the correct places and then she must return to refill for the final trip. Or you could use the method above but it still takes the same number of trips as you still need to have a full six at stop Four.
Log in to reply
That's good. My point is, for a proper solution, it must be proven that 4 trips is the smallest number possible. That's not fulfilled by only proving that it is possible to make it in 4 trips, it also has to be impossible to do in 3 trips or less. The reasons for this should be added to the solution.
Log in to reply
@Tarmo Taipale – Yes I realized that and tried to explain my semi proof. I proved to myself that four is the smallest number of trips with that approach, but perhaps there's a better approach. I wish I could definitively prove it, but I can't
I have fixed the issue.
I believe Clive above found a solution optimised for leaving the oasis that is more efficient than the content writer expected! I suspect the content writer solved for fewest miles covered, which I believe is a 5 oasis leaving solution.
I was interested to find that Clive Dawson's solution Andrew Lamoureux's both require 24 miles of walking for Sara.
"and then pick up any part of the cache on a later trip." You can't pick up the same cache on the same trip. So your solution violates the rules since she would be dropping and picking up the same caches on trip 4.
@Hope Odhner - only just seen this - excellent point - will come back to this later. The point with so many logic problems is not finding a solution, but proving that it is a unique solution
The other solutions give an example of Sara leaving the oasis 4 times so I'll just prove why 4 is the minimum.
The last time Sara leaves the oasis, she can bring 6 gallons of water and pick up 4 gallons of water on the stops to reach the end. The 4 gallons must be placed in a way that allows Sara to carry all of them and not run out of water before she reaches them. In other words, the first gallon she encounters must be between stops 1 and 6 inclusive, second gallon between stops 2 and 7, third gallon between stops 3 and 8, and fourth gallon between stops 4 and 9.
Every other time Sara leaves the oasis, she can bring 6 gallons of water to redistribute the amount of water at the stops.
Each gallon of water at stop 1 costs at least 4 6 = 2 3 gallons of water from the oasis, because placing water at stop 1 from the oasis requires 2 gallons of water for traveling, so at most 4 gallons of water can be placed for every 2 gallons of water wasted.
Each gallon of water at stop 2 either costs at least 2 3 gallons of water from stop 1 (following the same logic as above) or 2 6 = 3 gallons of water from the oasis (at most 2 gallons placed for every 4 gallons wasted). 2 3 gallons of water from stop 1 is equivalent to ( 2 3 ) 2 < 3 gallons of water from the oasis, so each gallon of water at stop 2 costs at least ( 2 3 ) 2 gallons of water from the oasis.
Continuing this process, each gallon of water at stop k costs at least ( 2 3 ) k gallons of water from the oasis.
The first gallon of water Sara encounters costs at least 2 3 gallons of water from the oasis because it must be between stops 1 and 6 inclusive. Similarly, the second, third, and fourth gallons of water Sara encounters must cost at least ( 2 3 ) 2 , ( 2 3 ) 3 , and ( 2 3 ) 4 gallons of water from the oasis, respectively. 2 3 + ( 2 3 ) 2 + ( 2 3 ) 3 + ( 2 3 ) 4 = 1 2 . 1 8 7 5
To place the 4 gallons of water, at least 1 2 . 1 8 7 5 gallons of water from the oasis were used, so Sara needed to leave and come back to the oasis at least ⌈ 6 1 2 . 1 8 7 5 ⌉ = 3 times. Including the last time Sara leaves the oasis, she must leave at least 4 times in total.
deserves to be no.1 solution for this problem
With your calculations I was able to prove that the most water surplus she can have when she sets off from oasis 4 with the 6 gallons needed to finish the trip would be 3, which also means that she can arrive at stop #10 with at most 1 extra gallon of water. There is only one solution to make this happen, but there are many solutions for her to make it all the way by leaving the oasis only 4 times, without having any water left to spare at the end. To calculate this you just have to take the upper floor of the amounts needed individually, which would result in 15 gallons needed instead of 12.1875, and take 15%6, which is 3. This is because she can only have integer amounts of water at any of the stops, either with her or dropped off.
Also, there is a slight problem with your solution because of this: while it works with up to 14 stops, starting with 15 or more it doesn't work anymore. At 15, for example, it gives 9 (112.something gallons needed) instead of the actual 10 (118 gallons needed) necessary leavings of the oases. So while it works here, it's a bit coincidental. Elegant solution, nonetheless, and only by seeing it could I also figure out the even more correct one, so cheers.
This is how I thought of it originally, but then I thought of a simpler idea (though perhaps less mathematically rigerous):
To make the trip, Sara needs 6 gallons of water at mile 4. Because she can carry at most 6 gallons, there needs to be a cache at mile 4. The minimum number of miles traveled to drop a cache at mile 4 and return is 8 if we ignore the 6 gallon constraint. The 6 gallon constraint means she will need to use intermediate caches and more miles traveled, but it has to be done by traveling more than 8 miles. Because of this, she must use more than 18 gallons total (travel for cache(8) + cache(?) + final trip(10)).
If she only leaves the oasis 3 times, she will have
3*6 = 18
gallons of water available, which is not enough. She must therefore leave
at least
4 times.
Log in to reply
I sort of kind of get your reasoning, but this doesn't prove (mathematically) that 4 times would be enough, only that less than 4 is not enough.
Log in to reply
right, but showing an example (as the other solutions do, which the author points out) is enough to show that 4 would be enough.
Go to stop #2, leave 2 gallons, and go back to base. Repeat until there are 8 gallons at stop 2. Then go back again and refill, and then go to step 2 and refill.
This makes 5 times of leaving the base, and leaves us carrying 6 gallons, standing at step 2, which stores 6 gallons.
Now, go to step 4, leave 2 gallons, go back to step 2 and refill. Then go to step 4, refill, and go all the way to step 10.
So 5 times leaving the base is enough. Don't know how to prove it can't get lower though.
the answer is 4 though?
This is how I worked: Sara needs to have a minimum of 6 gallons when she reaches post 4, so she can cross the remainder of the desert easily. Working backwards, this is how the set up needs to be for the final trip:
Case 1: 1 gallon at each of the 4 posts
OR
Case 2: 4 gallons at post 4
Note: There may be other cases, but these are the 2 I came to the conclusion would require the least trips.
Case 1: 1. she drops 4 gallons at post 1 and returns. 2. picks a gallon up at post 1, drops 3 at 2 and returns (3 gallons at both posts, 1 and 2) 3. picks a gallon at each of the posts, 1 and 2, drops 2 gallons at post 3 and returns (now we are left with 2 gallons at each post) 4. picks a gallon from each post and drops 1 off at post 4 (now 1 gallons is left at each post) 5. since we now have 1 gallon at each post, Sara can pick a gallon at each post and will have 6 gallons when we reach post 4, which as stated above means she can reach her destination.
Case 2: To get 4 gallons at post 4, Sara would need to have 4 (or 2 if she fills it from post 2) remaining for her returning journey, so she can only deposit a maximum of 1 (or 2) gallon at a time (if she has 6 when she reaches post 4, she can automatically go home), so it would take at least 2 trips (not counted*) to fill post 4 (assuming we have 12 stacked up at post 2, which in turn requires at least 6 trips). That would make it a total of 7 trips (6 to stack up 12 at post 2, and then the last journey where she fills back to 6 gallons at point 4.
Keeping the 2 cases in mind, we can clearly see that she does not meed more than 5 trips
Edit:
Case 3:
After thinking about it, and also looking at other comments, I realized that this was not as effective as possible. So, I found a new way to do it in 4 steps:
trip 1: drop 4 gallons at post 1
trip 2: fill at post 1, drop 4 gallons at post 2, pick one gallon at post 1 and return home (so it now stands as 2-4-0-0-...)
trip 3: repeat trip 2 (0-8-0-0-...)
trip 4: fill at post 2, drop 2 gallons at post 4 and repeat 1 time. Now, she'll be at post 4 with 4 gallons. refill and leave for your destination.
Credits to Elizabeth Loudon for bringing this to my attention.
*the problem asks how many times she leaves the oasis and not how many backward trips she makes
If she leaves a gallon at post 3 & 4 in your third step of Case 1 she has 1 gallon at each of the first 4 posts (thus making step 4 unnecessary) and can therefore reach home on trip 4.
She must have 0 gallons of water at the end,2 gallons at 9 ,3 gallons at 8 and so on. Can we solve the problem using this fact
The strategy here is to drop 6 gallons at post 2. If n is the number of trips to post 2 (or times Sara has returned to the oasis), then:
6n - 4n = 6
2n = 6
n = 3
The number of times Sara has left the oasis is equivalent to one more than the number of times Sara has returned the oasis.
No, that does not work because she can carry at most 6 gallons. Coincidental, only.
When I solved it, it said she can carry at most 6 gallons FROM the oasis, which doesn't contradict my proof.
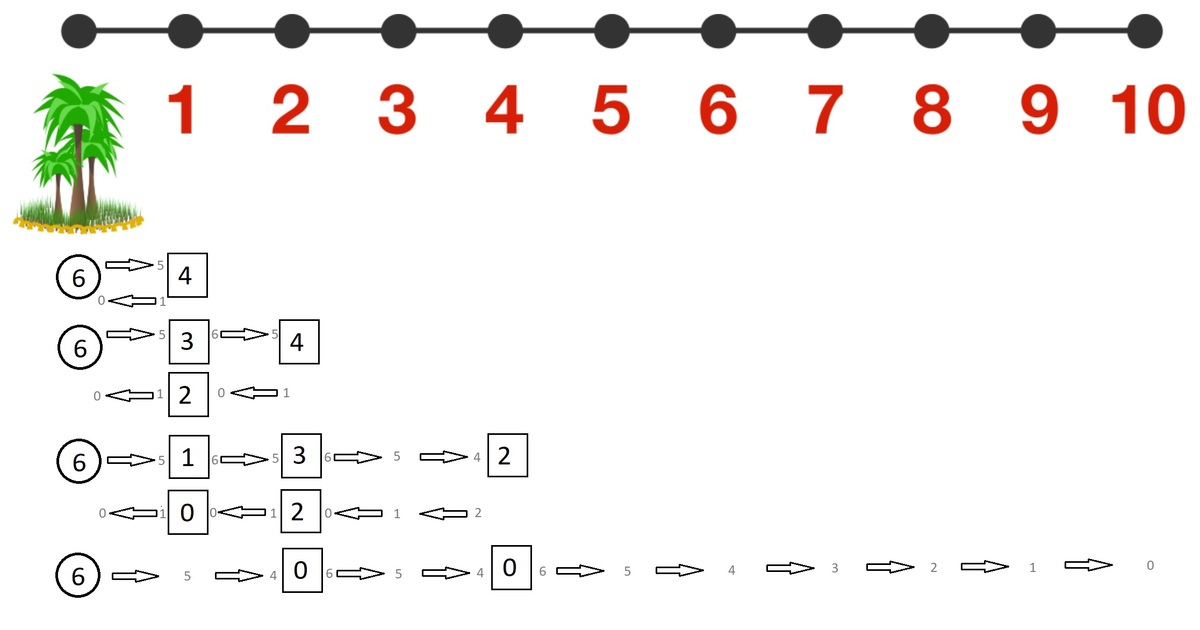
Sara needs to have 6 gallons of water when she is at post 4 in order to reach her destination. I mistakenly thought that each post could only hold up to 6 gallons of water, so here is my solution. Please note this is the first time I post a solution on Brilliant, and my skills on Paint are not great, but I hope this helps.
On the picture, a circle represents one trip, i.e. when Sara leaves the oasis. The number inside a square corresponds to the number of gallons left at the given post after an operation (drop or pick up water). A smaller number in grey (before or after an arrow) corresponds to the number of gallons Sara has left on her.
Take 6 gallons from the oasis and go to post 1: leave 4 gallons there and come back to oasis.
Take 6 gallons from the oasis; at post 1, refill with 1 gallon (only 3 gallons left at post 1), move to post 2 and leave 4 gallons there; come back to post 1 (with the only gallon left on you), take 1 gallon (2 gallons left at post 1), you are back at the oasis.
Take 6 gallons from the oasis and take 1 gallon at post 1 (1 gallon at post 1 now, and 6 on you). Move to post 2, take 1 gallon (3 gallons at post 2, 6 on you). Move to post 4, leave 2 gallons there, move back to post 2, take 1 gallon (2 gallons left at post 2) to reach post 1. Take the remaining gallon at post 1 and come back to the oasis.
Take 6 gallons from the oasis, move to post 2. Take the remaining 2 gallons of post 2. Go to post 4, take the remaining 2 gallons there: you have your 6 gallons to reach your destination. Be careful not to spill anything on the final way.
In the end, Sara left 4 times the oasis to cross the desert. I do not see how she could make with only 3, but this is not a proof that it is impossible (but at least it works with 4).
The solution is incredible tricky
It is impossible to explain it here
Refer to the JEEP PROBLEM
The correct answer is 4, not 5, and not that tricky.
Trip 1: Leave oasis with 6 gallons, drop 4 gallons at MP1, return to oasis. Trip 2: Leave oasis with 6 gallons, drop 4 gallons at MP1, return to oasis. MP1 now has 8 gallons. Trip 3: Leave oasis with 6 gallons, drop 4 gallons at MP1, return to oasis. MP1 now has 12 gallons. Trip 4: Leave oasis with 6 gallons, drop 5 gallons at MP1. MP1 now has 17 gallons.
She no longer has to return to the oasis, so the total times she had to leave the oasis was 4.
Continuing from MP1, pick up 6 gallons, drop 4 gallons at MP2 and return to MP1. MP1 has 11, MP2 has 4. Repeat this, and now MP1 has 5 gallons and MP2 has 8 gallons. Pick up the remaining 5 gallons from MP1 and drop 4 gallons at MP2. MP2 now has a total of 12 gallons.
Continuing from MP2, pick up 6 gallons, drop 2 gallons at MP4, and return to MP2. Pick up the remaining 6 gallons from MP2, and drop 4 gallons at MP4. MP4 now has a total of 6 gallons.
Finally, Sara picks up the 6 gallons from MP4, and arrives at MP10 with 0 gallons.
(How do I post this as a solution, rather than as a comment to a solution?)
Log in to reply
Write report to a problem
Well, if you want to post this as a solution, first you have to get the question correct, then you need to scroll to under the question where there is a space which says "Write your solution here", then well...you write it down then press preview, then Post!
Log in to reply
So I think what you're saying is that I first have to get the question wrong by clicking the wrong "correct" answer of 5, so that I can then post my solution with the right correct answer of 4. Or are you saying that you see a problem with my solution above, and the correct answer is not 4?
Log in to reply
@M F Hopper – What I'm trying to say is that Brilliant says the answer is 4, so you would have to click on 4 as your answer. Then, when you are typing your solution, you just have to write how to got to the answer (4). If you didn't click on 4 as your original answer, then you can't post a solution (even if you know how to get to the answer). If you think the answer is wrong, then you can report the problem (ask me about it is you want more information).
@M F Hopper – Mr Hopper, I recommend that you post a report to this question.
First you press the three dots at the bottom right of the question .
Then press view reports.
Then write a report (how you think it should be) in the "Write you report..." section.
I have already posted a report.
Thanks Nikita. I've never heard of the Jeep Problem but it's nice to know that there's an "ancestor" problem from which this one is derived.
Log in to reply
Initially that problem was "pure jeep problem" because the answer was 5
But some brilliant.org members quickly found unexpected solution with answer 4
So the author just wanted to make a jeep problem but made blunder
I used rates to solve this task and prove that the solution is optimal ...
Think about how much water Sara has (both carried and available at a stop). If that amount is 6 gallons or less then her optimal rate forward is 1 gallon per mile (i.e. 1 GPM). Sara wants to have 6 gallons of water available at the 4-mile stop to then optimally move forward across the rest of the desert. Her effective rate forward will depend upon the total amount of water that she is trying to move, under the terms of this task. Note that her actual rate, at any moment, is always 1 GPM and that she is restricted to carrying at most 6 gallons of water, at any moment. This enables a discussion in terms of her effective rate forward, as follows.
Between 6+ gallons and 12 gallons, her effective rate forward is 3 GPM since she will travel "forward toward the destination", "backward toward the oasis" and "forward toward the destination", each way consuming water at 1 GPM. Desiring to be at the 4-mile stop with 6 gallons of water, she should be at the 3-mile stop with 9 gallons of water or better yet, at the 2-mile stop with 12 gallons of water.
Between 12+ gallons and 18 gallons, her effective rate forward is 5 GPM (i.e. "forward", "backward", "forward", "backward" and "forward"). Desiring to be at the 2-mile stop with 12 gallons of water, she should be at the 1-mile stop with 17 gallons. At 5 GPM, she can't be at the oasis with 22 gallons of water since that violates the limit of 18 gallons of water for this rate.
Between 18+ gallons and 24 gallons, her effective rate forward is 7 GPM. Desiring to be at the 1-mile stop with 17 gallons of water, she should extract 24 gallons of water from the oasis. She can do this by extracting 6 gallons of water 4 times. Yay!
Obviously, she could extract more water and make it across the desert but her effective rate forward, initially, at between 24+ and 30 gallons of water is 9 GPM. This requires 5 extractions from the oasis and so isn't a better solution for the terms of this task.
Can she make it across the desert with less than 4 extractions? No! With 3 extractions she can carry at most 18 gallons of water. She will initially be using water at 5 GPM. After 1-mile she will have, at best 13 gallons of water which still requires a rate of 5 GPM to move all of that water forward under the terms of this task. Without adjustment, she arrives at the 2-mile stop with 8 gallons of water. She can now move at 3 GPM and arrive at the 3-mile stop with 5 gallons of water, which isn't enough to move her forward across the rest of the desert. At the 1-mile stop she could decide to adjust and abandon 1 gallon of water, to enable a lower rate (i.e. 3 GPM) but this only moves her forward as follows: 2-mile stop with 9 gallons and 3-mile stop with 6 gallons. Again, this is not enough to move her forward across the rest of the desert. At the 1-mile stop, she could also decide to abandon other amounts of water, in the hope of optimizing her effective rate forward, but none of these tactics enable her to make it across the desert. Three, or fewer, extractions of water (at the optimal 6 gallons per extraction) simply isn't enough water to fuel her trip across the desert.
Therefore, the best (i.e. least amount) she can do is leave the oasis 4 times, each time carrying 6 gallons of water. Moving all of that water 1 mile consumes water at an effective rate forward of 7 GPM, so she ultimately gets to the 1-mile stop with 17 gallons of water. She can now move forward at a lower rate, 5 GPM and arrives at the 2-mile stop with 12 gallons of water. She can then move forward at a lower rate, 3 GPM and will continue to do this for 2 miles, until she arrives at the 4-mile stop with 6 gallons of water. She then moves across the desert at her rate of 1 GPM, without needing to turn around.
A simplification is to observe that once she has 4 gallons at post 4 she can make it all the way . On the first trip she can get 4 gallons to post 1. She can get 4 out to post two on the second trip (with 2 at post 1), She can get 4 to post three on the third (with two at post 2 only), Then 4 to post 4 on the fourth. She "wastes" 2 gallons at post three but it's clear that's not enough to provide a three trip alternative.
There are 10 miles to cross and each mile takes one gallon of water. The water needs to last there and back so Sara can travel a maximum of 3 miles in one go. 10/3=3.333... This needs to be rounded up as Sara needs extra water not too little so the answer is 4.
To make the problem easier, we note that we only need to consider dropping water at bases 1-4, since otherwise we can drop all the water we dropped at a higher base at base 4 and still get through the desert.
Further, I will only consider tours on which the direction changes at most once (i.e. no multiple forward/backward movement between bases). This is not quite satisfying, but it makes the argument easier.
If we assume this, we can see that before the last trip straight through the desert, we must have dropped at least one gallon of water at base 4 (to have 6 when we leave it), and at least 4 gallons of water in total (since we need 10 to cross the desert but only start with 6). Hence, before our final trip, we must have reached base 4, gotten back and left 4 gallons on the way.
This makes at least 12 gallons of water used or left within the last preparational step. However, since water of at least one base needs to be used to reach base 4 and must've been placed at this base before, there needs to be some amount of water used for setting up this base.
Hence, strictly more than 12 gallons of water need to be used in the preparational steps, which implies that there are at least 3 preparational steps (or 4 starts in total).
To show that there is indeed a solution with 4 starts, I will give an example:
-
cache 4 gallons at base 1 and return
-
take one gallon at base 1. Cache 4 gallons at base 2. Return to base 1 and take a gallon. Return to start.
-
take one gallon at base 1. Take one gallon at base 2. Cache 2 gallons at base 4. Return to base 2 and take 1 gallon. Return to base 1 and take one gallon. Return to start.
-
take 2 gallons at base 2. Take 2 gallons at base 4. Go through the desert.
I attach a fairly long, but hopefully quite complete and illuminating solution. This solution emphasizes the "tree pruning" algorithmic method that is designed to solve by exhaustive search in a relatively efficient manner. I think that this is the same - or a very similar method that was used in the solution by Robert DeLisle, but with a slightly different presentation..
Notation: We describe the state of the system as (x1, x2, x3, x4) to represent the number of gallons of water at each of miles 1, 2, 3, and 4.
TRIP 1: Sara should take 6 gallons of water from the base. If she goes to Mile 1 and returns to the base, she uses 2 gallons for the trip and so can leave 4 at Mile 1. If she goes to Mile 2 and returns to the base, she uses 4 gallons for the trip and so can leave 2 at Mile 2. There is no sense in going to Mile 3 because then the trip requires 6 gallons of water and she cannot leave any water along the way.
So there are two possible results of Trip 1: A = (4, 0, 0, 0) and B = (0, 2, 0, 0).
TRIP 2A after (4, 0, 0, 0): First consider possibilities starting with (4, 0, 0, 0). Sara should start out with 6 gallons of water. If she only goes to Mile 1, she can leave 4 more gallons there for a total of 8 for outcome (8, 0, 0, 0). If instead, she goes to Mile 2, she takes 6 of those 8 gallons from Mile 1 and the trip takes two more gallons of water for resulting outcome (2, 4, 0, 0).
TRIP 2B after (0, 2, 0, 0): Next consider possibilities starting with (0, 2, 0, 0). If Sara starts with 6 gallons of water, travels to Mile 1 and returns to home base, the result is (4, 2, 0, 0). If she travels to Mile 2 and returns to home base, the result is (0, 4, 0, 0). If she takes all 4 gallons from Mile 2 to Mile 3, that extra mile of travel requires two gallons of water, so the result is (0, 0, 2, 0). Once again, there is no point in going to Mile 4, as this uses up all of her water. . So her possibilities after (0, 2, 0, 0) are (4, 2, 0, 0), (0, 4, 0, 0) and (0, 0, 2, 0).
TREE PRUNING STEP 2 : There are six possible outcomes after Step 2 from above:
C = (8, 0, 0, 0), D = (2, 4, 0, 0), E = (2, 0, 2, 0),
F = (4, 2, 0, 0), G = (0, 4, 0, 0), H = (0, 0, 2, 0).
It is desirable to reduce the number of subsequent calculations required to eliminate some of these options. We can eliminate D and E by comparison to B. In formal language, “D dominates F because each has 6 gallons of water in the system but D has additional gallons at Mile 2 rather than at Mile 1. B dominates G because B has 2 additional gallons at Mile 1 and the same number of gallons at Mile 2.“ Similarly, E dominates H because both have two gallons of water at Mile 3 but C has 2 additional gallons at Mile 1.
In addition, we can conclude that D must be at least as good as C because the only difference between them is that D includes an additional trip carrying 6 gallons from Mile 1 to Mile 2. That is, comparing C and D the 4 additional gallons at Mile 2 in D must be at least as valuable at the additional 6 gallons at Mile 1 in C., so we can eliminate C as a possibility, leaving only D = (2, 4, 0, 0) and E = (2, 0, 2, 0).
So there are two possibilities after two trips: D = (2, 4, 0, 0), and E = (2, 0, 2, 0).
One interesting observation is that the brute force analysis presented here can reveal useful insights about the nature of the solution. The result of tree pruning shows that in every case it is better to leave 4 gallons at Mile 1 rather than 2 gallons at Mile 2 in Step 1. This suggests a principle, which is that when you compare plans of action, you should prefer the one that allows Sara to carry six gallons to each next point in the desert wherever possible. Going all the way to Mile 2 at Step 1 is inefficient because she is only carrying 4 gallons from Mile 1 to Mile 2 when a different plan of action would allow her to make this trip at a later step with 6 gallons of water.
For the remainder of the analysis, we simply iterate this procedure, though with a growing number of possibilities to track.
TRIP 3D: With D = (2, 4, 0, 0) after Step 2, the possible results of Step 3 are I = (6, 4, 0, 0), J = (0, 8, 0, 0), K = (0, 2, 4, 0) and L = (0, 2, 0, 2).
TRIP 3E: With E = (2, 0, 2, 0) after Step 2, the possible results of Step 3 are M = (6, 0, 2, 0), N = (0, 4, 2, 0) and O = (0, 0, 4, 0), and P = (0, 0, 0, 2).
TREE PRUNING STEP 3: Comparing I, J, K, L, M, N, O and P: L dominates P. K dominates N and O. K is also better than J because it includes an additional step, moving 6 gallons from Mile 2 to Mile 3 at a cost of 2 gallons of water. This leaves four possibilities: I = (6, 4, 0, 0), K = (0, 2, 4, 0), L = (0, 2, 0, 2) and M = (6, 0, 2, 0).
The analysis could continue along similar lines for as many steps as necessary, EXCEPT that we can now observe that it is possible to go all the way across the desert from L = (0, 2, 0, 2).
So the answer is that it takes four steps to cross the desert and working backwards from L, we can see that the solution is A = (4, 0, 0, 0) in Step 1, then to D = (2, 4, 0, 0) in Step 2, then to L = (0, 2, 0, 2) in Step 3 and finally all the way across the desert in Step 4.
Very clear analysis. Unfortunately you made a few mistakes. At TRIP 2B you wrote (0, 0, 2). I think this should be (0, 0, 2, 0). Later on you wrote that there are three possibilities, called D and E. Aren't they two possibilities? And I think that at TRIP 3E there must be a forth result: P = (0, 0, 0, 2).
Thanks for taking the time to go through this proof in such detail. I followed up on the corrections suggested below and am submitting a new version that should be (I hope) correct.
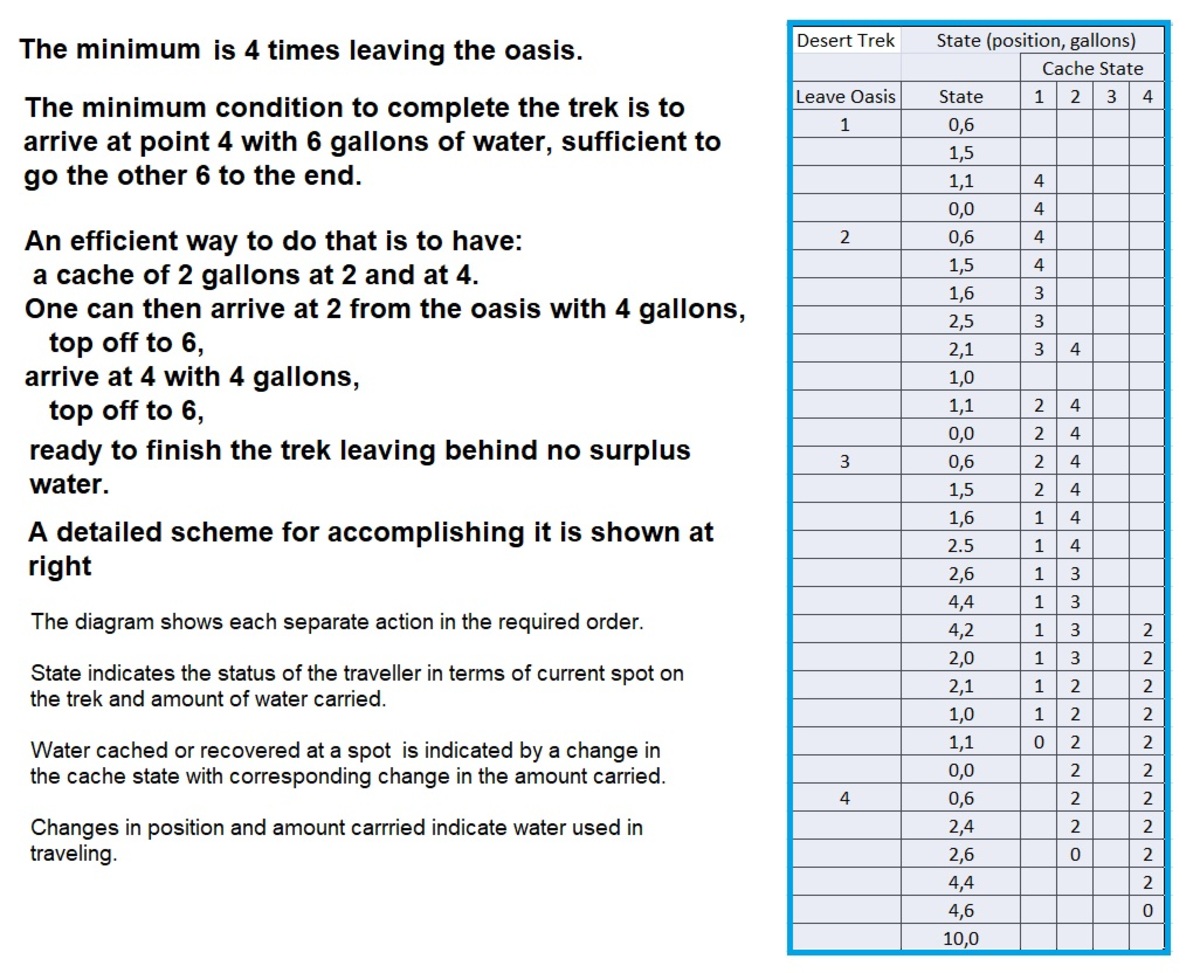

The solution is 4:
It's unclear if the 6-gallon limit only applies in the oasis case, or if she is always limited to carrying 6 gallons? Luckily the above steps satisfy even the second, more limiting rules.