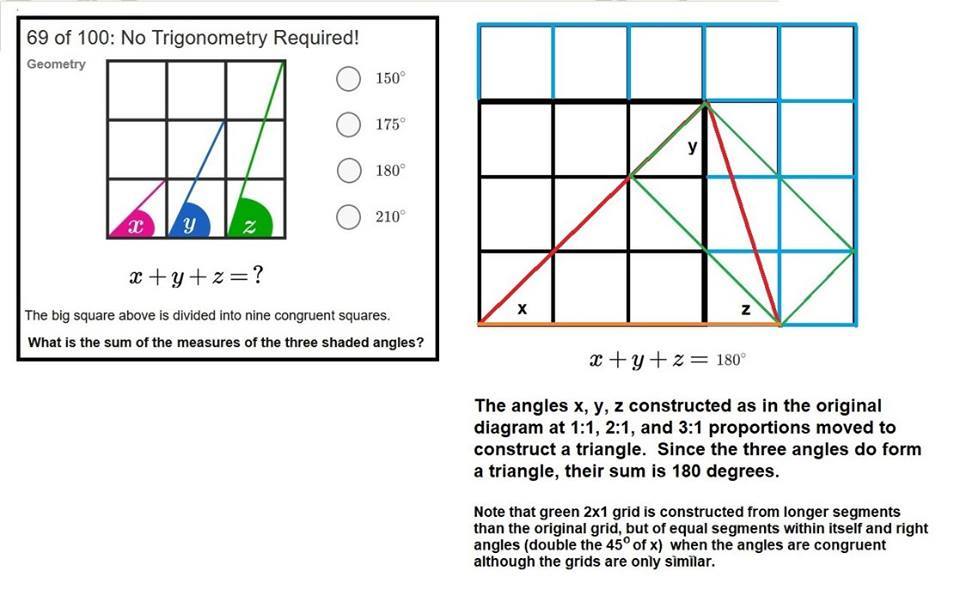
69 of 100: No Trigonometry Required!
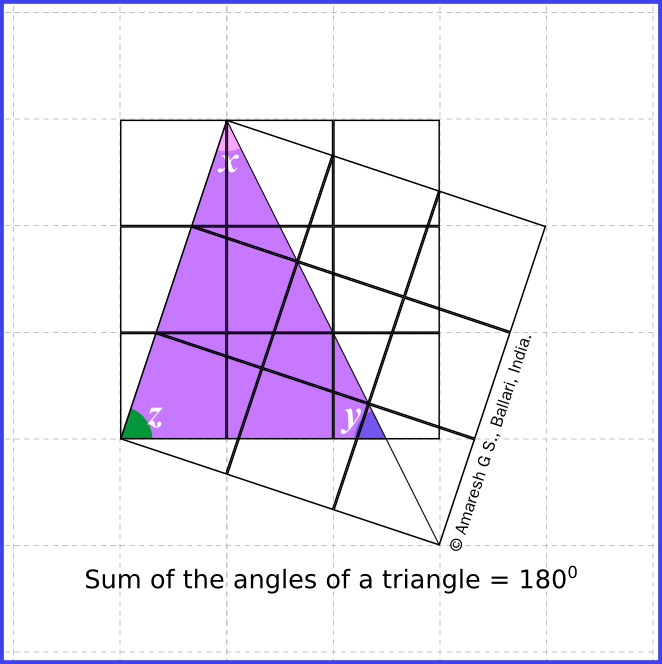
The big square above is divided into nine congruent squares. What is the sum of the measures of the three shaded angles?
As usual for the geometry problems in this challenge, there are many ways to approach this problem. For example, there's one clever technique that involves shifting the segments to different positions on the grid.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
26 solutions
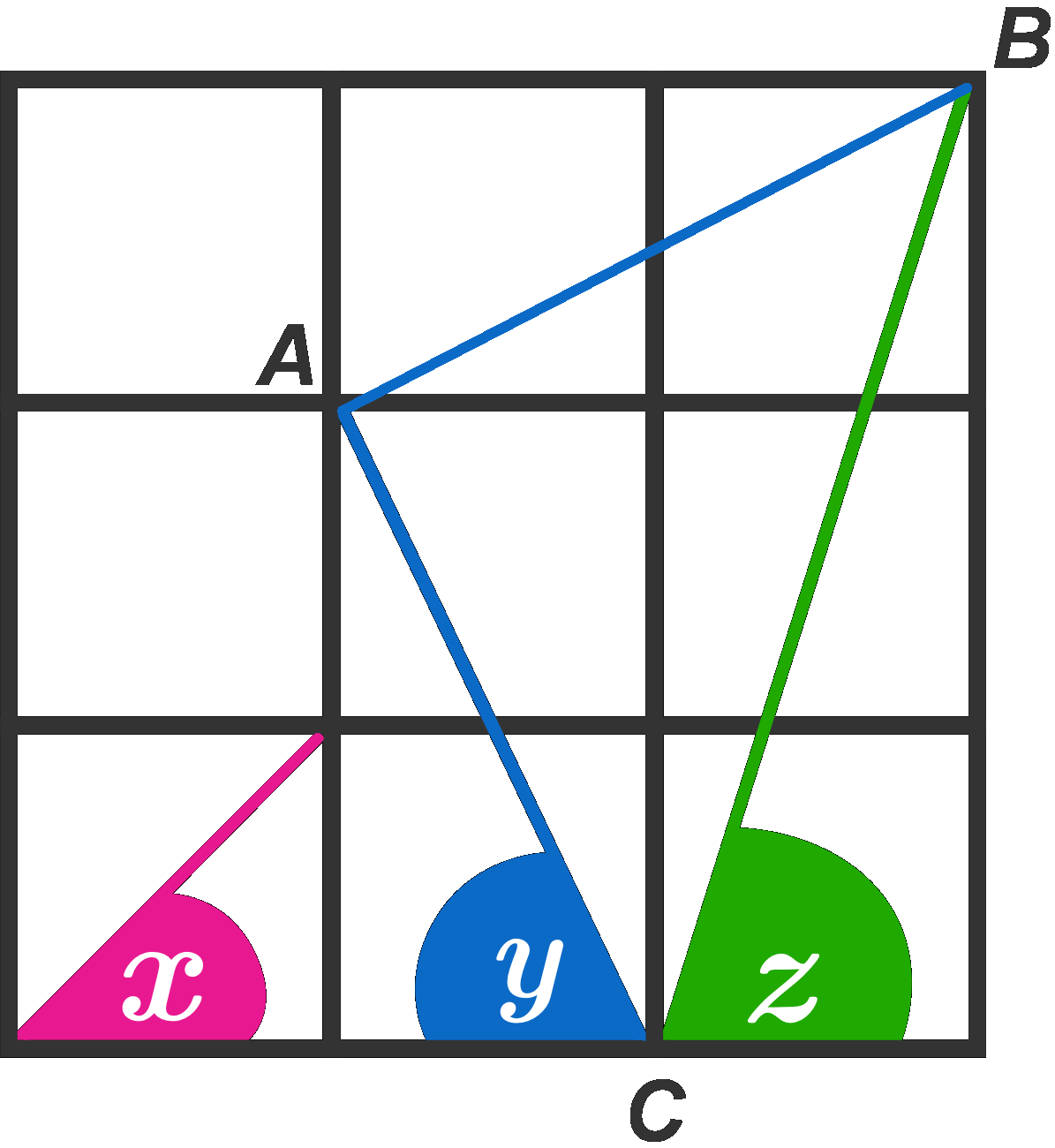 It's obvious that x = 45°. Mirror y vertically and try to figure out what the gap between y and z is. Looking at the grid you can see that AB = AC. Therefore in triangle ABC angle B = angle C. Also, noting that the slopes of AB and AC are negative reciprocals, you can see that angle A = 90°. Thus angle B = angle C = 45°. So x will perfectly fit into angle C. Conlusion: x + y + z = 180°.
It's obvious that x = 45°. Mirror y vertically and try to figure out what the gap between y and z is. Looking at the grid you can see that AB = AC. Therefore in triangle ABC angle B = angle C. Also, noting that the slopes of AB and AC are negative reciprocals, you can see that angle A = 90°. Thus angle B = angle C = 45°. So x will perfectly fit into angle C. Conlusion: x + y + z = 180°.
@Zach Abueg - If you replace "looking at the grid" with "noticing that the slopes of AB and AC are negative reciprocals", then I think that you have a fully satisfying solution.
Log in to reply
Yes! Perfect, thank you John.
I was waiting in the hope Michel would make the observation and change it, but since this answer is by far the most popular I went ahead and changed it for him. Michel, feel free to tweak the wording if you desire.
"Looking at the grid" is not enough to mathematically justify a result. Use the grid to supplement a proof, not to become one. For example, how do we know ∠ A = 9 0 ∘ ?
Log in to reply
@Michel van den Heuvel I think "looking at the grid" is fine for AB = AC -- the portions are absolutely congruent, just rotated -- but the 90 degrees does need an argument. It doesn't have to be a complicated argument, though.
Zach, you're back! :D anyway yes I was going to ask that, thanks! :P
Log in to reply
I won't be leaving this site any time soon, my friend :)
Log in to reply
@Zach Abueg – That's not what I meant... but that's cool too, I guess! :P Keep writing solutions and keep on solving puzzles, you're awesome! :)
Log in to reply
@Angel Ong – Oh no, I was just joking with you! Of course buddy :) And thank you!
Bacause tan a1 = 1/2 and tan a2 = 2/1, so tanA = (1/2 +2/1)/(1 - 1/2*2/1) = that wonderful theortical necessity ie infinity, so A (being less than 180, must be 90
https://m.youtube.com/watch?v=m5evLoL0xwg Far better solution
can anyone plz tell me that according to this solution how clealy is angle A=90
Nice. I had to use arctan for this one. Thanks for showing this idea.
This is what I did
Solution 1: Translation and Dilation
We can rearrange and resize the angles to get:
Solution 2: Addition through tangent identities
tan − 1 ( 2 ) + tan − 1 ( 3 ) tan ( x ) x tan − 1 ( 1 ) ⟹ tan − 1 ( 1 ) + tan − 1 ( 2 ) + tan − 1 ( 3 ) = x = tan ( tan − 1 ( 2 ) + tan − 1 ( 3 ) ) = 1 − tan ( tan − 1 ( 2 ) ) tan ( tan − 1 ( 3 ) ) tan ( tan − 1 ( 2 ) ) + tan ( tan − 1 ( 3 ) ) = 1 − 2 × 3 2 + 3 = − 1 = 1 3 5 ∘ = 4 5 ∘ = tan − 1 ( 1 ) + x = 1 8 0 ∘
https://m.youtube.com/watch?v=m5evLoL0xwg
Use complex numbers : ( 1 + i ) ( 1 + 2 i ) ( 1 + 3 i ) = ( − 1 + 3 i ) ( 1 + 3 i ) = − 1 − 9 = − 1 0 . In complex multiplication, the argument angles get added. The argument angle of − 1 0 is \fbox{\$180^{\circ}\$} .
Even if this solution is correct - actually being the same I've used to prove myself my first impression was correct - I think it can be considered a solution using trigonometry, but the title explicitly said that no trigonometry was required.
tan
−
1
3
+
tan
−
1
2
+
tan
−
1
1
=
π
=
1
8
0
∘
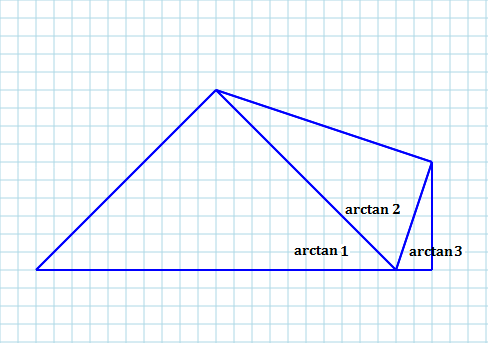
Proof: tan − 1 3 + tan − 1 2 + tan − 1 1 = tan − 1 1 − 3 × 2 3 + 2 + tan − 1 1 = tan − 1 ( − 1 ) + tan − 1 1 = tan − 1 1 + 1 − 1 + 1 = tan − 1 0 = π In the last step, we took the value of tan − 1 0 to be π as the summation of those three anges must be greater than zero.
Favourite solution, just not immediately obvious that the arctan 2 labelled is true:)
But the title was "No Trigonometry required" ?
Log in to reply
I didn't see the title at first. That's why I also added a trigonometric solution.
Log in to reply
I didn't notice it either, and forgot I had already written it up in my math puzzle picture album, saw the three tangents 1,2,3 right off, hit the calculator ATAN to get 180 in under a minute. Then I worked out the pure geometric solution again, but fortunately remembered that it was already in my FB album ready to repost here before starting another .jpg version.
Log in to reply
@Robert DeLisle – This happens to me also. I can rarely remember the problems I solve.
Log in to reply
@Atomsky Jahid – I still wasn't happy with the old one. Too busy. It has been replaced with a cleaner version in my solution post.
I don't think the trigonometry is relevant, the ratio of sides is the same as the original so only the total angle matters.
I got 45 for angle 1 67.5 for angle 2 and 75 degrees for angle 3
187.5 total
https://m.youtube.com/watch?v=m5evLoL0xwg
This is question # 6 9 , and it is clear that the number 6 is 9 rotated 1 8 0 ∘ . Mathematicians have a good sense of humour ⇒ the answer is 1 8 0 ∘ .
Quite elegant :)
I rearranged the shaded angles and voila! A bit wonky, but nevertheless, a straight line which (as we all know) is 180 degrees.
I knew x = 45 degrees because it would be exactly half of 90 degrees. Then, even though we didn't have to use trigonometry, I used a inverse trig functions (and a calculator) to find tan-1 (1/2) to find part of what was missing in triangle y. Tan-1 (1/2) is about 27 degrees, so < y would be 180 - 90 - 27 or 63 degrees. Then I used the same process to find < z. Tan-1 (1/3) is about 18 degrees, so < z = 180 - 90 - 18 or 72 degrees. Lastly I added 45 + 72 + 63 to get 180 degrees.
x is the argument of the complex number 1+i
y is the argument of 1+2i
And z is the argument of 1+3i
When complex numbers are multipled together there arguments add together
(1+i) (1+2i)(1+3i) = (-1+3i) (1+3i) = -10
The argument of -10 is 180° so x+y+z=180° QED
Draw the square whose vertices are ( 0 , 1 ) , ( 1 , 3 ) , ( 3 , 2 ) and ( 2 , 0 ) (grid coordinates). The angle formed by one of the sides and the diagonal is 4 5 ∘ = z − ( 9 0 ∘ − y ) , whence z + y = 1 3 5 ∘ and x + y + z = 1 8 0 ∘ .
atan(1)+atan(2)+atan(3)=180
The line segments are rearranged and extended to form three sides of a triangle. In the process the three shaded angles have become the angles of a triangle. And we know that the sum of all the angles of a triangle is
1
8
0
°
.
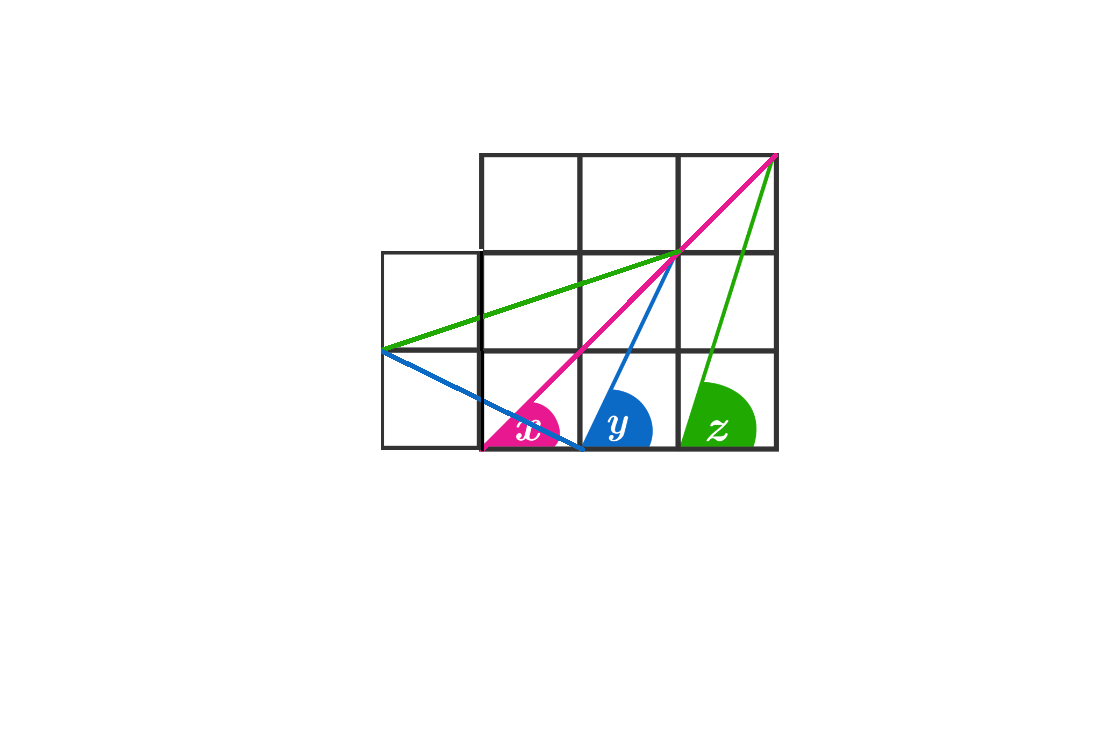
Adjacent leg of each angle is 1; opposite of x = 1; opposite of y = 2; opposite of z = 3.
Applying soh-cah-TOA, we need only find the arc-tangent of each quotient:
1 tan ^-1 = 45,
2 tan ^-1 = 63.43494882,
3 tan ^-1 = 71.56505118.
Adding the three arc-tangents together, we get 180 degrees.
x = 4 5 ∘
y = t a n − 1 ( 2 )
z = t a n − 1 ( 3 )
y + z = t a n − 1 ( 1 − 2 ∗ 3 2 + 3 )
= t a n − 1 ( − 5 5 )
= t a n − 1 ( − 1 )
= 1 3 5 ∘
x + y + z = 45 + 135
= 1 8 0 ∘
∠ x = 4 5 ∘
angle between pink line and blue line + angle between pink line and green line = 4 5 ∘
∠ x + ∠ y + ∠ z = 3 ∠ x + 4 5 ∘ = 1 8 0 ∘
Look at Michel Van den Heuvel's solution. Good solution. I'd like to prove this somewhat rigouriously using no visuals but the same basic idea. (Trigonometric proof)
Without the picture, we would just have to prove that 1) triangle ABC has the same ratio of cathethi as the x-triangle i.e. that tan ( ∠ C ) = 1 , and that
2) the triangle seen with those side lengths is actually right.
Name the given right triangles z-triangle, y-triangle and x-triangle respecticely.
1) This first result ist easily obtained, when you identify the construction of triangle ABC based on its hypotenuse and one cathesus. Inspired by the picture we carry on:
The pythagorean theorem provides that a right triangle with cathethis equaling the hypotenuse of the y triangle and hypotenuse equaling the cathehi of the y-triangle (that is ABC, right?) is of ratio 1.
These are 5 and ( 1 0 ) , And the resulting last cathethus is ( 1 0 − 5 ) = ( 5 )
2) To prove that ABC is right, I'll show that the right triangle constructed on the hypotenuse of the x-triangle and with hypotenuse along the z-triangles hypotenuse necessarily has to have its hypotenuse equaling the hypotenuse of the z-triangle. So for this right triangle we have
cos ( 1 8 0 − z − y ) = cos ( 9 0 − v ) for some v ∈ ( 0 ° , 9 0 ° ) (because the triangle is right, right?)
Carrying on with the cosine relation cos ( 9 0 − v ) = h y p o t e n u s e a d j a c e n t = h y p √ 5
Now since the hypothenuse of the triangle is along the z-triangle, we have
h y p = k ⋅ √ 1 0 for some real k.
Insert into the prior relation to get
cos ( 9 0 − v ) = k ⋅ √ 1 0 √ 5
⇕
cos ( 9 0 − v ) ⋅ k √ 1 0 = √ 5
⇕
cos ( 9 0 − v ) ⋅ k = √ 2 1
And thus we get that h y p = 2 1 1 0 = 2 1 0 = √ 5
And we are done. We've shown that given ABC is a right triangle with those side lengths, it has the same ratio as the right x-triangle and thus the same angles, and also that a right triangle with the given hypotenuse of √5 must be exactly ABC.
X is 45, and something from geometry 10 years ago stuck because I knew y is 60 and z is 75. No complex math just something about the 3x3 grid.
Except the angles are not 60 and 75. Plug 2, and 3 into the ATAN on your calculator to get the right values.
Each angle is initially given as a vector with respect to the Cartesian plane. First find the unit vector for x, (rt2/2, rt2/2). Then convert the plane to these units and use the new plane to rotate to the vector (1, 2) in terms of these units. Normalize this to a unit vector and repeat the process with the following plane.
The problem statement "No trigonometry required" and the solution choices make it a giveaway. 180 degrees is the only possible solution option that could be solved for without trigonometry.
The required angle sum can be expressed as x = a r c t a n ( 1 ) + a r c t a n ( 2 ) + a r c t a n ( 3 ) ⇒ a r c t a n ( 1 ) + a r c t a n ( 2 ) = x − a r c t a n ( 3 ) . . If we take the tangent of both sides, then we obtain:
t a n [ a r c t a n ( 1 ) + a r c t a n ( 2 ) ] = t a n [ x − a r c t a n ( 3 ) ] ;
or 1 − t a n ( a r c t a n ( 1 ) ) t a n ( a r c t a n ( 2 ) ) t a n ( a r c t a n ( 1 ) ) + t a n ( a r c t a n ( 2 ) ) = 1 + t a n ( x ) t a n ( a r c t a n ( 3 ) ) t a n ( x ) − t a n ( a r c t a n ( 3 ) ) ;
or 1 − 2 1 + 2 = 1 + 3 t a n ( x ) t a n ( x ) − 3 ;
or − 3 − 9 t a n ( x ) = t a n ( x ) − 3 ;
or 1 0 t a n ( x ) = 0 ⇒ t a n ( x ) = 0 ⇒ x = a r c t a n ( 0 ) .
Of the available choices, x = 1 8 0 degrees works.
x is the argument of the complex number (1+i), y that of (1+2i) and z that of (1+3i).
x+y+z is the argument of (1+i)(1+2i)(1+3i) = -10
Therefore x+y+z = 180 °
tan y = 2, tan z = 3, tan(y + z) = (tan y + tan z)/(1 – tan y tan z), tan(y + z) = -1, y + z = 135 degrees. Therefore x + t + z = 45 + 135
= 180 degrees.
I know this isn't a solution from myself, but I thought some might enjoy this relevant video.
Numberphile Video - The Three Squares Geometry Problem
For what's it's worth, my solution to the problem was the one that used the $tan(A+B)$ formula.
Tangent (y+z) is equal to -1 (by tangent sum identity)
So (y+z) is equal to 135 degrees