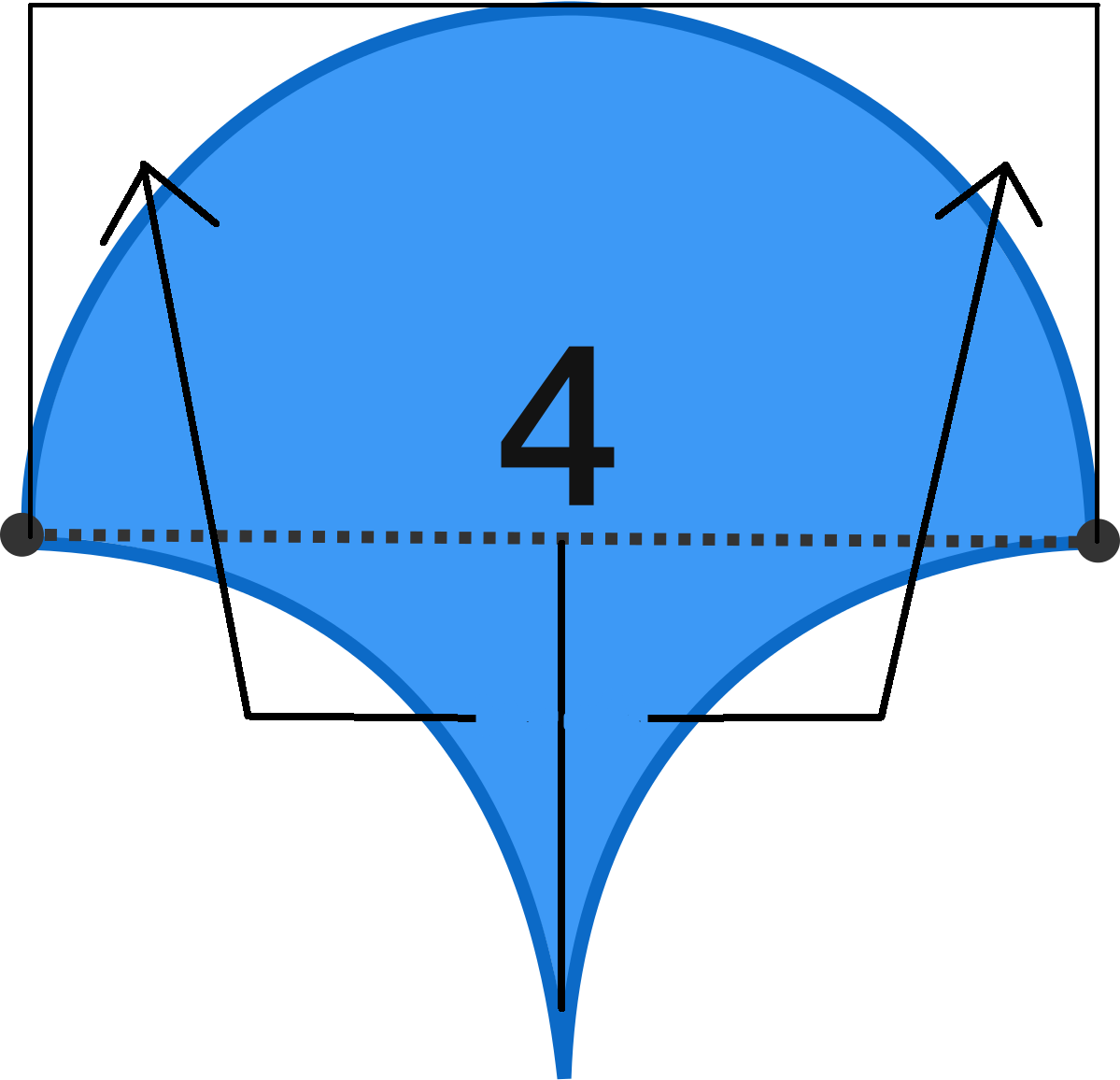
72 of 100: Fan

Geometry Level 1

What is the area of the blue figure?

Each arc is that of a circle of radius 2. The figure is symmetrical, the top portion is a semicircle with a diameter of 4 units, and the very bottom is a single point.

8 - \pi

8 - 2\pi

8

8 + 2\pi

12 solutions

Eric S
Aug 10, 2017

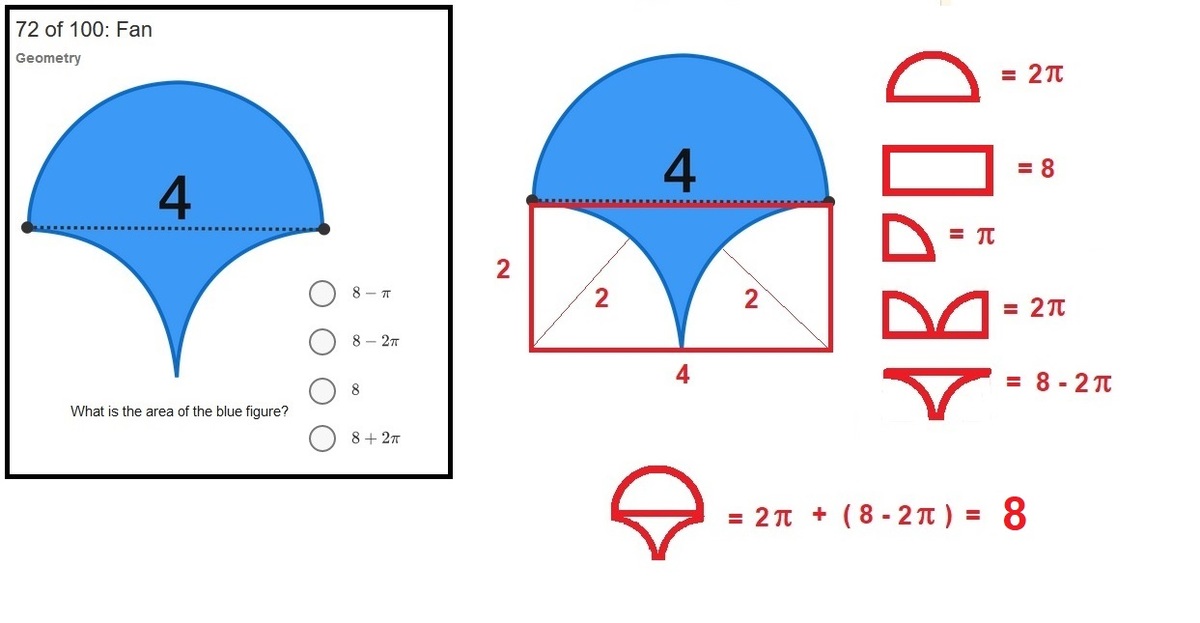
Divide the bottom in half, and put in in the top 2 corners. You should get a 2x4 rectangle which is equal to 8.

In a similar way, we can divide the top portion in half, and put each in the two bottom corners. We'll get the same figure anyway. :)

Efren Medallo - 3 years, 10 months ago

Now that is for sure! I'm not sure how I saw it one way but not the other.

Eric S - 3 years, 10 months ago

I know, right! I too saw it the other way around compared to yours. Hahaha

Efren Medallo - 3 years, 10 months ago

Wow...smart!

William Huang - 3 years, 10 months ago

the arrows should cross each other, otherwise the cut out pieces need to rotate

Mike Pannekoek - 3 years, 5 months ago

How do you draw these images? I mean which software/website you use?

Divyanshu Bansal - 3 years, 10 months ago

I use a windows operating system, I first right click the image and click 'save image as', and then I look for the image file, and right click it, then click open with, and I select paint. Later, when I upload my solution, I click the image picture at the top, and select the image file.

Eric S - 3 years, 10 months ago

thanks for telling.btw I found a website https://www.draw.io/ It looks pretty good to me (at least for now)

Divyanshu Bansal - 3 years, 10 months ago

Although it looks like the two lower arcs are tangent to the diameter of the senicircle and tangent to each other at their intersection, this is not a given and is only true when their radii are equal to 2 , which is not a given. A similar figure can be drawn for any radii for the lower arcs greater than 2. Therefore there is no unique solution.

Sridev Humphreys - 3 years, 10 months ago

You can't meet the conditions given (symmetry, bottom meets at a point, arcs are of circles) and have what you say be true.

Jason Dyer Staff - 3 years, 10 months ago

Not true. You can easily meet these conditions if the radii are greater than two.

Sridev Humphreys - 3 years, 10 months ago

It's implied that the arcs are tangent to the diameter of the semicircle but not noted. In fact, if the arcs on the bottom were of circles with longer diameters, the area would definitely increase. @Jason Dyer can you demonstrate why this is incorrect?

Joe Aulicino - 3 years, 10 months ago

Hm, I think the picture is pretty clear about it, but I went ahead and added something to the text just in case.

Jason Dyer Staff - 3 years, 10 months ago

@Jason Dyer – In a geometric problem, the picture really has no bearing on the solution. It is the written givens that matter. In this case we are given a semicircle and two arcs. The words were changed to state that all arcs have a radii of two. This was not stated in the original problem.

Sridev Humphreys - 3 years, 10 months ago

@Jason Dyer – Just in case, Hmm? Definitely needed that specification!

Guiseppi Butel - 3 years, 10 months ago

It is obvious that if you zoom in enough on the 'corner' connecting the semicircle and the arc, It looks extremely close to 90 degrees, therefore, the line I drew is 2, and if you shift the line over one of the 2 semi-semicircles, you see that the radii is 2.

Eric S - 3 years, 10 months ago

It has to be 90 degrees, because the tangent to a circle is always perpendicular to the radius from the tangent point.

Siva Budaraju - 3 years, 10 months ago

সাজিদ হাসান
Aug 10, 2017

I did this - but if I hadn't had the multiple choice answers, I'd have floundered. The joy of multiple choice is that each includes 8 - just a whole number, no pi, which points you to drawing a rectangle ('and the rest is obvious' - that's a joke you probably have to be a certain age to get)

Katherine barker - 3 years, 10 months ago

Yah, that 8 has made the rectangle obvious :p

সাজিদ হাসান - 3 years, 10 months ago

Robert DeLisle
Aug 11, 2017

The Eric S solution is better.

Are we assuming that the radii of the 2 bottom arcs is 2? Where does the problem specify this?

Guiseppi Butel - 3 years, 10 months ago

If the arcs intersect at the halfway up point of the circle (which they do), then when you look at the picture given by Brilliant, which has the intersection look like 90 degrees. The larger your circles get, the further the angle gets from 90 degrees. This is why the circle's radii have to all be 2 (diameter = 4). (Note, once you do this problem and look at the bottom of the 100 day page, it shows these fans all connected, and this is only possible if the arcs are of circles with diameter 4 or radii 2.)

Eric S - 3 years, 10 months ago

You can't possibly rely on looks. I can draw these arcs with any radius larger than 2.

Guiseppi Butel - 3 years, 10 months ago

It is a convention in these things that the 4 is meant to mean a full diameter of the upper semi-circle. That makes radius 2. That the lower quarter-circles start at the ends of that diameter and meet as quarter circles in the center puts them symmetrically at the center with radius 2. I consider that to be obvious pictorial representation of basic and obvious hypotheses in this situation. A lot is not stated, only drawn in these things. I hope you enjoyed your quibble.

Robert DeLisle - 3 years, 10 months ago

What specifies that the 2 lower arcs are semicircles? They are not!

Guiseppi Butel - 3 years, 10 months ago

@Guiseppi Butel – Semi-semi circles. Quarter circles. Fixed now. You are still making something out of nothing, as with the first comment. Give it up.

Did you miss this text in the problem itself? "Each arc is that of a circle of radius 2. The figure is symmetrical, the top portion is a semicircle with a diameter of 4 units, and the very bottom is a single point." Really, give it up.

Robert DeLisle - 3 years, 10 months ago

@Robert DeLisle – That "Each arc is that of a circle of radius 2" was added to the original problem. Why? Because the first wording lead to infinite answers! "Really, give it up" and admit that you are wrong! No amount of bluster and attacks makes it correct!

Guiseppi Butel - 3 years, 10 months ago

@Guiseppi Butel – I am not wrong. I took the problem for its obvious intention in the somewhat informal setting of this website, and I took it correctly. What is your problem? Why don't you study for your Ph.D. quals instead of arguing with me about what the website did or did not put on a simple puzzle aimed at a general public. Already have your doctorate? Why aren't you doing real research instead of hanging around here? Anyway you never had a real problem with me or my solution you had a problem with Brilliant.org. Take it up with them, and get off this comment thread.

Robert DeLisle - 3 years, 10 months ago

I too came up with the solution the same way Eric S did.

But I assumed like most people that the distance from The uppermost point to the point down at the bottom was also 4. And if it is, then 8 is right.

But the two cut out areas in the bottom wouldn't necessarily be out of the same size circle as the blue circle. And therefore the distance from the top point to the bottom point could be larger or smaller. If the problem had stated that the top-bottom distance was also 4, then fine. But it didn't. It looks about the same, but a drawing could be off too.

I saw that without the problem stating the top-bottom distance, the problem is unsolvable.
Agree or disagree?

Dave Gelineau - 3 years, 10 months ago

I agree. There could be an infinite set of solutions.

Guiseppi Butel - 3 years, 10 months ago

Hty Loid
Aug 11, 2017

The semi circle is 2x2x3.14/2=6.28 -> the answer must be bigger than that, so it isn't the first two. The circle, if complete, would be 2x2x3.14=12.56 -> the area has to be smaller than that, so it can't be the last one.

That leaves us with 8, the right answer!

Michael Schaap
Aug 11, 2017

8 is a correct answer, but not the only one. In fact, all numbers between 8 (inclusive) and 2π + 4 ≅ 10.28 (exclusive) can be a valid answer. Nothing in the problem description states that the bottom arcs are from a circle with the same size as the upper arc. Here's a possible variation where the bottom arcs have a diameter of 6.

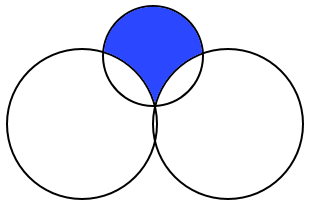
Any arc with a diameter of 4 or more works. As the arc diameter goes to infinite, the area goes to 2π + 4.

If the arcs intersect at the halfway up point of the circle (which they do), then when you look at the picture given by Brilliant, which has the intersection look like 90 degrees. The larger your circles get, the further the angle gets from 90 degrees. This is why the circle's radii have to all be 2 (diameter = 4). (Note, once you do this problem and look at the bottom of the 100 day page, it shows these fans all connected , and this is only possible if the arcs are of circles with diameter 4 or radii 2.)

Eric S - 3 years, 10 months ago

That's not how such problems work: an angle is only 90 degrees if it's stated to be 90 degrees, not if it only looks like 90 degrees in the diagram.

Michael Schaap - 3 years, 9 months ago

The problem clearly states that "Each (every) arc is that of a circle of radius 2."

Gordon Glenn - 3 years, 9 months ago

It does now. I'm fairly sure it didn't back when I posted this.

Michael Schaap - 3 years, 9 months ago

Miguel Angel
Aug 11, 2017

I think the problem needs to specify that the cusp at the bottom is such that the arcs meet tangent to each other; otherwise there could be multiple solutions of arcs just simply instersecting each other at a point in the middle of the figure to maintain symmetry.

Kevin Tong
Aug 11, 2017

The top of the figure is a semi circle of radius 2. The bottom is a 2 by 4 rectangle cut with 2 quarter circles of radius 2. The area of the 2 quarter circles cancel that of the semi circle, so what's left is $2 \cdot 4 = \boxed{8}$

Shreya Sinha
Mar 12, 2018

The lower part of the figure is the area left after cutting out a semicircle of radius 2 units from a rectangle of area (4X2)sq. units Thus area of lower portion of figure is 8-2 pi Again area of the upper portion of figure is 2 pi Therefore total area of figure is 8 sq units

Douglas Whitehouse
Aug 12, 2017

The area of the circle is 4 pi. The area of the half circle is 2 pi so the answer lies somewhere between 2pi and 4pi. 8 was the only solution that lies within this range. Had this problem not been multiple choice, I would defer to the other solutions.

Syrous Marivani
Aug 11, 2017

If we form a rectangle 4 by 2 at the lower half of the circle, the blue area = 8 - 2(1/4)(4pi) + 1/2(4pi) = 8.

Sina Asheghalishahi
Aug 11, 2017

Sundar R
Aug 10, 2017

The radius of the semi- circle is 2..The area is pi*2^2/2 = 2pi

The length of the sides of the rectangle are 4 and 2

The area of the blue shaded region in the bottom is area of rect - (area of 2 quarter circles of radius 2)

= area of rect – (area of top semi-circle)

= 8 – 2pi

The overall area of the blue region is : 2pi + 8 – 2pi = 8

72 of 100: Fan

12 solutions

0 pending reports