81 of 100: Ratio Riddle
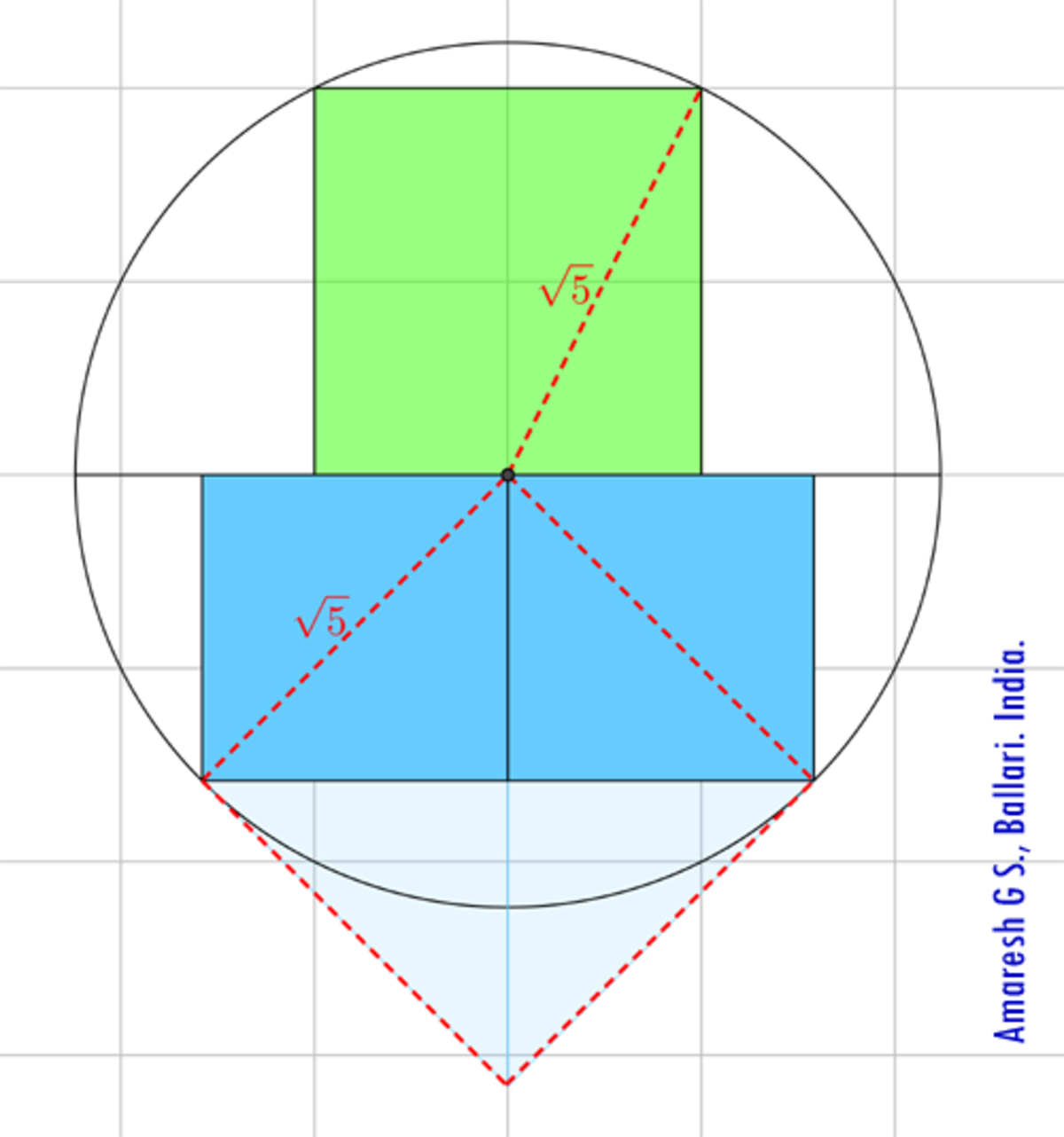
Two identical semicircles circumscribe one square and a rectangle composed of two squares, respectively.
What is the ratio of the green area to the blue area?
Hint: Look for ways to apply the Pythagorean theorem.
BONUS: Following the same pattern we've introduced for 1 and 2 squares, for what number of squares is the area of the squares the largest?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
Nice! You should tackle the bonus question. One can quickly show that if n is the number of squares inscribed in this way in the semicircle with radius 1, the total area of the squares is 4 + n 2 4 n . For instance, this gives the area of three squares as 1 3 1 2 . Optimizing using the derivative, you can prove that 2 squares indeed gives the maximum area.
Log in to reply
I have updated my answer to make room for the generalization. :) Please, ignore the bad quality of the images.
Log in to reply
Another fun result: the area for 4 squares is exactly equal to the area for 1 square: 5 4 r 2 . The reason for this becomes obvious when you use the mirror image idea: both cases correspond to inscribing in the circle a rectangle with side ratio 2:1.
Log in to reply
@Mark Lama – Well, it's sad that there's only one such pair!
Log in to reply
@Atomsky Jahid – Yes, since the area function is monotonically decreasing after the maximum at 2, there can only be one such pair. Cool, nonetheless!
Thanks - I teach primary and lower secondary children, who haven't reached calculus yet, but I am left musing that 1 is such a weak, weedy number that when you change n from 1 to 2, the area increases, but with all further increases in n, the denominator increases faster than the numerator, so the total area decreases. Come September, I may be teaching a couple of older kids - I hope it's ok if I copy your solution to a word document to keep.
Log in to reply
Showing the graph of 4 + n 2 4 n to the students who are studying pre-calculus might help. One can also find n=2 (for the max area) using inequalities! It's okay to copy. And, if you tell others about Brilliant.org then it will be better.
Suppose that
n
squares, with side
a
, are circumscribed in semicircle. We need to find
A
n
=
n
a
2
.
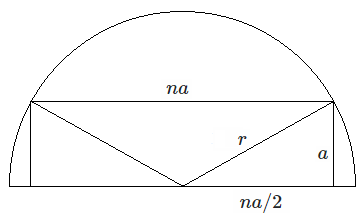 Apply the Pythagorean theorem
a
2
+
4
n
2
a
2
=
r
2
⟹
a
2
=
4
+
n
2
4
r
2
Thus
A
n
=
n
a
2
=
4
+
n
2
4
n
r
2
For this problem we have
A
1
/
A
2
=
(
4
/
5
)
/
(
8
/
8
)
=
4
:
5
.
Apply the Pythagorean theorem
a
2
+
4
n
2
a
2
=
r
2
⟹
a
2
=
4
+
n
2
4
r
2
Thus
A
n
=
n
a
2
=
4
+
n
2
4
n
r
2
For this problem we have
A
1
/
A
2
=
(
4
/
5
)
/
(
8
/
8
)
=
4
:
5
.
For bonus, write A n as A n = 4 + n 2 4 n r 2 = n 4 + n 4 r 2 = ( n − n 2 ) 2 + 4 4 r 2 ≤ r 2 Equality occurs when n − n 2 = 0 or n = 2 .
Let's do the general case for n squares in a row.
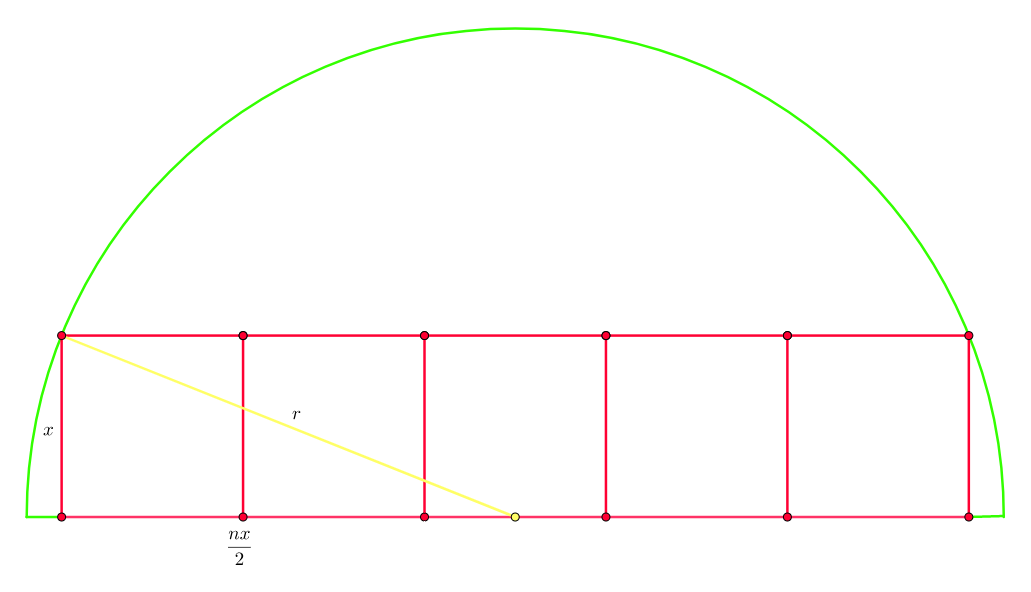
Let each square have side length x , and radius of the semicircle be r . Note that the total area of the rectangle will be n x 2 . Thus, by Pythagoras Theorem, we have r 2 n x 2 = ( 2 n x ) 2 + x 2 = x 2 ( 4 n 2 + 1 ) = n 2 + 4 4 n r 2
To maximise the area of the rectangle, we find the derivative of the RHS, optimise by equating to 0. d n d n 2 + 4 4 n r 2 0 1 6 r 2 − 4 n 2 r 2 4 − n 2 n = ( n 2 + 4 ) 2 4 r 2 ( n 2 + 4 ) − 2 n ( 4 n r 2 ) = ( n 2 + 4 ) 2 1 6 r 2 − 4 n 2 r 2 = 0 = 0 = 2
Note n = − 2 since n must be positive. Furthermore, n = 2 is the maximum since from the problem, we attained that the area of the 2 squares is greater than the area of the single square, so we get that n = 2 gives the maximum area.
Thus, 2 squares give the area of the squares to be the largest.
Let's pretend that the radius of each circle is x. We'll start from the semicircle with the green square. Connecting the upper corners of the square to the center of the circle, we create two radii of x length. Each radii is also the hypotenuse of a right triangle where the right angle is one of the bottom corners of the square. The shorter leg of each right triangle is half the side length of the square, and the longer leg is a side of the square. We'll give the shorter leg the value y, and the longer leg the value 2y. Using Pythagorean, 5y^2= x^2. That means y^2 = (x^2)/5. The area of the green square is (2y)^2 = 4y^2, which in terms of x is 4(x^2)/5. Now let's move to the two blue squares. Once again, the radius is x. Drawing in two radii from the outer upper corners of the squares to the center, we create two diagonals of x length each. As a diagonal of a square is sqrt(2) times its side length, the side of each square is x/(sqrt(2)). The area of each square is then (x^2)/2, giving the blue rectangle(the squares combined) a total area of x^2. The ratio of the green square to the two blue squares is 4:5 .
Unit semi-circle y = 1 − x 2
Side-length of the green square g = 1 − ( g / 2 ) 2
g 2 = 1 − 4 g 2
4 g 2 = 4 − g 2
5 g 2 = 4 Green area A g = g 2 = 5 4
Shortest side of blue rectangle: b = 1 − b 2
b 2 = 1 − b 2 Area of blue rectangle: A b = 2 b 2 = 1
Ratio of Green area to Blue area ∴ A g : A b = 4 : 5
A bit late, but I don't look here every day so I've only just seen this puzzle. I most certainly disagree with the "seriously spiky" rating.
The main question is very simple. The ratio doesn't depend on radius so I assumed radius=sqrt(5) because then one square has side 2 and area 4. The area of two squares is the square of a diagonal, which is radius, so 5.
Bonus is simpler than what others did. This time I'm assuming radius=1, so the area of 2 squares is 1.
Now let's imagine n squares along the diameter. The area of that is 4/n. But in order to fit n squares inside, they need to be slightly shrunk. Doesn't matter how much, the area is LESS than 4/n, so for n bring at least 4 it's less than 1 (two squares).
That just leaves us with 3 squares. Assuming radius sqrt(13), the side of a square is 2, so the area of 3 squares is 12, less than the area of 2 squares, which is 13.
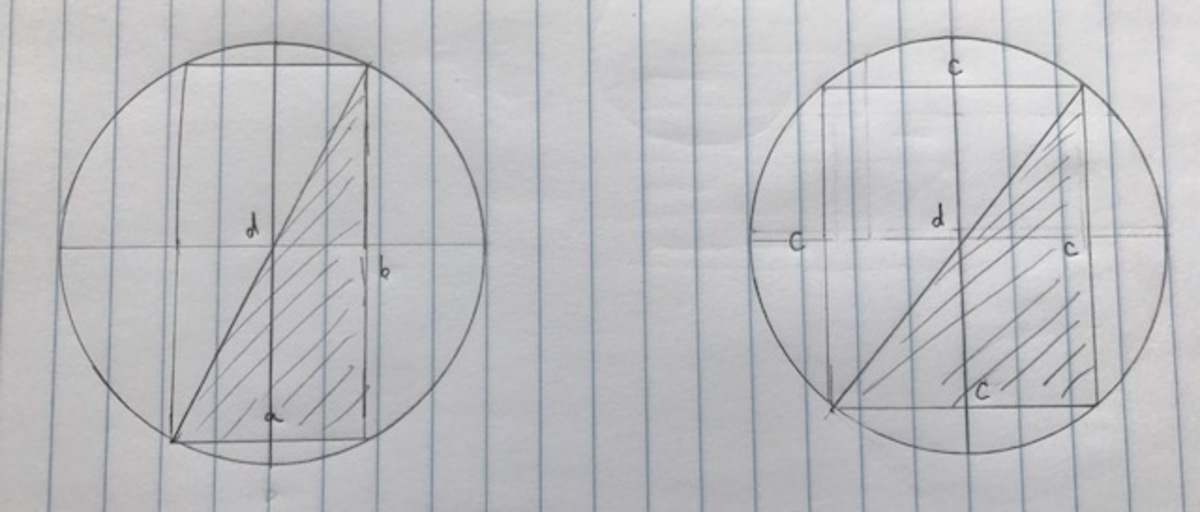
a = 2 1 b
Let a=1, b=2
Then d= 5
d is the diameter of both circles
Green area will be 2 1 ∗ 2 , so 1 sq. unit.
Blue is one quarter the area of a larger square with the side lengths of d, or 4 d 2
Blue then is 4 5 sq. units.
Multiply both by 4 giving the ratio 4:5.
Let r be the radius of both circles.
Blue squares---if r is the radius then the sides of each square must be r/square root of 2 each. Thus the area of the two blue squares is 2 r/square root of 2 r/square root of 2. Reduced the area of blue is rsquared.
Green--I used inverse tan to determine the angle from the center of the circle to be approximately 63.4 degrees. From that I came up with the equation sin63.4=s/r with s being the side of the green square. solving that equation for s yields s=.89r. Therefore the area of green = .89rsquared. This yields the area = .7995 rsquared. This rounds to the exact answer of .8rsquared.
So the green area must be just 4/5 of the blue.
Let the side of the green square be x and the sides of the blue rectangle be y and 2y. Also let
the radius of the circle be r, then we have:
r^2 = x^2 + (x/2)^2 and r^2 = y^2 + y^2.
Then,
x^2 = (4/5)r^2 and 2y^2 = r^2
Green Area/Blue Area = x^2/(2y^2) = 4/5.
this question is wrong please check as the answer is suppose to be 2:5
For the green square of side s, by the Pythagorean Theorem, we have s^2 + (s/2)^2 = r^2, or s^2 = (4/5)r^2. For the rectangle of sides m and 2m, the area = 2m^2. Again, by the same Theorem, we have m^2 + m^2 = r^2, or m^2 = (1/^2)/2, and 2m^2 = r^2. Therefore the area of green to blue = (4/5)/1. Ed Gray
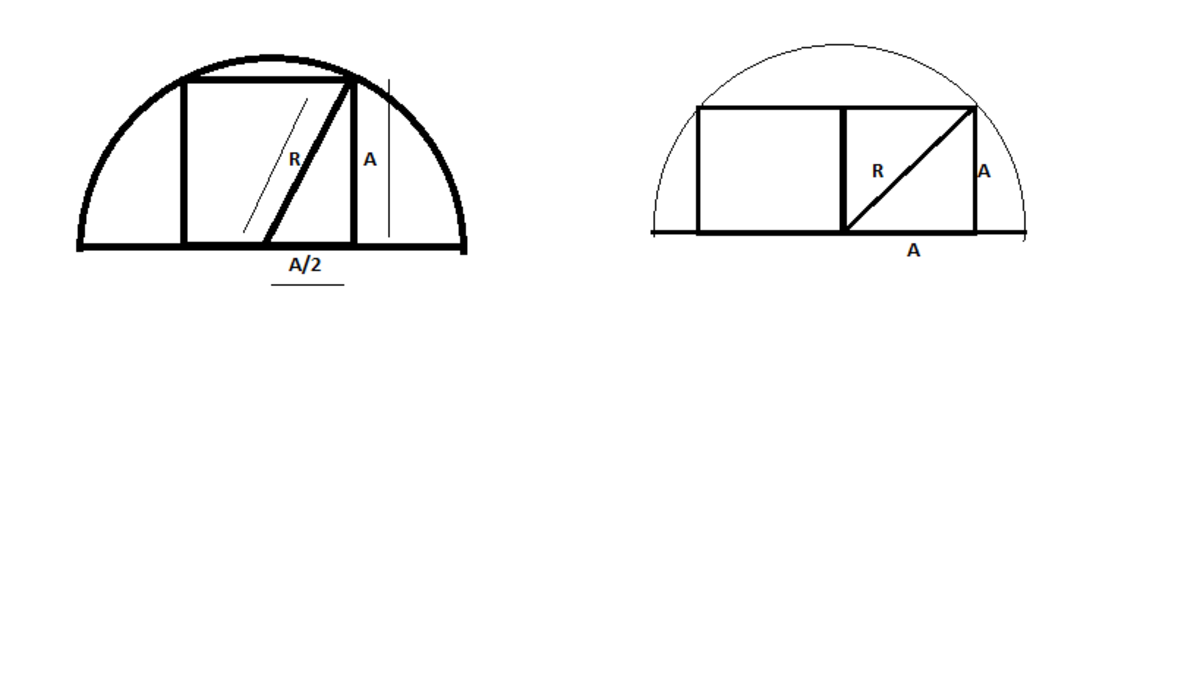 Let the angle between A/2 and R be
Θ
This gives
R
s
i
n
Θ
.
R
c
o
s
Θ
=
A
.
2
A
Multiplying by 2 on both sides gives
2
.
R
s
i
n
Θ
.
R
c
o
s
Θ
=
A
2
Let the angle between A/2 and R be
Θ
This gives
R
s
i
n
Θ
.
R
c
o
s
Θ
=
A
.
2
A
Multiplying by 2 on both sides gives
2
.
R
s
i
n
Θ
.
R
c
o
s
Θ
=
A
2
or
Area = 2 . R 2 s i n ( 2 Θ ) .
Applying Pythagoras, we get R 2 = 4 5 . A 2 substitution gives us s i n ( 2 Θ ) = 5 4 ∴ A r e a 1 = 5 4 R 2
Now the two smaller squares. From figure A . 2 = R Area of Square A 2 = 2 R 2 Area of two squares = A ′ = 2 . A 2 = R 2
Taking ratio A ′ A r e a 1 = 5 4
Is there a way to think of this by converting the trig to cartesian coordinates? I was thinking that if it is a unit circle, then the vertices of the square must be at (1/3, 2/3) and (-1/3, 2/3), while the rectangle is at (1/2, 1/2) and (-1/2, 1/2). That's not right because I got 8:9 for my ratio, not 4:5, but can you do something like that? (Forgive my rusty trig, I haven't used it since the 80s.)
Log in to reply
Assuming it a unit circle is not the correct method. However, even if u consider it a unit circle, you cannot approach it that way because the side of the square is not given, and we have only one factor, the radius that's given. I see where you are getting at, but you are missing the fact that we have to consider an arbitrary element as the side of the square. You cannot relate the side of a square directly.
I guess approaching it the Cartesian way, its going to be harder. And I just an getting used to trig in high school so I m not too good either.
Let s be the side length of the square, n be the number of the square in the circle, r be the radius of the circle.
Then,
( 2 n s ) 2 + s 2 4 n 2 + 4 s 2 s 2 = r 2 = r 2 = n 2 + 4 4 r 2
The area of the squares is n s 2 ⟹ A = n 2 + 4 4 n r 2
Putting n = 1 , A = 1 2 + 4 4 × 1 r 2 = 5 4 r 2 (green area)
Putting n = 2 , A = 2 2 + 4 4 × 2 r 2 = r 2 (blue area)
Thus, ratio of the green area to the blue area is 4 : 5
Bonus:
A = n 2 + 4 4 n r 2 = n + n 4 4 r 2
By AM-GM, we have 2 n + n 4 ≥ 4 ⟹ n + n 4 ≥ 4
Equality hold when n = 2
Hence, A is maximum when n + n 4 is minimum, which is when n = 2
Circle equation (suppose it's a unit-circle):
x 2 + y 2 = 1
Green equation (side length s G ):
( 2 s G ) 2 + s G 2 = 1 4 5 s G 2 = 1 ⟹ s G 2 = 5 4 = A G
Blue equation (side length s B ):
s B 2 + s B 2 = 1 ⟹ s B 2 = 2 1 = 2 A B ⟹ A B = 1

Proof using Pythagorean Theorem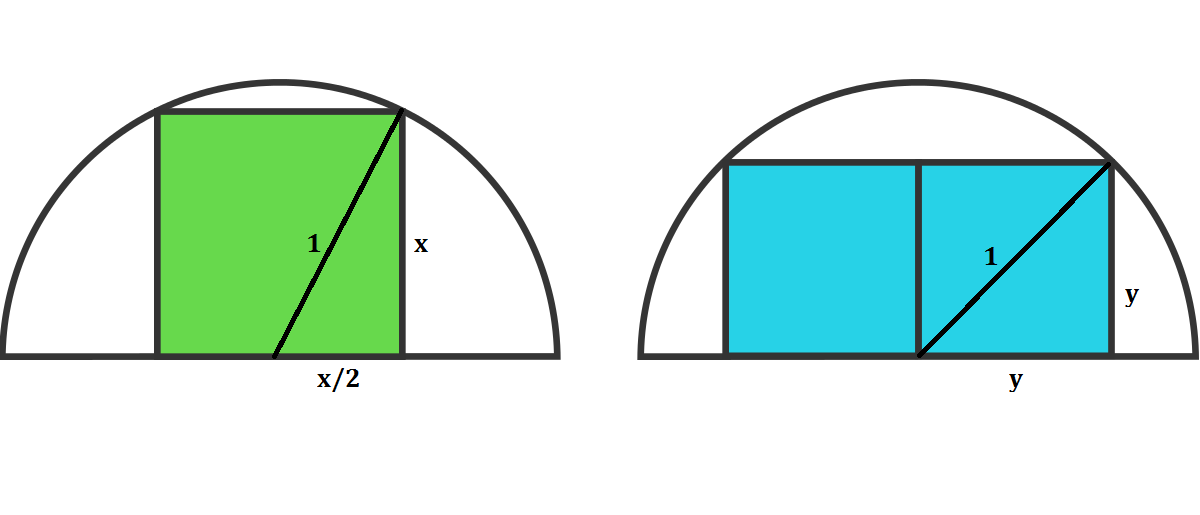
Let's assume that the circle has a radius of 1 unit.
In the first case, x 2 + 4 x 2 = 1 ⟹ x 2 = 5 4 This is the area of the green region. A g r e e n = x 2 = 5 4
In the second case, y 2 + y 2 = 1 ⟹ y 2 = 2 1 But, this is the area of half of the blue region. So, A b l u e = 2 y 2 = 1
Therefore, A b l u e A g r e e n = 5 4
Generalization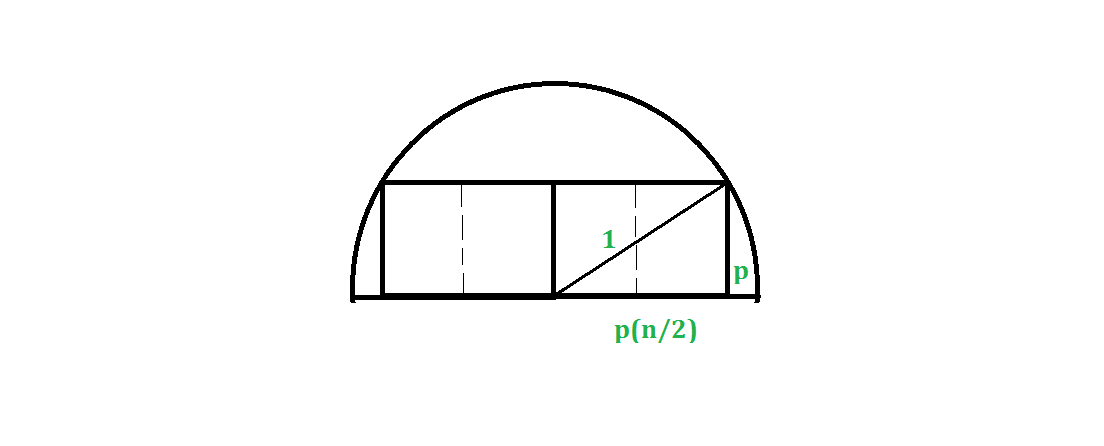
For the general case, assume p is the side length. So, from Pythagorean theorem: ( 2 p n ) 2 + p 2 = 1 ⟹ p 2 = 4 + n 2 4
Hence, the total area would be, A = n p 2 = 4 + n 2 4 n
Also, we can find the optimal value of n for getting maximum A . Just taking the derivative gives us: ( 4 + n 2 ) 2 ( 4 + n 2 ) 4 − 4 n ( 2 n ) = 0 ⟹ 1 6 + 4 n 2 − 8 n 2 = 0 ⟹ n = 2
So, n = 2 corresponds to the max area attainable. Another way to look at it is to add a mirror image.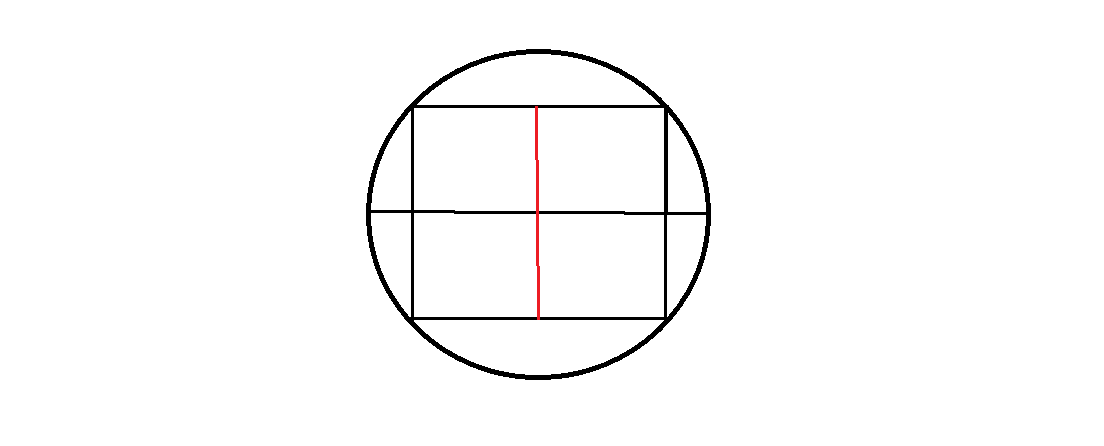 We can see that
n
=
2
is actually a cut-down version of a square inscribed in a circle. So, it must correspond to the max area.
We can see that
n
=
2
is actually a cut-down version of a square inscribed in a circle. So, it must correspond to the max area.