85 of 100: Tic Tac Sabotage
What is the least number of unit squares that you need to remove from this 5 by 3 checker board in order to make it impossible for anyone to put an "X" in 3 remaining squares to make a connected vertical, horizontal, or diagonal set of 3 (a set that looks like a "win" in a standard Tic Tac Toe game)?
Hint: Try the problem on a smaller board first.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
This shows 6 (or m+floor(m/3)) is an upper bound but I don't see how it shows 5 is impossible
Log in to reply
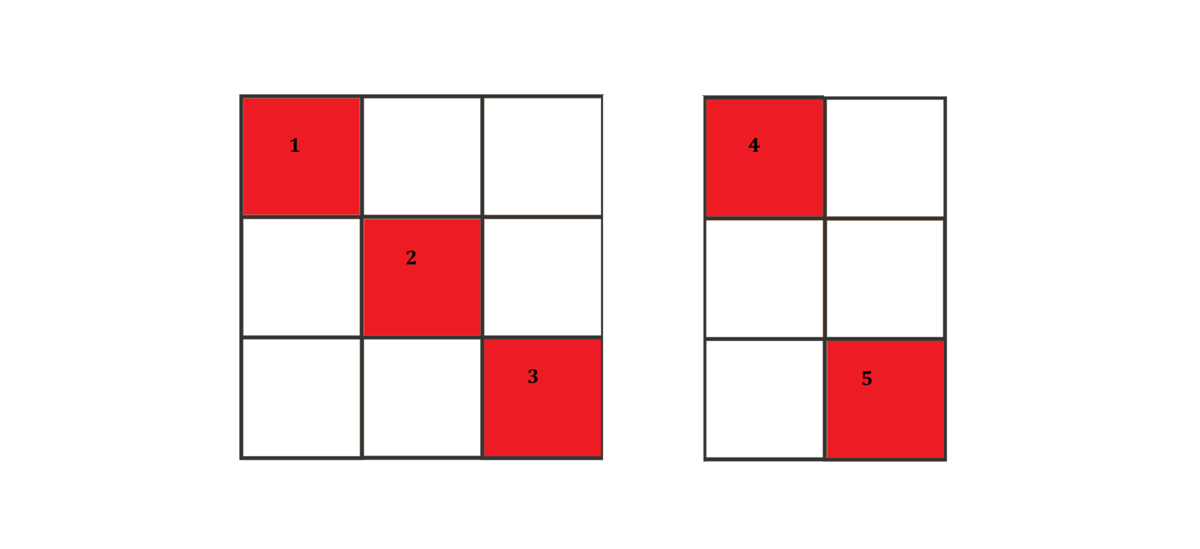
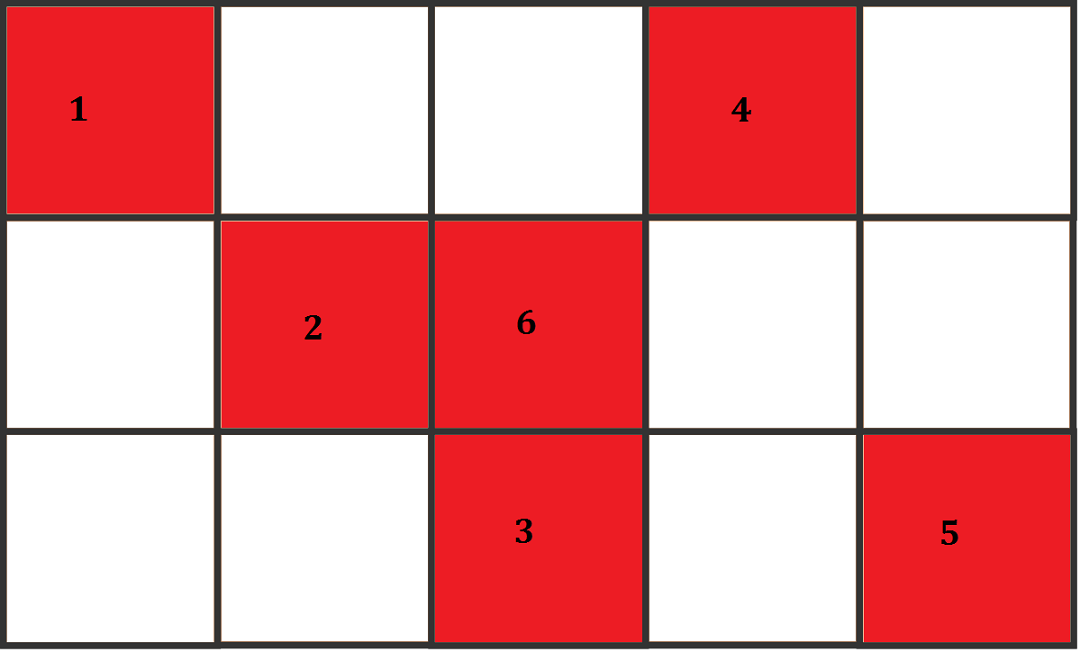
Let's think about it this way. We'll first block all the winning lines in a 3 × 3 and a 3 × 2 tic-tac-toe. Then, we'll try to concatenate them. You will see that it's sufficient to block the winning lines of these 2 tic-tac-toes individually with 5 removals. But, when concatenated together, new winning lines emerge. So, we need another square removed.
It's much harder to generalize to an algorithm for finding the minimum squares that need to be removed in an m × n rectangle. The largest connected polyominoes that are allowed to remain are two different tetraminoes, the 2 × 2 square, and the Z-shaped tetramino. These can be tiled in various ways.
Log in to reply
Are you assuming that the winning lines consist of 3 adjacent squares whose centers lie in a straight line? Then, generalizing it would be hard. I have another thing in my mind. If we define winning lines as m i n ( m , n ) numbers of squares lying in a straight line then, it would be easier. We can remove the diagonal squares which immediately eliminate many winning lines.
Log in to reply
I am assuming that no connected vertical, horizontal, or diagonal sets of 3 squares should remain, as in the wording of the problem. I was playing with the limiting case, in which the rectangle grows without bounds in both dimensions. In that case, I am convinced that the portion of the tiles that must be removed approaches 2 1 of the total number of tiles in the plane as the limit.
I published one idea on how to generalize to an "infinite" checkerboard as a separate solution below, so I could post a picture of an example array. Take a look at it, and see what you think!
I just checked your generalization for the 3 × m rectangles, and it is incorrect. If m = 3 n and n > 1 , then the minimum number to remove is, I believe, 4 n . If m = 3 n + 1 , then the number is 4 n + 1 . If m = 3 n + 2 , the number is 4 n + 2 .
Log in to reply
It's m ≥ 3 in my case. Also, if m = 3 and I substitute it in m = 3 n and 9 4 n then, I get 9 4 . How is that possible? Again, take m = 6 and n = 2 , then the min number of square is 9 8 ???
Log in to reply
Sorry, I've edited my comment. I had interchanged m and n in a crucial place. Try re-reading it now. For example, if m = 9 , so that n = 3 , you can get away with removing only 4 ( 3 ) = 1 2 squares, not 5 ( 3 ) − 2 = 1 3 squares.
My generalization can be incorrect. It's only a claim. But, the generalization you provided is not making any sense to me! Can you explain your formulae in detail?
Log in to reply
It's based on the idea that for a rectangle with 3 rows and 3 n columns, you have to remove two squares from every third column, and can remove one square from all the other columns. This works out to be 4 squares out of every 3 columns, or 4 of every 9 squares. In the special case of a 3 × 3 rectangle, you can get away with only removing one square from each column. Try it!
Log in to reply
@Mark Lama – I see the pattern now. Thanks for generalizing it. I'll edit my solution to give the correct formulae.
Log in to reply
@Atomsky Jahid – This is a comedy of errors on my part! Wherever I said 9 4 n , replace it with 4 n . Sorry, it's late here, and I am tired!
@Mark Lama , please check if it's correct this time.
Log in to reply
Nice! I like the use of the floor function to simplify things. The only thing that needs to be clarified is that m = 3 is a special case, in which the function you give does not hold.
Log in to reply
Actually, 3 + ⌊ 3 3 ⌋ = 3 + 1 = 4 which serves our purpose.
Log in to reply
@Atomsky Jahid – But it is not the minimum! For a 3 × 3 rectangle, you only have to remove 3 squares, not 4.
Log in to reply
@Mark Lama – Oops! I forgot my original images totally. -_-
I think I see my problem; it was sufficient to block any 3 length number of x's, as a win, for instance, horizontal, even though it was not imbedded in a normal 3x3 tic-tac-toe construction. I find the problem wording confusing, but think I know what I didn't know. Ed Gray
I guess I don't understand the problem. If we remove the 5 squares consisting of the first row, we are left with a 2 x 5 matrix. But tic-tac-toe requires a 3 x 3 matrix, which would be impossible; so I will stay with 5. Ed Gray
In every column there has to be at least 1 unit square removed, because otherwise that specific column gives the opportunity to put three X's in it. So at least 5 unit squares must be removed. But is it possible with only 5?
If you start removing 1 unit square from the first column and 1 unit square from the second column then there are two options. They are in the same row or they are not. 1) If they are in the same row then from the third column there has to be removed 2 unit squares, namely the 2 unit squares from the other two rows. 2) If they are not in the same row then it's more complicated. It depends on which unit square you have removed from the first column and also the second column. Below you see a picture of the (basically) three different options. The green unit squares are the ones you choose and the red unit squares are the ones necessary (depends on what you have chosen).
 So you see that sooner or later there have to be 2 unit squares removed from one column. The conclusion is that it's not possible with only 5 unit squares removed. Is it possible with 6 then? Yes.
So you see that sooner or later there have to be 2 unit squares removed from one column. The conclusion is that it's not possible with only 5 unit squares removed. Is it possible with 6 then? Yes.

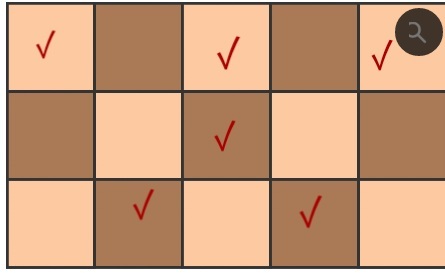
At first, we have to remove at least one square from each of 5 columns,.
so that, no 3 squares can be joined vertically.
THIS PROCESS MUST BE DONE IN SUCH WAY, SO THAT NO 3 SQUARES CAN BE JOINED DIAGONALLY.
As shown in the figure,
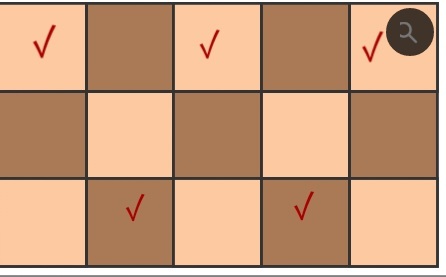 now, after this process, there is a possibility to join 3 squares horizontally in the middle row.
now, after this process, there is a possibility to join 3 squares horizontally in the middle row.
So to avoid this situation, we have to remove the middle most square of the middle row.
Hence, minimum number of removed squares is=(5+1)=6
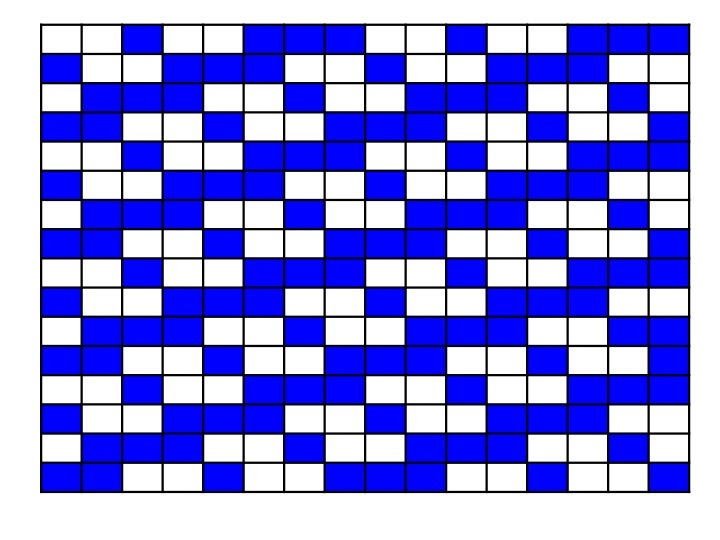
As the 3 × 5 case has been well answered, I'd like to look at the limiting case, where the rectangle grows in both dimensions without bounds. What is the lower bound of the ratio of the total squares that have to be removed so that no connected horizontal, vertical, or diagonal sets of three squares remain? I would maintain that the minimum ratio approaches 2 1 . Consider the following 1 6 × 1 6 array that illustrates what I believe to be the closest packed tiling of allowed squares. Allowed squares are white; squares that must be removed are blue. Clearly, in each row, half of the squares are being removed. Again, in each column, clearly half of the squares are being removed. I challenge you to find a closer packing!
I was working on two things. 1. n × n squares where winning lines consist of n adjacent squares which lie in a straight line. 2. 3 n × 3 n where winning lines consist of 3 adjacent squares.
In the case of (1), we need to remove n squares when n is odd OR we need to remove n + 1 squares when n is even. As you can tell the fractions n 2 n and n 2 n + 1 both approaches 0 when n grows without bound.
In the case of (2), I worked with 6 × 6 , 9 × 9 and so on. The fraction of squares that need to be removed turns out to be close to 2 1 . I got fractions like 9 4 , 2 7 1 3 etc. So, I speculated it will eventually converge to 2 1 . But, my removal approach is different than yours. I essentially worked with diagonal squares.
Currently, I am pressed for time as I have exams going on. But, If I can, I will upload my approach with the fraction of squares that need to be removed as a closed form.
Log in to reply
No problem! I am also studying for an exam in two days.
My diagonal approach ends up with a fraction removal of 9 5 − 9 n 2 . I have told you before that it approaches one-half. But, I was wrong. It approaches 9 5 .
On the other hand, your z-tetromino approaches 2 1 . Ummm....
I took a second look at your approach. It seems like z-tetromino method gives precisely 2 1 for m × m arrays.
Log in to reply
I also examined a tiling of 2 × 2 square tetraminoes, where the ratio of removed squares does approach 9 5 , although in smaller cases, it can give a much lower ratio, such as in the 5 × 5 square, where using four of these squares gives a removed/total ratio of 2 5 9 . I would not be at all surprised if other packings existed that yielded a limit of 2 1 . What would surprise me is if a legal packing existed that yielded a limit lower than 2 1 . My challenge was to create a pattern that was infinitely repeatable, so that it could be easily analyzed.
I. Six boxes is possible.
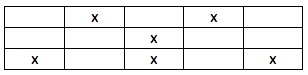
But for a complete answer, we must prove that less than six is not possible.
II. To prevent a win, we need to remove at least one box in every column . Clearly, that requires a minimum of five boxes .
III. Moreover, in each row we must remove at least
-
either the middle box
-
or two boxes, but not on opposite edges.
The only way to do this with five boxes is as follows:
-
remove box 3 (the middle box) from any row;
-
remove boxes 1 and 4 from another row;
-
remove boxes 2 and 5 from the remaining row.
IV. However, we must also take care of the six "long diagonal" (i.e. of three boxes in a row). Diagonals in opposite directions overlap, so in principle it seems possible to do this by removing five boxes. However, it is impossible! To see this, consider that steps II and III above leave essentially two different situations (up to mirror image):

In either case, there are two winning diagonals. It is therefore not possible to do it with five boxes.
As many solved correctly, there is a solution with 6 removals looking thus:
where X is a removal.
Can we prove that it's minimal? Easy enough, it follows from the pigeonhole principle that the minimal number is at least 5 (one removal for each column). Lets assume that there's a solution with 5 removals. As said before, each removal will occur at a distinct column, so we're covered with the columns, and left with rows and diagonals.
Without loss of generality, lets give values to columns:
So we can represent the board with a ternary sequence with length 5.
For example, a board looking thus:
will be represented by the sequence 02101. While it's not necessary to use a new representation, it makes life easier.
To make a winning row impossible, we need no horizontally consecutive 3 rows without any removal. In our new representation, it means that all the three subsequences of length 3 should be made of all 3 digits. For example, let's look at the previous example board 02101. It's subsequences are 021, 210, 101. The two first meet that criterion, but the third does not, as 2 is not there. It means that there are 3 legal places in the end of the bottom row, and you can see that there is a legal win there (Three empty places in a row). Assume we want to build a board blocking all the rows. If we choose two different digits at the beginning (they must be different otherwise the first subsequence won't meet our criterion), the third digit must be the one we haven't used. Looking at the second subsequence, we see that the fourth digit must be the first one, and likewise looking at the 3rd subsequence the 5th digit is the second one. We really find here that our pattern must be periodic, and is determined by the first two digits.
For example, let's start the sequence with 02: 02???. The next one must be 1, looking at the subsequence 02?. So now we have 021??. Looking at the next subsequence 21?, we see it must be zero. Now we have 0210?, and make sure you understand why the last digit is 2.
So the two first digits determine the others, leaving us with 6 different boards: 01201,12012, 20120, 21021, 10210, 02102. They look very similar, right? You can imagine what will it look like for a 3xN board - it'll just go periodically like that forever.
Now lets talk about diagonals. A board is free of diagonal wins if any 3-subsequence shares at least one common digit with the sequences 012 and 210. In our earlier example, 02101, 210 has no common digit with the subsequence 021, thus it allows a diagonal win from bottom left to the right.
It can be seen that all possible 6 boards allow such diagonals, as they all contain a subsequence of the kind 021 or 201. Thus, It's impossible to use only 5 removals and so 6 is the minimum.
Q.E.D.
**One of the solutions I thought was this one.
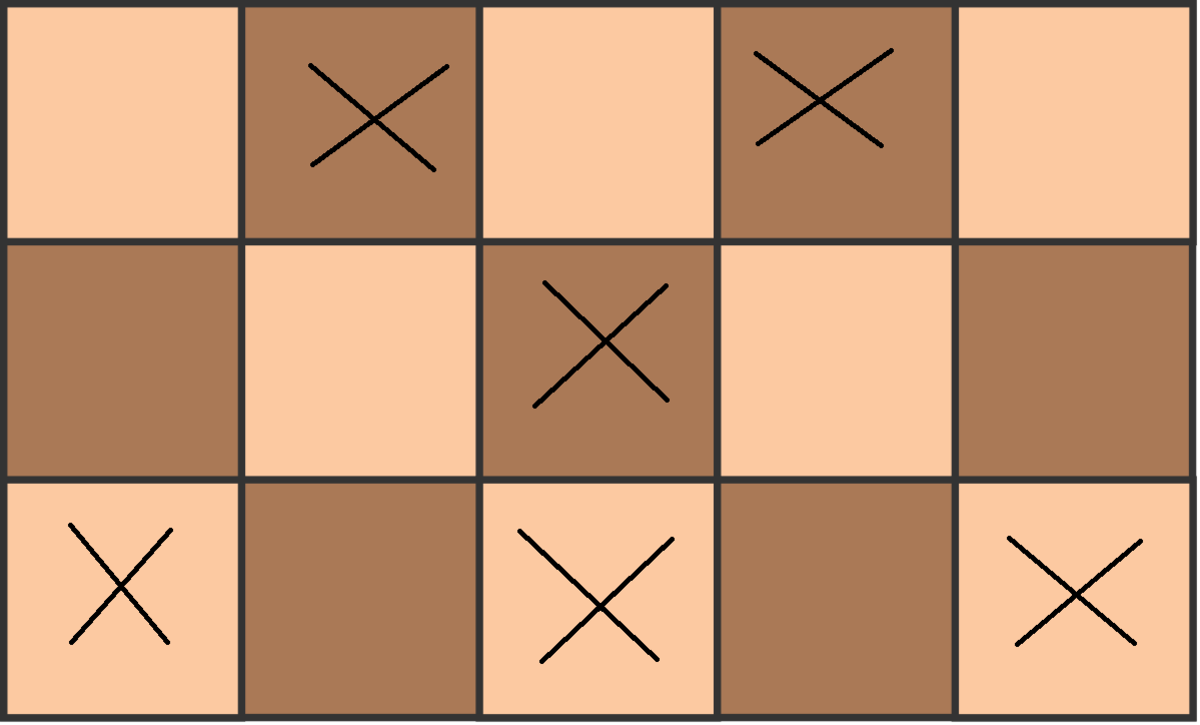 This prevents any 3 in a row possibilites.
This prevents any 3 in a row possibilites.
Why 5 doesn't work: Let's remove 5 squares so that 3 in a row will be impossible horizontally or vertically, then prove that we can get 3 in a row diagonally.
As others observed, each column would only have one square removed. At least one row will have no more than one square removed. In that row the middle square has to be removed. That can only happen in one row, so other two rows will have to have each 2 squares removed. The square removed from the first column is in a row that needs another square removed so it's not the middle one, because that's in the row that only had one square removed. It can therefore only be the 4th square.
That means one row has squares 1 and 4 removed, one squares 2 and 5, and one just square 3. We'll put the first X into the square 3 of a row that is touching the row with square 3 removed (so either just below or just above the removed square in the middle column). If that removed square is in the middle row we do (1) otherwise we do (2).
(1) Let's put X into the middle of the top row. In the bottom row another X has to go into square 1 or 5, one of them is available because they haven't been both removed. If it's in square 1, we put the final X in the middle row in square 2. If 5 then 4. Both 2 and 4 are available in the middle row because only square 3 has been removed.
(2) The X must be In the middle row. In the other row with 2 squares removed either square 2 or square 4 has not been removed, we put the second X there. 3 in a diagonal will then be complete by putting the third X into the row where just the square 3 has been removed. It will have to go either into square 2 or into square 4 (opposite from the second X), which are both available because only square 3 has been removed.
See Tic Tac Toe Warmup in Logic > Deterministic Games.


First, remove one square (colored red in this image) per column. Remove them in a zigzag fashion. Then, remove another square (colored purple) from row #2. It should take 6 removed squares to block any winning line.
Generalization
Let's say we have a 3 × m tic-tac-toe. Now, we are trying to generalize the minimum number of squares that need to be removed.
C l a i m :
For a 3 × 3 tic-tac-toe, only 3 squares need to be removed. And, for a 3 × m tic-tac-toe (where m = 3 ), the number of squares that need to be removed is m + ⌊ 3 m ⌋
The idea goes like this:
For m = 3 , removing the diagonals is optimal. For m = 3 , the following process turns out to be good enough.
For every column, we need to remove 1 square. These are colored in red. So, m red squares are removed. Also, we need to remove 1 square from every 3 squares in row #2. These are colored in purple. Number of purple squares is ⌊ 3 m ⌋ . Therefore, we need to remove m + ⌊ 3 m ⌋ squares in total.
[Thanks goes to @Mark Lama for helping me in this.]