9 of 100: Bond. James Bond.
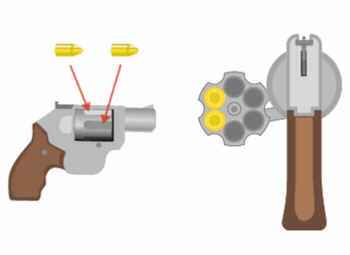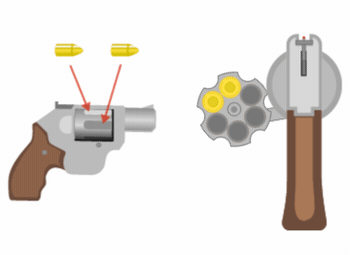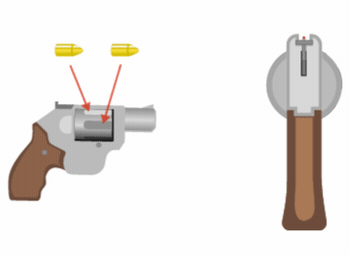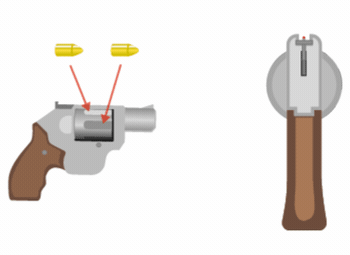
Agent Bond has been captured and is about to be killed by his enemy, Scaramanga. Scaramanga takes a six-chamber revolver and places two bullets next to one another, as shown above. He spins and locks the cylinder so a random chamber is on top, aims at Bond, and fires ... nothing happens. He then tells Bond that he will fire once more and if Bond is still standing afterwards he is free to go.
Scaramanga gives Bond two options − either he fires again right away or spins the cylinder of the revolver so a random chamber is on top and then fires. Which option makes it more likely that agent Bond will survive?
Note: After firing, a gun automatically rotates the cylinder by one position to fire from the next chamber over.
For this problem, assume that Bond is out of tricks and that he must make this choice carefully to maximize his chances of survival.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
Nice explanation. Just wondering, if instead of bullets being placed one after other, they were placed having one vacant position between them. Then the probability of next shot being fired (after one miss) would be 2/4 = 1/2. in this scenario, other option seems to be correct. Now imagine if the two bullets were placed randomly, then what will be the probability of next miss(or next hit)?
I got this wrong because I read the question wrong. I assumed the two consecutive shots vs the shot spin shot option were before the shots were taken. This leads to the opposite strategy being preferred.
Consecutive shots: 4/6 x 3/5 =12/30 = 40%
(If we use 3/4 not 3/5 its 50%)
Shot spin shot : 4/6 x 4/6 = 16/36 =50%
Sorry James, I failed you. :/
This is the exact same reasoning that I used to solve this.
How does this relate to the Monty Hall problem? Is it not related to that?
Log in to reply
Both involve conditional Probability
This is not a Monty Hall variant. That requires a "host" that knows about where something is, and does some action accordingly. Both spins are random here where the shooter doesn't know where the bullets are relative to the chamber.
O cenário apresentado é o que apresenta a melhor possibilidade de vida. No entanto, existe uma condição ruim: Imagine que o primeiro tiro foi na câmara 4. Assim, o próximo tiro será a morte. Nâo dá pra saber. Só por isso, 2/3 em um novo giro é melhor.
The scenario presented is what represents the best possibility of life among all possible. However, there is a bad condition: Imagine that the first shot was in chamber 4. So the next shot will be death. It's impossible to know. That's why 2/3 in a new spin is better.
What if "nothing happened" because it was a misfire? Would it become a 2/5 probability of being shot if he fired right away?
Log in to reply
One half, I believe.
I also thought that way
Log in to reply
As in: I thought if the guy was to shoot right away, the probability that Bond dies is 2/5
guys you need to consider gravity when spinning... because of it the bullets will position themselves on the bottom of your revolver...:)
YA .
Very true.
But think you are given this scenario and someone is holding gun in front of you.
Then all these cannot come in our brain
We will be in Panic.
isnt it?
Can you think that time also?
Log in to reply
Lol! My friend, you must remember: Don't panic!
Log in to reply
Haha, Very true. But panic is not such a thing which we can hold on, It will come up when we see guns in front of us.
At that time, reasoning something is quite tough.
Log in to reply
@Md Zuhair – Yes, but for James Bond 007, this is just another day at the office.
Log in to reply
@Steven Chase – Ya, Lol! Very true sir!
Steven Sir, Can i have your email please?
I want to clear some doubts.
You can also provide your phone number through email
And if you are feeling insecure to give up your email
here is myne
Log in to reply
@Md Zuhair – Could you PM me on slack instead?

First, we will calculate the probability of spinning and shooting. If Bond chooses to spin and shoot, there is a 6 4 = 3 2 chance he will survive, as 4 out of 6 chambers are empty.
But if Bond chooses to shoot without spinning, there are 5 chambers left, so one would think there would be only a 5 3 chance of survival. But since the two bullets are next to each other, Bullet B cannot be shot out of the gun, since it can only be fired after Bullet A has been fired. Therefore, there is a 4 3 chance of survival if Bond chooses to shoot without spinning, due to the fact that the two bullets are next to each other and that Bullet B cannot be the one that is fired.
Since a 4 3 chance of survival is better than a 3 2 one, Bond should choose to shoot without spinning.
If two bullets were placed randomly, then spin and fire would have been better strategy, am I right?
Log in to reply
Right, in this case we can imagine the bullets got placed after the initial empty chamber. Then there would be a 2/5 chance of hitting a live bullet at the next shot.
Spinning would be a 2/6 chance, so that would be the better option here.
Siva, If we label the chambers 1-6 and say the bullets were in 5/6 then they are both eliminated from the possible starting points for the initial shot. Therefore, we only have 4 possibilities at hand (landing in 1-4). Landing initially in chambers 1-3 allow Bond to survive and chamber 4 is the only option where he dies. This means we actually have a 3/4 chance of surviving if we shoot twice in a row instead of a 2/3 chance of random spinning again. Still better chances but not 4/5.
Log in to reply
Sorry, that was just a brain fart on my part. I have changed it.
But if you load two bullets next to each other, the weight will cause the loaded bullets to be at the bottom after the spin.
Log in to reply
The problem states specifically that a "random chamber" will be on top. This means 1 out of the 6 at random, not according to any physics.
I don't think that what was the problem was intended to be interpreted as.
I'm a bit unsure about the probabilities. First, the probability that he survives if he carries on is 3/4. I'm confident about that, because 3 out of 4 slots will mean the next slot is empty as well. However, to calculate the probability he survives by spinning, why is it not 1/4 (the probability of the next slot having a bullet before spinning) multiplied by 2/3 (the probability of not ending up on a bullet after the spin) = 1/6? Why do we not combine the two probabilities? Surely the chance of him surviving after a spin means he has to spin in the first place, which takes into account the 1/4 chance that a spin is necessary.
Log in to reply
We don't care about the probability before spinning. All that matters is the probability after spinning, which is 4/6 = 2/3.
Log in to reply
I don't understand why we don't need the probability before spinning, because to get to this position he would need to spin in the first place, which has a probability of its own (1/4).
this is the best answer as i feel. Thanks.. !! i was messed up in wrong direction. :)
If you don't spin after pulling the trigger on an empty chamber, your chances are down to 3 empty and 2 with bullets. If you spin, then you're back to 4 empty and 2 with bullets, period. Nothing you say can tell me that pulling the trigger again with no spin is a better solution.
Log in to reply
Well, there is a crowd that still insists the Monty Hall thing is 50/50. The same goes for a certain dice problem that is either 1/11 or 2/11 depending on slightly different conditions but the crowd insists its still 1/6. And there are flat earthers. All about the same. Can't convince any of them either.
Incorrect. The weight of the bullets makes it unlikely for the bullets to be on the top, where the hammer is.
By not firing on the first pull of the trigger, one of the empty chambers has been eliminated, leaving Bond with 3 empty chambers and two loaded, a 3/5 or 60% chance of survival. A spin would put him back at 2/3 or 66.7% chance. Spin away!
Log in to reply
It doesn't work like this. When the first shot is fired you can't assume that the next one would be a random one of the ones not fired. From the way they are distributed in the chambers, you can figure out that if the first shot was an empty chamber, then the chance that the one in the clockwise chamber is empty is 3/4, as 3/4 of the empty chambers have an empty clockwise chamber.
Log in to reply
You're correct. I neglected to take into account the second loaded chamber is also eliminated after the first pull of the trigger.
it is not 3/5.. u can not consider the position with second slot empty when first had the bullet.. bond wd not survive in the first place to check this particular branch of probability.
make a tree in mind and be careful about which branch leads to what final event. that may help.
Once a blank is fired, (knowing that angular movement has unchangeable direction) there are four possibilities for the next chamber:
-
first possibility is that there is a bullet in it, and
-
other three that there is a blank.
Hence, the probability of finding the bullet is 4 1 , implying that Bond has 4 3 chances to survive. If he chooses to spin, then he has the same chances of surviving like he had at the beginning: 3 2 . It's clear that, in order to increase his chances of survival, he should choose Scaramanga to shoot right away!
Good explanation, but I don't think "angular momentum" is really involved, rather that's just the mechanism of the revolver.
Log in to reply
Thank you! I wrote movement, not momentum. I was referring to unchangeable spin direction of the revolver.
Log in to reply
Whoops! Must have read it too fast.
If Scaramanga spins again then the probability that a bullet will be fired is 2 (bullets)/6 (chambers) = 1/3. If he fires straight away then IT SEEMS TO ME that the bullets could have been in chambers (1 & 2) - but this must be eliminated as a possibility because that would mean that Bond would already have been killed with a bullet from the 1st chamber. But the other possibilities are (2 & 3), (3 & 4), (4 & 5) or (5 & 6) each with equal probabilities which add up to 1, so each with 1/4. And with only the 1st one of these does Bond die with the bullets been in chambers 2 & 3. So the probability is less (1/4) if Scaramanga fires immediately! Regards, David Ps If the bullets were not next to each other then the prob of death if just firing would be the number of bullets (2) divided by the number of chambers OTHER THAN THE 1ST ONE which we know was blank, AND HAS ALREADY GONE. So that is 5. So the prob of death would be 2/5 which is more than 1/3.
Let's translate this into an analysis of the possible scenarios 0a 0b 0c 1x 1y 0d Imagine each term as an cylinder, when it has 0 theres not bullet inside, when it has 1 there is a bullet Possible scenarios:
[0a 0b], [0b 0c], [0c 1x], [1x 1y], [1y 0d], [0d 0a]
Remember that when he shoot first time there wasn't any bullet, let's take the cases where he shoots nothing happens and when he shoots again James die. [ 0c 1x] Unique case from all the 6 possibilities, so the chance is 6 1
taking the possible scenarios already "drawn" again let's analise the chances of a first try bullet when he spins the cylinder. [1x 1y], [1y 0d], 2 out of 6, 3 1 , with all those informations we can conclude that the chance of a first try bullet is greater than a sequence of "Nothing happens, boom".
This was my same idea to solve this quiz, you die at the second shot only if the first shot was a blank beside the bullet. So it is 1/6 chance vs 2/6 if we reroll at second shot.
We know that 2 out of 6 chambers are filled, meaning that the random, spun chance of Bond's death is 6 2 , this carries out no matter when it is spun, as long as the chances are truly random, and not selected by Scaramanga. From the given information of the first shot containing no bullet, we can deduce, because a revolver only spins in one direction, and the bullets are next to each other; not spread out, that the chance of the next shot containing a bullet is only 4 1 because only 1 of the 4 empty chambers allows the next shot to be fatal. When the two fractions are multiplied to have the same denominator, such as 12, the chance of death on spun = 1 2 4 , and the chance of death on shoot = 1 2 3 , therefore the chance of Bond's death is larger in case of a randomly spun cylinder.
A random spin gives the chance of 6 2 , or a third. If the next shot is fired, there are only five possibilities left, but you know that the second bullet won't be fired, as they are next to each other, so it is one in five
- If Scaramanga spins the cylinder so that a random chamber is on top, then there's a probability of 2 / 5 that this chamber contains a bullet.
-
Else, if Scaramanga intends to fires again right away, then:
- as we know for sure that the current chamber is an empty one
- and since, among the 4 empty chambers, only one has a succeeding chamber containing a bullet
the probability for the next chamber - from which Scaramanga will fire - to contain a bullet is 1 / 4 ( < 2 / 5 ).
Therefore, Bond had better have Scaramanga fire right away.
The number of chambers did not decrease when scaramanga fired the first time, meaning the random spin results in a probability of 2/6, not 2/5.
Similar to Monty Hall problem
How did such a big percentage of people fail? If he is going to be killed because the bullet is above and Scaramanga spins he is going to be killed anyway (as both of the bullets are one nexto to the other. Nevertheless, if he isn't going to be killed because the bullet is not above, by spining the cylinder the buller might be in the next position so it's positioned above and kills Agent Bond. I hope u've understood, I'm not english, but spanish haha.
Why you guys make it so complicated?.. Probability of the next chamber having a bullet is 1/6. Probability of the chamber having a bullet if you spin again is 2/6.
So my original idea was correct? (the same as heare 1/6 chance to die the second shot vs 2/6 with reroll)
If you spin the chamber, there is a higher chance for Agent Bond to be killed. If you just fire, there's a lower probability for Bond to be shot.
Please go into more detail when posting solutions. Why is the probability lower when you just fire?
Log in to reply
Hey, I'm just an 11-year-old kid. I can have simple or complex reasons. It's my choice.
This is simple yet complex. For the first shot, we know that it could have been from one of the four chambers without a bullet. We know that with only one of the chambers the next shot would be a bullet. So if Bond chooses to just fire, his chances of surviving are 4 3 . 2 out of the 6 chambers, or 3 1 of the chambers, have a bullet in them. This means that there is a 3 1 chance of spinning and getting a bullet. So, if Bond chooses to spin, then fire, his chances of surviving are 3 2 . 4 3 is greater than 3 2 , so Bond has a greater chance of surviving if he chooses to just fire .
I wrote this for people who prefer a written solution over visual, I apologize for any math mistakes I might have made( I'm only 11 ). : )
Before firing, there are 2/6 positions that are lethal. Survival chances are 2/3. Firing a blank limits the available orientations to 4 only, one of which can result in a lethal strike, with odds of survival at 3/4. So the odds are: a) spin again (2/3 odds of survival) and b) fire a consecutive time (3/4 odds of survival). Bond should instruct Scaramanga to pull the trigger a second time.
When there is a random shot chosen, 4 out of 6 of the choices will result in Bond surviving, a 3 2 chance. We are given that Scaramanga already fired an empty barrel. If the empty barrel is next to a barrel with a shot in it and Bond just wanted Scaramanga to fire the next shot, he would die. There is one empty barrel which is before a barrel with a shot in it, out of 4 barrels. Therefore, the chance of surviving when firing the next shot is 4 3 . 4 3 > 3 2 , so Bond has a greater chance of surviving if he tells Scaramanga to fire the next shot.
Just think that in other way You have 6 pen ,2 are good and 4 defective U take a pen and it comes out to be defective, U throw it away now u have 2 good 3 bad pens so u have more probability to pick good pen than again repeating the procedure
If Bond rotates and then fires, the probability of shooting a bullet is 2/6 = 1/3. In this case Bond has a 2/3 chance of surviving.
When Scaramanga pulled the trigger on an empty chamber, there is a 1/4 chance that the next chamber has a bullet. So there is a 3/4 chance of surviving since most empty chambers are next to other empty chambers. Bond's best option is to just pull the trigger.
If we spin the slot the probability for James to be not shot is 2/3. But if we know that the chamber that will be selected is the next of one of the empty chambers, then the probability is 3/4 for James to survive. Is better for him the first option.

The revolver carousel spins in the same direction each time. I have arbitrarily chosen a counter-clockwise convention. I have numbered the empty chambers from 1 to 4. Here are the scenarios:
Chamber 1: Next chamber is a kill
Chamber 2: Next chamber is safe
Chamber 3: Next chamber is safe
Chamber 4: Next chamber is safe
So the probability of Bond dying if Scaramanga simply fires again is 4 1 . If Scaramanga rotates the chamber randomly before firing again, the chance of the carousel landing on a loaded chamber is 6 2 = 3 1 . Therefore, Bond is better off having Scaramanga fire the second shot straight away.