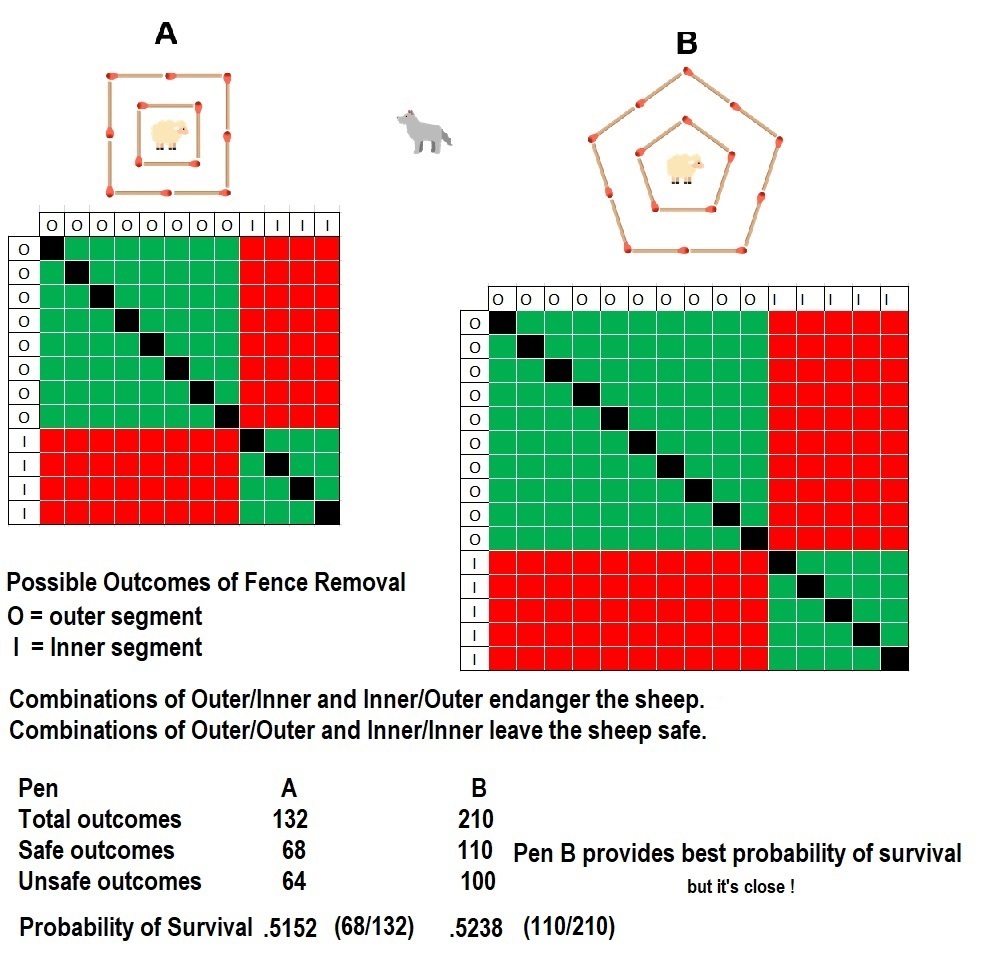
90 of 100: The Safer Sheep

Here is a quick generalization. If we have an $n$ sided polygon, the probability of the sheep not surviving is the probability that a matchstick is picked from the outer side then the inner side or the inner side then the outer side, thus we have it is

$\frac{2*(n*2n)}{3n(3n-1)} = \frac{4}{9-\frac{3}{n}}$

It is clear that for bigger $n$ , this probability gets smaller as the probability approaches $\frac{4}{9}$ from above. So, the more sides, the less likely for the sheep to die and the more likely for it to survive.

One have to remove 1 stick from outer fence in each case. So, it remains 11 and 14 sticks in total. For case 1, probability of inner stick to be chosen= 4/11

For case 2, probability of inner stick to be chosen= 5/14

4/11 > 5/14 . So, case 1 has more chance for inner stick to be chosen. Once an inner stick is chosen, it is no more safe. So, case 2 in more likely to survive.

As stated, a sheep survives if and only if both matchsticks are removed from the same (outer or inner) fence .

Sheep A : The outer fence has 8 matchsticks and the inner fence has 4 matchsticks.

P(Sheep A survives) = 1 * P(Both matchsticks are removed from the outer fence) + 1 * P(Both matchsticks are removed from the inner fence) + 0 * P(The two fences have one matchstick each removed from them).

= 1 * $\frac{{8 \choose 2}{4 \choose 0}}{12 \choose 2}$ + 1 * $\frac{{8 \choose 0}{4 \choose 2}}{12 \choose 2}$ + 0 * $\frac{{8 \choose 1}{4 \choose 1}}{12 \choose 2}$

= 1 * ( $\frac{8!}{2!*(8-2)!}$ / $\frac{12!}{2!*(12-2)!}$ ) + 1 * ( $\frac{4!}{2!*(4-2)!}$ / $\frac{12!}{2!*(12-2)!}$ )

= 1 * $\frac{28}{66}$ + 1 * $\frac{6}{66}$ = $\frac{17}{33}$ = 0.5152 .

Sheep B : Likewise, the outer fence has 10 matchsticks and the inner fence has 5 matchsticks.

P(Sheep B survives) = 1 * $\frac{{10 \choose 2}{5 \choose 0}}{15 \choose 2}$ + 1 * $\frac{{10 \choose 0}{5 \choose 2}}{15 \choose 2}$ + 0 * $\frac{{10 \choose 1}{5 \choose 1}}{15 \choose 2}$

= 1 * ( $\frac{10!}{2!*(10-2)!}$ / $\frac{15!}{2!*(15-2)!}$ ) + 1 * ( $\frac{5!}{2!*(5-2)!}$ / $\frac{15!}{2!*(15-2)!}$ )

= 1 * $\frac{45}{105}$ + 1 * $\frac{10}{105}$ = $\frac{11}{21}$ = 0.5238 .

Therefore, 0.5238 > 0.5152 which means sheep $\boxed{B}$ is more likely to survive.

Chance for sheep A to die = 8/12 x 4/11 + 4/12 x 8/11 = 48.485%

Chance for sheep B to die = 10/15 x 5/14 + 5/15 x 10/14 = 47.619%

=> Sheep A more likely to die

=> Sheep B more likely to survive

For a sheep NOT to survive there has to be removed one match from the outer fence and one match from the inner fence. For sheep A there are 8 matches on the outer fence and 4 on the inner fence, so that's a total of 12. The chance for removing one of each fence is (2)x(8/12)x(4/11)=(64/132)=(16/33). For sheep B there are 10 matches on the outer fence and 5 on the inner fence, so that's a total of 15. The chance for removing one of each fence is (2)x(10/15)x(5/14)=(100/210)=(10/21). 10/21 is smaller than 16/33 so sheep B is more likely to survive.

To be reached by the wolf we need to remove 1 matchstick for each fence...

Case A : $P_A = \frac{8}{12}\cdot\frac{4}{11}+\frac{4}{12}\cdot\frac{8}{11} = 2\cdot(\frac{8}{12}\cdot\frac{4}{11}) = \frac{16}{33}$

Case B : $P_B = \frac{10}{15}\cdot\frac{5}{14}+\frac{5}{15}\cdot\frac{10}{14} = 2\cdot(\frac{10}{15}\cdot\frac{5}{10}) = \frac{10}{21}$

$P_A > P_B \Rightarrow B$ is most likely to survive

I'm not sure why, but I find this problem easier to think about when it is stated as the "Matching Socks Problem". It is a different context solved using the same method. Restate the problem as, "Drawer A has 8 white and 4 black socks, Drawer B has 10 white and 5 black socks. If I pull two socks at random from a drawer, will I be more likely to get a matching pair from Drawer A or Drawer B?" Pulling a matching pair of socks is equivalent to the sheep surviving. Some nice solutions strategies are at https://www.cut-the-knot.org/m/Probability/ProbabilityOfSocks.shtml

Clearly, the sheep in the figure with a larger number of matchsticks / number of segments is more likely to survive. B is a pair of pentagons and A is a pair of squares, Hence B is safer than A

The solution to this problem involves comparing the probabilities of survival in each case A (inner fence length 4) and B (inner fence length 5). The survival probability as a function of inner fence length will only increase or decrease with n, so this problem is equivalent to comparing n = 1 and n = 2. For n = 1, survival probability is 0, so B is the better chance.

Just saying, this problem can be done by simple logic. There are more sticks on the outside in case B and more sticks on the inside of case B compared to case A. Simple reasoning would conclude it's harder to get into the fence with more sticks.

No need for exact computation. P(death) = P(1 external AND 1 internal) = P(1 internal | 1 external) P(1 external). The probability to remove an external matchstick first is the same in both cases P(1 external) = 2n/(2n+n) = 2/3 (here n is the number of internal matchsticks). As P(1 external) is the same, we only need to compare probability to remove 1 internal matchstick after 1 external was removed, P(1 internal | 1 external) = n / (2n+n-1) = n/(3n-1)= 1/(3-1/n). When n is large, P(1 internal | 1 external) goes close to 1/3 (lower bound). However, with the decrease of n, the denominator decreases as well, so P(1 internal | 1 external) increases, and thus P(death) increases. Therefore, P(death) is higher for smaller n (case A). So B is more likely to survive.

The way I calculated probability is:

First find out in how many ways fatal combination can be choose. It would be number of matchsticks in outer fence multiplied by number of mathcsticks in inner fence. Then divide it by how many ways, 2 matchsticks can be chosen for each formation. For formation A, it is 12C2 and for formation B it is 15C2. So the probability is

A: $\frac{8*4}{12C2}$ B: $\frac{10*5}{15C2}$ /

Hence the probability for choosing fatal combination for B is less hence B is more safe.

I just went with the "more matches, more chances to survive" logic... the problem itself is pretty straightforward.

If two matchsticks are removed, there are three possible outcomes: (1) both will be removed from inner fence; (2) both will be removed from outer fence; or (3) one will be removed from each fence. The first two options will leave the sheep safe; the sheep will only be eaten if one matchstick is removed from each fence. Thus, the odds of survival will be 100% minus the odds of not surviving (or of one matchstick being removed from each fence).

The probability of Sheep A's survival is therefore 100% minus the probability of either (a) removing a matchstick from the outside fence followed by removing a matchstick from the inside fence or (b) removing a matchstick from the inside fence followed by removing a matchstick from the outside fence, as follows:

1-( $\frac{2}{3}$ * $\frac{4}{11}$ + $\frac{1}{3}$ * $\frac{8}{11}$ ) = 1- $\frac{16}{33}$ = $\frac{17}{33}$ = ~0.515

The probability of Sheep B's survival is, again, 100% minus the probability of either (a) removing a matchstick from the outside fence followed by removing a matchstick from the inside fence or (b) removing a matchstick from the inside fence followed by removing a matchstick from the outside fence, as follows:

1-( $\frac{2}{3}$ * $\frac{5}{14}$ + $\frac{1}{3}$ * $\frac{10}{14}$ ) = 1- $\frac{10}{21}$ = $\frac{11}{21}$ = ~0.524

So, Sheep B has a slightly better chance of survival.

For the sheep A the total number of different configurations of two removed matchsticks are ${12}\choose{2}$ = 66, whereas the configurations in which one matchstick from the outer fence AND one matchstick from the inner fence are missing are $8\times 4 = 32$ . Since all the removals are equiprobable then the probability of the sheep A be reached by the wolf is:

$P(A) = \frac{32}{66} = \frac{16}{33}$

For the sheep B we have ${15}\choose{2}$ = 105 total possible removals and $10\times 5 = 50$ fatal removals. Hence:

$P(B) = \frac{50}{105} = \frac{10}{21}$

Since $P(A) > P(B)$ then the sheep B is safer.

For a $n$ -side polygon, if the outer number of matchsticks is double than the inner one, we have ${3n}\choose{2}$ = $\frac{3n(3n - 1)}{2}$ and $2n^2$ fatal instances, so that:

$P = \frac{4n^2}{3n(3n - 1)} = \frac{4}{9 - 3/n}$

Hence, the larger $n$ is, the smaller $P$ becomes and the safer the sheep stays.

In the first situation, removing the first matchstick removes $12.5\%$ resp. $25\%$ of one of the fences. This greatly reduces the chance that the second matchstick will be taken from the same fence.

In the second situation, the percentages are only $10\%$ and $20\%$ . The chance that the second matchstick will come from the same fence decreases, but not as strongly is in the first situation.

Thus the sheep in the pentagonal setup is better protected.

Algebraic generalization

If the inner fence has $m$ and the outer fence $n$ sections, the probability of the wolf getting the sheep is $\mathbf P = \frac{mn}{\binom{n+m}{2}} = \frac{2mn}{(m+n)(m+n-1)}.$ When comparing two situations where the inner fence makes up fraction $\alpha$ of the total, so that $m = \alpha N, n = (1-alpha)N$ , we have $\mathbf P = \alpha(1-\alpha)\left(1 + \frac{1}{N-1}\right).$ Clearly, a greater value of $N$ results in a smaller chance that the wolf gets the sheep.

P(A survives) = P(we remove 2 matches from outer boundary) + P(we remove two matches from inner boundary) = 2 $\frac{8*7}{(\frac{16}{2})}= 0.933333,,,,,,$ .

P(B survives) = 2 $\frac{10*9}{(\frac{20}{2})} = 0.94736-----$ . So B survives.

For Sheep A to survive, we must remove two matchsticks exclusively from either the eight outer fence pieces OR from the four inner fence pieces, which has probability:

$P(A) = \frac{C^{8}_{2} + C^{4}_{2}}{C^{12}_{2}} = \frac{17}{33} \approx \boxed{0.5151}.$

Using the same reasoning for Sheep B (ten outer pieces & five inner pieces) we obtain the probability:

$P(B) = \frac{C^{10}_{2} + C^{5}_{2}}{C^{15}_{2}} = \frac{11}{21} \approx \boxed{0.5283}.$

Hence, Sheep B has the greater chance for survival $(P(B) > P(A))$ . NOTE: $C^{x}_{y} = \frac{x!}{y! (x-y)!}.$