96 of 100: Murphy's Probability
Three people all set down their identical notebooks on a table. On the way out, they each randomly pick up one of the notebooks. What is the probability that none of the three people pick up the notebook that they started with?
A chart or table may help sort through the possibilities in this scenario.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
The math is correct but the explanation is unclear. Suppose person A selects notebook B. Then person B can select either of the remaining notebooks, but if he chooses notebook A then person C will end up with his own notebook. In fact, once person A chooses a notebook that is not his own (2 choices), there is exactly one distribution of the remaining notebooks that results in no notebook being chosen by its owner (not "no more than 1"). Note that the analysis is more complex when n > 3, because the number of derangements is most naturally defined recursively.
Log in to reply
@Kazem Sepehrinia none of the three people pick up their own notebook is 2 ways why we use 2x1 ways.
Log in to reply
First person has 2 ways to not pick her/his own notebook. Second has one way. Its 2x1.
Log in to reply
@Kazem Sepehrinia – @Bala Chandar @Lynn Kiaer
The possible combinations are {(1,2,3), (1,3,2), (2,3,1), (2,1,3), (3,1,2), (3,2,1)} and the number of possibilities of first person not taking “1” is 4 ways. It is not 2 ways if you consider all the combinations.
The remaining combinations are {(2,3,1), (2,1,3), (3,1,2), (3,2,1)} and now the number of possibilities of the second person not taking “2” is 3 ways. It is not 1 way if you consider all the combinations.
The remaining combinations are {(2,3,1), (2,1,3), (3,1,2)} and now the number of possibilities of the third person not taking “3” is 2 ways.
For three combinations, none of the three people pick up their own notebook is 2 ways with the following combinations{(2,3,1),(3,1,2)}. It is not 2x1 ways.
If we go with the order First person, Second person and third person not selecting their own notebook, then the last person’s possibilities are the total derangement(!3=2).
Similarly, for 4 notebooks we will get for first person 18 ways, and second person 14 ways, third person 11 ways and fourth person we will get 9 ways.(!4=9) For four combinations none of the four people pick up their own notebook is 9 ways.
Why the solution not considering all combinations and limiting the combinations. Because of the limitations It only works for the given problem (n<4) and the solution is not generic.
Log in to reply
@Venkatachalam J – The answer was edited to remove the misleading language after I made my comment. The answer was always correct. Now it is a correct answer with no explanation (or a misleading one, as a naive reader might try to generalize from it, and a good solution should make clear that this solution is not generalizable). That point is made clear in the comments of others.
Log in to reply
@Lynn Kiaer – Let say first person can take notebook-2 or notebook-3. (has 2 choices)
First person taking notebook-2(case-1) and First person taking notebook-3(case-2).
The second person can take notebook-1 or notebook-3.
Consider case-1 then the possible combinations are (2,1, _) or (2,3, _)
Consider case-2 then the possible combinations are (3,1, _) or (3,3, _) . We know that (3,3, _) is not possible so there are 3 choices for the second person to choose his choice.
The third person can take notebook-2 or notebook-3 consider the previous results (2,1, _) or (2,3, _) or (3,1, _) the possible combinations are {(2,3,1),(3,1,2)}. Now we get the final result none of the three people pick up their own notebook is 2 ways.
While choosing the first persons choice, with out considering second and third person choice we get 2 choices. (2, _ , _) or (3 , _, _). In the same way if we did not consider the third persons choice we will get 3 choices (2,1, _) or (2,3, _) or (3,1, _) for the second person. Now considering the first and second person with checking the condition of the third person we will get two choices (2,3,1),(3,1,2). If we considering all the three person we got 2 ways.
@Kazem Sepehrinia For n=3, none of the three people pick up their own notebook is 2. (The answer posted as In 2 × 1 ways, none of the three people pick up their own notebook). It looks like there are 3! ways of picking up notebooks, In (3-1)! ways, none of the three people pick up their own notebook.
In the same way we will not solve for higher order. For example if n=4, none of the four people pick up their own notebook. How to express it as posted for n=3.(2×1 ways)? 3×2×1 ways will not give correct solution. Need to update the representation 2 × 1 ways.
For n=3, none of the three people pick up their own notebook =3! ∑ r = 0 3 ( − 1 ) r ( r ! 1 ) =3!( 0 ! 0 - 1 ! 1 + 2 ! 1 - 3 ! 1 )=6(1-1+ 2 1 - 6 1 )=6( 6 2 ) = 2 and
For n=4, none of the four people pick up their own notebook =4! ∑ r = 0 4 ( − 1 ) r ( r ! 1 ) =4! ∑ r = 0 4 ( − 1 ) r ( r ! 1 ) =4!( 0 ! 0 - 1 ! 1 + 2 ! 1 - 3 ! 1 + 4 ! 1 )=8
In general, none of the 'n' people pick up their own notebook=n!( ∑ r = 0 n ( − 1 ) r ( r ! 1 )
Log in to reply
My solution works fine for three people. I have no claim about extending it to more people. Thanks for the point.
Relevant wiki: Derangements
By exploring all possibilities we will get the following solution:
(or)
In General, for 'n' people and 'n' notebook, the probability that none of the 'n' people pick up the notebook that they started with= (
n
!
!
n
)
Formula:
For 'n' people and 'n' notebook, the probability that none of the 'n' people pick up the notebook that they started with=
n
!
!
n
=
n
!
n
!
∑
r
=
0
n
(
−
1
)
r
(
r
!
1
)
=
∑
r
=
0
n
(
−
1
)
r
(
r
!
1
)
Beautifully aranged - I love answers like these, a they are so clear & I can use them with young students. Thank you
Looked again - doesn't detract from what I said - it still works beautifully - but what is !3 - I haven't seen this notation before, and had no joy when trying to look it up
Log in to reply
Click the relevant wiki link derangements "https://brilliant.org/wiki/derangements/" (or) click "http://mathworld.wolfram.com/Derangement.html". You will get the details.
Log in to reply
thanks - i have learnt something - I did go onto Wolfram, but I put !3 and then 'factorial' into the search box
Let's say person A starts with notebook 1, person B with notebook 2 and person C with notebook 3. When picking up their notebooks randomly there are six possible situations.
| person A get notebook 1 | person B get notebook 2 | person C get notebook 3 | ⇒ | all three persons pick their own notebook |
| person A get notebook 1 | person B get notebook 3 | person C get notebook 2 | ⇒ | person A pick their own notebook |
| person A get notebook 2 | person B get notebook 1 | person C get notebook 3 | ⇒ | person C pick their own notebook |
| person A get notebook 2 | person B get notebook 3 | person C get notebook 1 | ⇒ | none pick their own notebook |
| person A get notebook 3 | person B get notebook 1 | person C get notebook 2 | ⇒ | none pick their own notebook |
| person A get notebook 3 | person B get notebook 2 | person C get notebook 1 | ⇒ | person B pick their own notebook |
So the probability that none of the three people pick up their own notebook is 6 2 = 3 1 .
A bit awkward, but quick and painless solution: one of the people pick up a notebook, it has a 2/3 chance that it's not theirs. One of the other people then have a 1/2 chance to not pick up his own (the other one doesn't matter, since the first person picked his). So (2/3)/2=1/3.
Slight issue here - the problem did not say they were all male. This does matter if you teach mixed-gender groups. Sorry to be pedantic, especially if you're EAL - but 'their' is a gender neutral pronoun
Log in to reply
Edited. Not that I care too much :p
Log in to reply
I can't just post you smiley face - the website won't let me - but cheers for that. Liked the solution, though
The probability for every person picking wrong book is 3 2
and there are 2 ways that none of them pick up the initial 1 they started with
so, the probability is= 3 2 × 2 1 = ( 3 1 )
Don't you mean that the probability of ANY person picking up the wrong book is 2/3? The end result is that the probability of EVERY person picking up the wrong book is 1/3.
Log in to reply
I agree with Robert. Also, why do you downvote every constructively critical comment you get instead of acting on it and discussing it with your fellow Brilliant users?
Log in to reply
actually, i thought the argument was irrelevant.and i never get back from any constructively critical comment.i always try to reply and make an logical argument with others.you can see it from my last solutions.if any mathematical problems & critics come ,then let me know,please.i am always eager to learn and share.
P(none of them pick their correct note books) = P(1st does not pick his own)P(2nd does not pick his own notebook) = 3 2 × 2 1 = 3 1 .
There are 2 ways of distributing the notebooks so that no one has the correct notebook.
If we denote " A picking up B's notebook by A-> B, we will notice that one cannot realize the above scenario of no one picking up the correct notebook if we have a cycle involving only 2 people . For e.g, if A -> B and B-> A , then C-> C which is not the desired scenario.
So the scenarios are :
1). A-> B and B-> C and C-> A
2) .A-> C and C-> B and B-> A.
So there are 2 possible ways in which no one picks up the correct notebook.
There are 3! = 6 ways of distributing the notebooks among A, B and C.
So , the desired probability = 2/6 = 1/3
According to derrangement rule
Total no of derrangement of 3 units is 2
We know total case is 3!=6
Then probability = 1/3
I thought of three things that could happen. It is impossible for one person to get the wrong notebook and the two others to get the right notebook. So, ether one person gets the right notebook and the other two to get the wrong one, they all get the right one, or they all get the wrong one. So one of these three examples is the one that they are asking for. One of three is the same as 3 1 .
Man 1 can select others book by 2/3and after this the two book left. So man 2 can select other book by1/2 so finally probability of getting dearranged scenario is 2/3*1/2=1/3
Imagine person 1 picked up the notebook on the left, person 2 picked up the notebook in the middle and person 3 picked up the notebook on the right.
Imagine each notebook has the number "1", "2", or "3" on it identifying which person owns which notebook.
The question becomes: What are the permutations of the ordered triple (1,2,3) which leaves each number in a different position than the one corresponding to its name (position 1 is the leftmost digit, position 2 is the middle digit, position 3 is the right digit. So (1,2,3) has all the digits in their named positions.
Here is a picture can you can use to solve this problem.
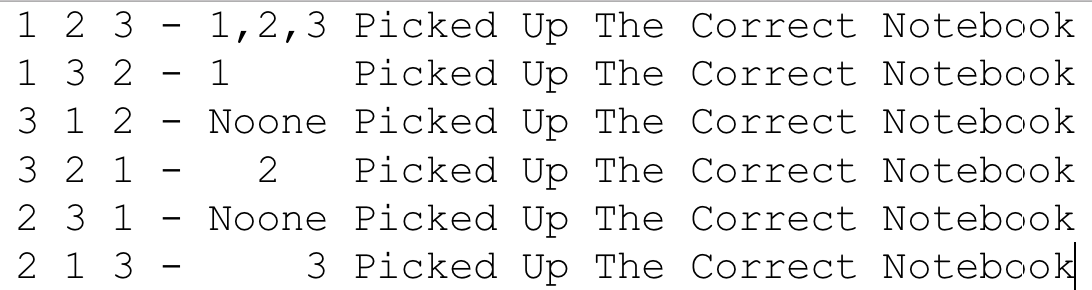
The really simple solution is just that there are 3 notebooks and you need to pick of the 3! 1/3
The probability of first person picking wrong book is 2/3
In each 1/3 probability branch the probability of picking wrong books by each of remaining two persons is 1/2
There are 3 × 2 × 1 = 6 ways of picking up notebooks. In 2 × 1 ways, none of the three people pick up their own notebook. Thus the probability is 6 2 = 3 1 .