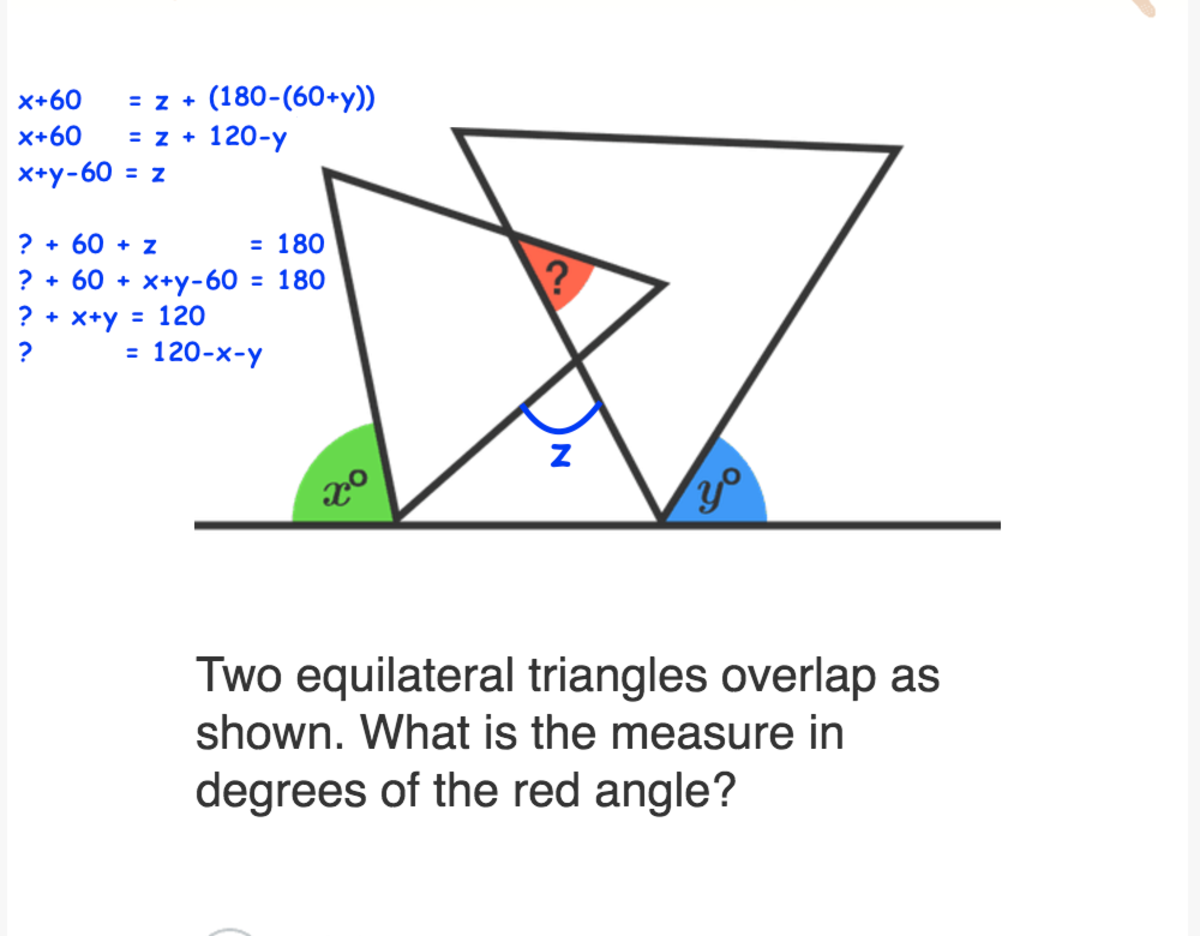
98 of 100: Triangle Tangle

Let ?= ${\color{#D61F06}z}$ . Angles of yellow triangle are $180-x$ (left base), $120-y$ (right base), and $60-{\color{#D61F06}z}$ (top angle). Sum of angles gives $180-x+120-y+60-{\color{#D61F06}z}=180$ and $\boxed{{\color{#D61F06}z}=180-x-y}.$

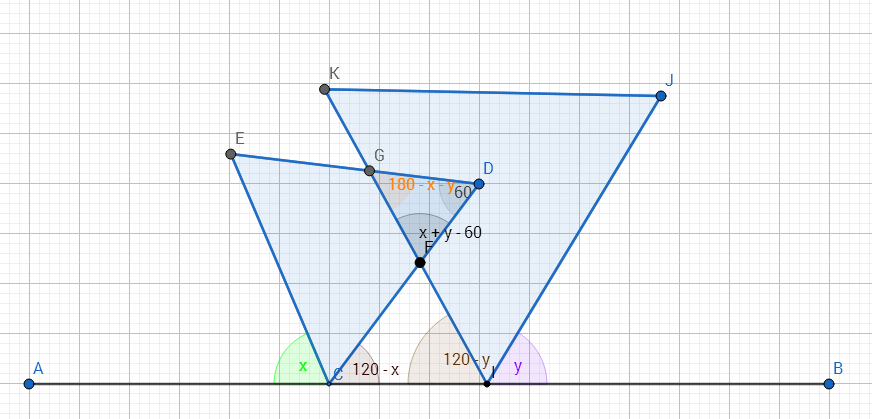
$Step ~ 1$ ACB is a straight line. So,

$\angle ACE +\angle ECD +\angle DCB = 180^\circ$

$\implies x^\circ + 60^\circ +\angle DCB =180^\circ$

$\implies \angle DCB = 120^\circ - x^\circ$

Similarly,

$\angle KIA = 120^\circ - y^\circ$

$Step ~ 2$ In triangle CFI,

$\angle ICF +\angle CIF +\angle CFI = 180^\circ$

$\implies 120^\circ - x^\circ + 120^\circ - y^\circ +\angle CFI = 180^\circ$

$\implies \angle CFI = x^\circ +y^\circ - 60^\circ$

$Step ~ 3$

$\angle GFD = \angle CFI = x^\circ +y^\circ - 60^\circ$

Now, from triangle GFD,

$\angle GFD + \angle GDF +\angle FGD = 180^\circ$

$\implies x^\circ +y^\circ -60^\circ +60^\circ +\angle FGD = 180^\circ$

$\implies \angle FGD = 180^\circ - x^\circ -y^\circ$

Common sense here works great. It is obvious we can change the angles as we wish, and still end up with a working solution. The size wasn't given, so therefore it must also be irrelevant. Therefore, we look at the solutions, and see that $180 - x - y$ is the only solution with equal coefficients of x and y.

Therefore, $180 - x - y$ is the solution.

An algebraic solution: Call the unknown angle $z$ (in degrees). It is clear that $z$ depends linearly on $x$ and $y$ . That is, $z = ax + by +c$ . Furthermore, there are three situations in which the answer is clear: $\begin{array}{llcl}x=60 & y=60 & \to & z=60\\ x=120 & y=60 & \to & z=0\\ x=120 & y=0 & \to & z=60\end{array}$ Three equations with three unknowns ( $a, b, c$ ), readily yield the solution $a, b, c = -1, -1, 180$ Thus, $z=\fbox{\$180 - x - y\$}$ .

If base of smaller triangle is extended so as to meet ground, a triangle gets formed with following three angles;.
1. Red angle at top vertex.
2. Base angle (60 + y).
3. Base angle (x - 60).
Sum of the angles being 180°, the Red angle works out to (180 - x - y).

Here is a quick solution: There are no restrictions on the values of x or y. Therefore the solution must work for the values x=60 degrees and y=60 degrees. This case is easy to solve. The missing red angle must be 60 degrees. The only choice that yields 60 is 180-x-y.

Notice: In the small triangle one angle is 60 and one angle is a vertical angle with a triangle that has as its sidex parts of the equilateral triangles. So, call that vertical angle z.

Notice: x+60 is an exterior angle and is equal to the sum of z an 180-(60+y)

Check out the image below for the rest of the solution.

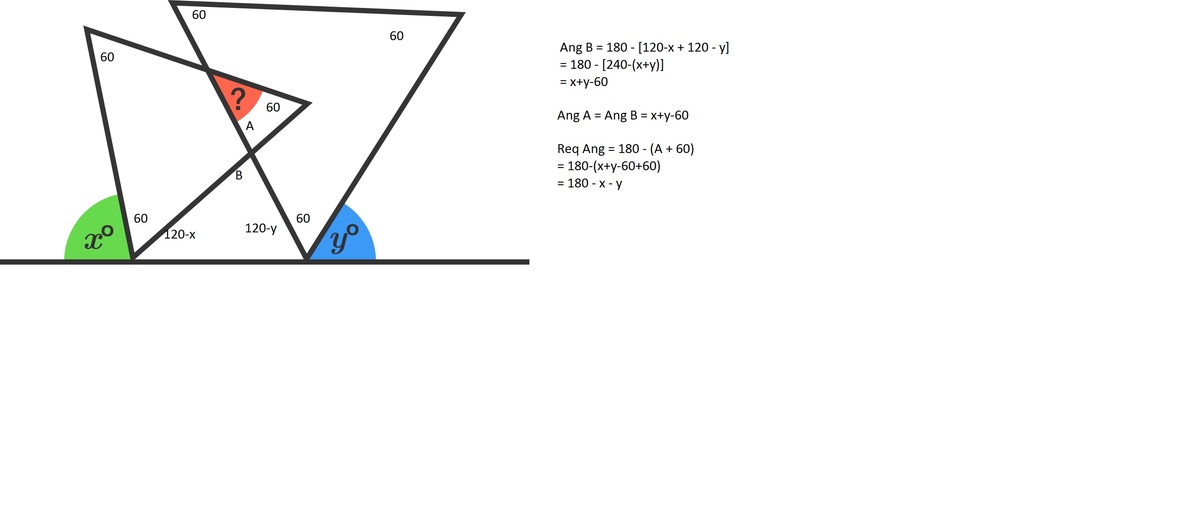
In the smaller triangle between the two equilateral triangles, the base

angles are 120 – x, and 120 – y degrees. So the third angle of this triangle

is 180 – [(120 – x) + (120 – y)] = x + y – 60 degrees. So, the measure of the

angle in red z is:

z = 180 – [60 + (x + y – 60)] = 180 – (x + y ) degrees.

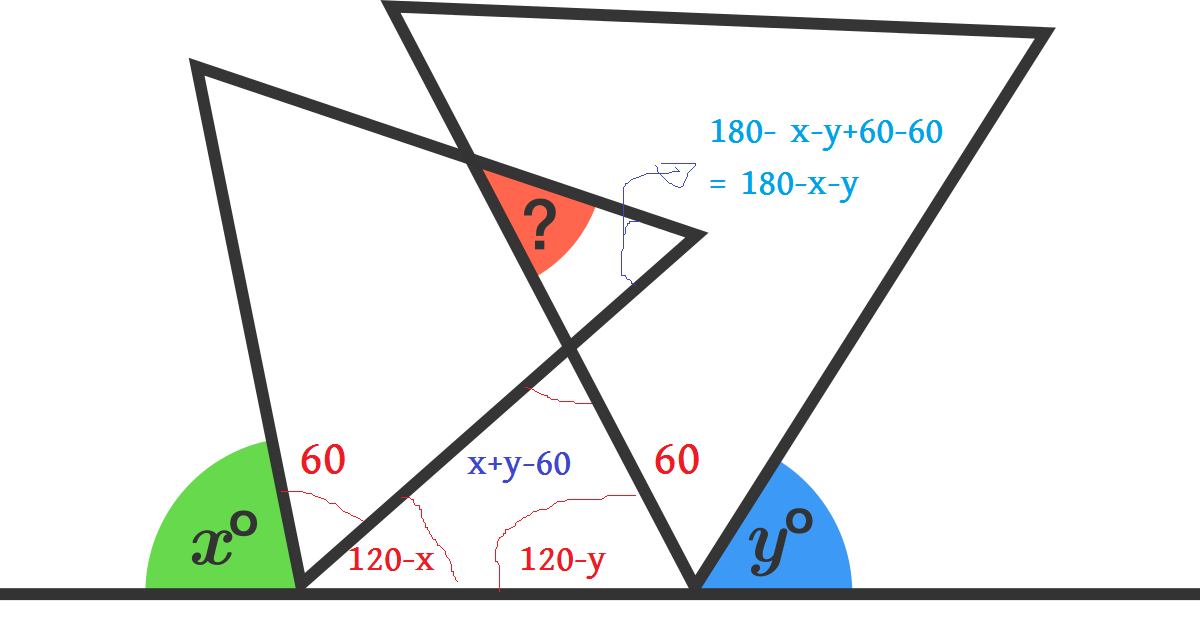
On the "floor", there are two trios of angles that add up to 180 degrees. In one, they are an angle in one of the equilateral triangles and angle x, which means that their measures are 60 and x, which means that the other is 180-(60+x), or 120-x. In the other trio, the third angle is 120-y. These two angles form a triangle whose third angle is 180-[(120-x)+(120-y)], or 180-(240-x-y), or x+y-60. The final triangle has three angles: The mystery angle, an angle in the first triangle, and an angle vertical to the angle we just calculated. This means that their angle measures are 60, x+y-60, and an unknown value. The mystery angle is 180-(60+x+y-60), or 180-(x+y) or 180-x-y).

I "solved" this without calculating any angles or solving any equations. I just noted that if you tilt the left triangle to the left, Angle "x" decreases while Angle "?" increases. This inverse relationship told me that the sign on the x coefficient had to be negative (which eliminated the second answer choice). Then I imagined tilting the right triangle to the left and noted that this increased Angle "y" while decreasing Angle "?". Again, that says the sign on the y coefficient is negative (which eliminated the first and third answer choices). With the second, first, and third choices eliminated, only the fourth answer choice, "180 - x - y" remained. Easy. And no calculations necessary!

easy one.primary level.

Let direction 0 degrees be horizontal to the right and positive directions counter clockwise.

Then the upper leg of the red angle has direction

180 - x - 120 = 60 - x

and the lower leg has direction

y + 60 - 180 = y - 120

The red angle is upper leg direction minus lower leg direction

60 - x - y + 120 = 180 - x - y