99 of 100: Penultimate Puzzle
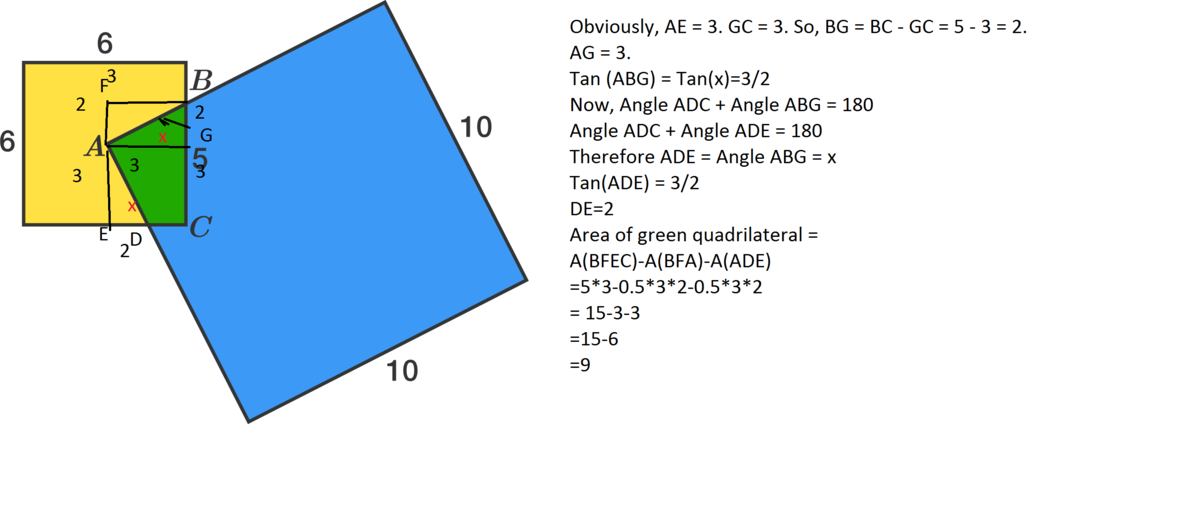
A square of side length 10 is placed so that its corner, A , is exactly at the center of a square of side length 6. The squares intersect at point B as shown; the length of line segment B C (connecting B to a corner of the smaller square) is 5.
What is the area of the green quadrilateral?
If you get stuck, try drawing some lines on the figure to help you out.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
17 solutions
That's what I did, but it was more a guess than anything - how do you know that the 2 triangles are congruent? (Then I can pretend my solution came totally through great maths, and wasn't a guess at all :) )
Log in to reply
I did this problem before.
Log in to reply
Meh - I don't think that counts :)
Log in to reply
@Katherine Barker – Both of the smaller angles at A are congruent since they are both complementary to the larger angle at A.
Log in to reply
@Judy Wheeler – Oh yes - I see it now. Thanks
The angles at A of the two right triangles are equal. See how the two hypotenuses form a right angle, and the two adjacent sides do too. And the length of the adjacent sides are both 3, obviously. So the triangles are congruent.
Log in to reply
Sorry - I think I'm being dense - but why are the 2 angles at A equal? Thanks to those helping me out with this.
Solved it the same way.
Shifting pieces is the definitely the best way to solve this problem.
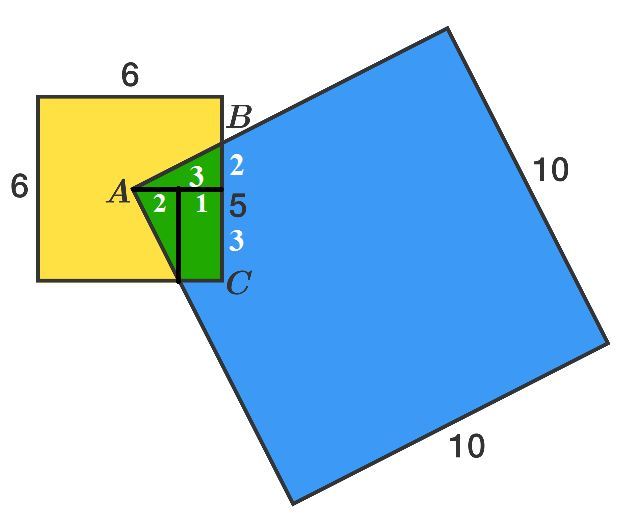
Since A is in the center of the yellow square, and the intersecting blue is also square, the green area will always be 1/4 of the area of yellow, no matter how blue is rotated. yellow = 6 x 6 = 36. Green = 1/4 x 36 = 9
Log in to reply
I can sort of see that - and that's how the 2 people below solved this - but I'm really keen to get to the bottom of the 'congruent triangles' solution, as that's what I first thought of, even though I couldn't actually prove it.
That's how I solved it as well.
Yes. It's right. I don't know even why there is 5.)
beautifully done! :)
Simple and elegant.
This is the visual representation of my intuition; had the larger square intersected two corners of the smaller, or evenly bisected two edges, the overlapping area was in both cases 1/4 of the smaller. Extending it to four larger squares, to demonstrate an arbitrary angle, was the proof that eluded me.
Cheers!
Can't understand -how did u get the area is 1/4th of the small square?
Log in to reply
Hey Shubhajit! I drew in tree exact copies of the blue square to form a larger square centered exactly in the middle of the yellow square. As you can see, now the yellow square is divided evenly into four. Given that the total yellow area is 36, the overlapping green area must be 9.
Let's extend the two sides of the big square through A. Then we get a cross with A in the middle that cuts the small square into 4 congruent pieces (rotated by multiples of 90° around A), one of them being the green one. The area is then a quarter of the small square, so 9.
Excellent solution - really clearly presented.
The location of point B is quite irrelevant. Extending the sides of the blue square shows that the yellow square is divided into four congruent part, each with area
4
6
2
=
9
.
The green area is made up of two right triangles, DBC and ABD.
We know the base and height of DBC, so its area is 2 5 \ .
The line BD, the shared hyponenteuse, is sqrt(26). As ABD is a right isosceles triangle, we know AB=AD= sqrt (13).
Area of ABD is 2 1 3 , So the entire green area is 2 5 + 2 1 3 = 2 1 8 = 9.
Possibly stupid question. How can you guarantee that the length of DC is 1?
Log in to reply
Because the angle at A is right, we know the sides of the blue square pivot evenly across the lines of the yellow square.
and that ADB is a right isoceles triangle? It doesn't have to be, I wouldn't think, by any definition.
Log in to reply
AD = AB because they both hit the side of the square at the same point 1 along from the vertices.
Yes, but what's the proof that both "hit the side of the square at the same point 1 along the vertices?" Just trying to make sure I'm tracking....
Simply rotate the blue square so the sides pass through the corners of the yellow square. Then it's clear that the green section is 1/4 of the yellow square = (6*6)/4 = 9
Bisect the yellow square. The divides the quadrilateral into a trapezoid and a right triangle. Since the point is at the center of the square, the legs of the triangle are 3 and 2. Also, the angle on this line is complementary to the other angle in the triangle and the adjacent angle in the trapezoid. This means that the angles are congruent, so the trapezoid is part of a similar triangle, where one of the side lengths is 3. The other leg, by proportions, is 4.5. The side of the trapezoid is 3 units down, which is 1/3 of the way upwards, so its length is 1/3 of 3, which is 1. This means that the bases of the trapezoid are 1 and 3, and the height is 3. The sum of the areas of the triangle and the trapezoid are therefore 2•3/2+3(1+3)/2, or 3+3•4/2 or 3+3•2 or 3+6 or 9.
ABG is not 45 degree. It would be 45 degree if B was the vertix of the small square. That's why your approach is faulty from the beginning, and results in a figure that is not one of the choices.
Log in to reply
Yes, you are right. I wonder how i could have made such a glaring mistake. Thanks for pointing it out. Obviously,the length of the segment from A to the segment of the square is 3 and not 2. The corresponding angles are not FBA and ABG but FBA and BAG. Apologies once again !!
Apologies, i do not know how i could have made such a glaring mistake. Obviously, AE = 3 and not 2. Submitting the edited solution
For any two similar squares attached in the same way, such that the side length of the larger square is greater than AC, and given any angle of rotation, the quadrilateral formed will have an area one quarter the area of the smaller square.
If you imagine rotating the blue triangle from point A, you get a green square with side length 3, and if you solve for that area, you get 9.
Let's label the fourth point of the quadrilateral D. The area of A B C D = A B C + A C D = 2 5 ⋅ 3 + 2 3 ⋅ ∣ C D ∣ = 2 3 ( 5 + ∣ C D ∣ ) . And because the answer is an integer, ∣ C D + 5 ∣ must be divisible by two. This means that ∣ C D ∣ is 1, 3 or 5 because otherwise it would go beyond bounds. A good guess that it's the smallest of the three, so the answer is 2 3 ( 5 + 1 ) = 9
xD
green region has two triangles. the smaller one is equal with the triangle in yellow region under the digonal and above the side of the bigger aquare.
=> similar triangles with two angles and the side in between equal as the half of the diagonal of the small square.
this results in base of 1 with height 3 => 1st triangle inside the green region. the other triangle is a simple triangle with height 3 and base 5.
area: 9
 Slope of AB= 2/3, So that of AB= 3/2. Area= upper triangle+ lower rectangle + lower triangle = 1/2
3
2+ 3
1+ 1/2
2*3 = 3+3+3 =9
Slope of AB= 2/3, So that of AB= 3/2. Area= upper triangle+ lower rectangle + lower triangle = 1/2
3
2+ 3
1+ 1/2
2*3 = 3+3+3 =9
If you consider the rotation of the blue square about point A, there are two configurations that would obviously make the green are 1/4 of the smaller square- 9, the point when the sides are perpendicular and the point when the the blue squares sides intersect the vertices. Noticing this leads us to consider if the area changes for any rotation, and drawing in a horizontal and vertical line through point A, it is simple to consider that for any rotation the small yellow triangle will be congruent to the small green triangle. Thus any rotation covers 1/4 of the smaller square- 9 (also true for any blue square with sides longer than half the yellow's diagonal).
To throw some coordinate geometry at the problem: if we center the plane at A = ( 0 , 0 ) , such that the smaller square has horizontal and vertical sides, then B = ( 3 , 2 ) and C = ( 3 , − 3 ) . Let D be the fourth corner of the green quadrilateral. Then since A D ⊥ A B , the slopes of these two lines are negative reciprocals. Thus D = ( 2 , − 3 ) . Now we have enough information to determine the area of the quadrilateral: A r e a ( □ A B C D ) = A r e a ( △ A B C ) + A r e a ( △ A B D ) = 0 . 5 ∗ 3 ∗ 5 + 0 . 5 ∗ 3 ∗ 1 = 9
This generalizes: if B = ( 3 , x ) then D = ( x , − 3 ) then the area of the quadrilateral is A r e a ( □ A B C D ) = A r e a ( △ A B C ) + A r e a ( △ A B D ) = 0 . 5 ∗ 3 ∗ ( 3 + x ) + 0 . 5 ∗ 3 ∗ ( 3 − x ) = 9
Set the coordinate axes such that the coordinates of the square (-3. -3),
C (3, -3), (3, 3), and (-3, 3). Therefore the center of this square lies at (0, 0).
Then A (0, 0) and B (3, 2). The slope of AB is:
m = 3 2 .
The slope of the side of the largest square is m’ = - 2 3 and theequation of this side that passes through A is y = - 2 3 x. So if we
set y = -3, then x = 2. Therefore the the side of the largest square intersectsthe smallest square at D (2, -3). Then, by distance formula:
AB = 1 3 , AD = 1 3 , and CD = 1
Then the area of polygon ABCD = ½[ AB\times AD + BC \times CD] = ½(13 + 5) = 9.
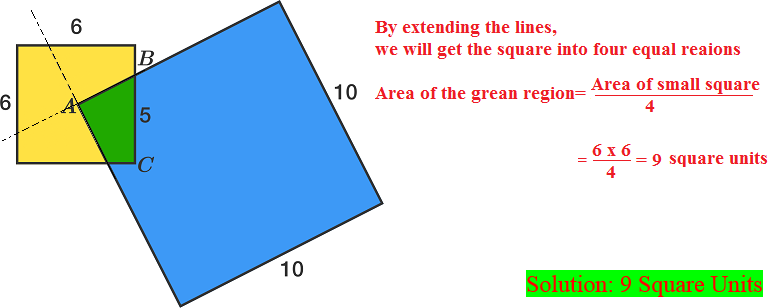
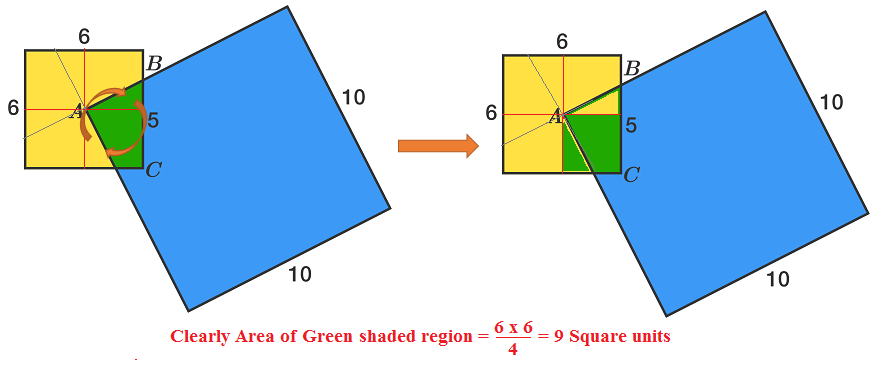
3 x 3 = 9