Dedication pays off!

Algebra Level 5

$\huge x^{x^{x+3}} \times x^{2x^{x+2}} = a^{a^{(1-a)/a}}$

For all $x$ and $a$ real numbers that satisfy the equation above, and given that

$\Large x^{-x} \times \left( \frac1a\right)^{-\frac1a}$

can be expressed as $\displaystyle x^b$ , where $b$ is an integer, find the value of $b$ .

The answer is 2.

3 solutions

Gabriel Benício
Nov 16, 2015

First we have: $\displaystyle (x^{x^{x+3}})(x^{2x^{x+2}})=x^{x^{x}x^{2}(x+2)}=x^{x^{x+2}(x+2)}=(x^{x+2})^{x^{x+2}}$ .

On the other side: $a^{a^{\frac{1-a}{a}}} =a^{a^{\frac{1}{a}-1}}=a^{a^{-1}a^{\frac{1}{a}}}=(a^{\frac{1}{a}})^{a^{\frac{1}{a}}}$

Let $m=x^{x+2}$ and $n=a^({\frac{1}{a})}=(\frac{1}{a})^{-(\frac{1}{a})}$ , then, from the first equation, we have

$m^m=n^n \Longrightarrow m=n$

Finally, we have

$x^{x+2}=(\frac{1}{a})^{-(\frac{1}{a})} \Longrightarrow x^2=x^{-x}(\frac{1}{a})^{-(\frac{1}{a})}$

Then, $b=2$

Since x = $-1 \pm \sqrt2$ as constants finally which are not arbitrary for an identity,

$- x + \frac{1}{x}$ = 2 is not the only thing because case of base x = a = 1 was ignored.

With x = a = 1 substituted into original equation,

L.H.S. = 1 = R.H.S.

$b = - 1 + \frac{1}{1}$ = 0 else $1^{?}$ = $1^b$ ,

b = 0, 1, 2 and etc with base 1 of original equation to take effect!

The answer of this question becomes ambiguous.

Only when I try to read the mind of the author, I got 2 as the answer wanted.

Lu Chee Ket - 5 years, 6 months ago

I updated the problem to specify that $b$ must be a integer satisfying the equation for all $x$ and $a$ that satisfy the original equation. Thanks. :)

Gabriel Benício - 5 years, 6 months ago

b = 0, 1 and 2 were integers. The thing is you ought to say that x (and also a) is (are) not an integer (example: 1).

Lu Chee Ket - 5 years, 6 months ago

Damn I solved it them by mistake clicked discuss solution

Shreyash Rai - 5 years, 6 months ago

Mark Hennings
Nov 19, 2015

If we drop the (unstated) requirement that $b$ be an integer, there is yet another solution. We have $\big(x^{x+2}\big)^{x^{x+2}} \; =\; a^{a^{\frac{1-a}{a}}}$ and this second term is equal to $a^a$ when $a=\tfrac12$ . Thus we can have $a=\tfrac12$ and $x^{x+2} = a = \tfrac12$ , which gives an approximate numerical solution $x = 0.779269$ . The function $x \mapsto x^{x+2}$ is strictly increasing on $[0,\infty)$ , and so the equation $x^{x+2} = \tfrac12$ has a unique solution.

Then $(a^{-1})^{-a^{-1}} \,=\, a^{a^{-1}} \,=\, \tfrac14 \,=\, a^2 \,=\, x^{2x+4}$ , so that $x^b = x^{-x+2x+4} \,=\, x^{x+4}$ , and hence $b = x+4 = 4.779269$ .

Mark,

Why / how are you assuming the value of 'a' to be equal to 1/2 ?

Raghunandana Ravindra - 5 years, 6 months ago

Because I want (1-a)/a to be 1.

Mark Hennings - 5 years, 6 months ago

But that value of $b$ don't stand for all $a$ and $x$ in that expression.

Gabriel Benício - 5 years, 6 months ago

@Gabriel Benício – The real problem is that you state that $m^m = n^n$ implies that $m=n$ . It does not. The function $y = x^x$ has a turning point at $x = e^{-1}$ , being decreasing for $0 < x < e^{-1}$ and increasing for $x > e^{-1}$ .

If you could easily guarantee that $x^{x+2}$ and $a^{\frac{1}{a}}$ are both greater than $e^{-1}$ , then you would be able to deduce that $x^{x+2} = a^{\frac{1}{a}}$ , which is what you want. That would be messy!

The simplest way of removing all difficulty would simply be to restrict solutions of the first identity to the range $x,a \ge 1$ . In that case $x^{x+2}$ and $a^{\frac{1}{a}}$ are both at least $1$ , and so you can deduce that $x^{x+2} = a^{\frac{1}{a}}$ , and your proof will work.

Mark Hennings - 5 years, 6 months ago

@Gabriel Benício – But then your solution $b=2$ does not work for my values of $x$ and $a$ , which do satisfy the first equation. In that sense, your answer is as wrong as mine!

Mark Hennings - 5 years, 6 months ago

Lu Chee Ket
Nov 18, 2015

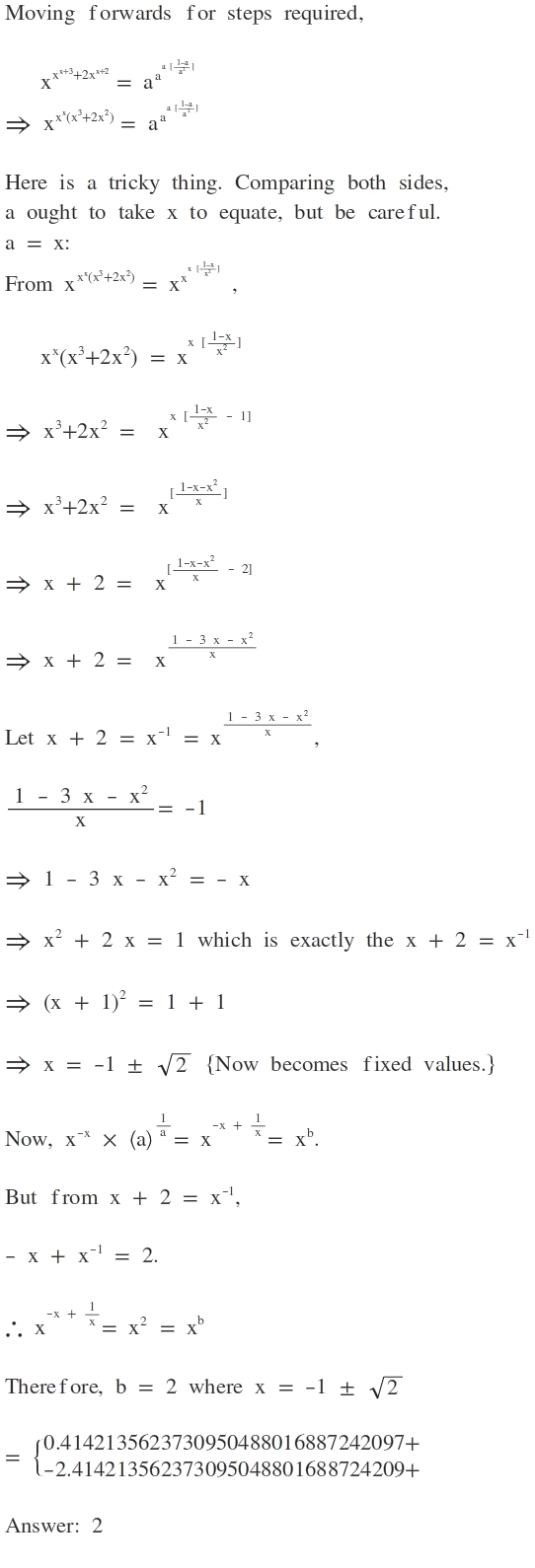
The system of Brilliant could have made this page looked small to you. Please drag for another tag at the top to view with enlargement allowed. b = 0, 1, 2 and etc if not guessing the mind of the author when base 1 of original equation is considered.

Dedication pays off!

The answer is 2.

3 solutions

0 pending reports