Deep impact

Relevant wiki: Lagrangian Mechanics

The velocity $v$ of the moon is composed of a radial velocity $\dot r$ and a tangential velocity $r \dot \phi$ whose vectors are perpendicular to each other. Therefore, the total energy can be converted to $E = \frac{1}{2} m v^2 + V(r) = \frac{1}{2} m \dot r^2 + \frac{1}{2} m r^2 \dot \phi^2 + V(r) = \frac{1}{2} m \dot r^2 + \frac{L^2}{2 m r^2} + V(r) = \frac{1}{2} m \dot r^2 + V_\text{eff}(r)$ with the angular momentum $L$ and the effective potential $V_\text{eff}(r) = \frac{L^2}{2 m r^2} - G \frac{M m}{r}$ which contains the kinetic energy of the angular motion. This representation has the advantage, that the energy depends only on the radius $r$ and its velocity $\dot r$ , so that we describe a motion in one dimension. The function $V_\text{eff} (r)$ takes the following form: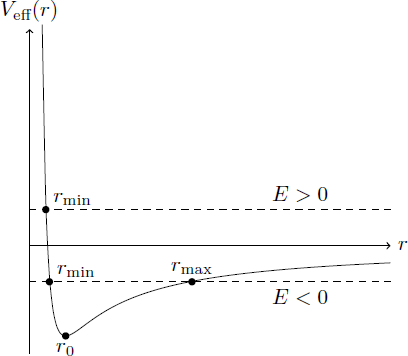 For a given energy $E$ , the radial distance $r$ can only assume values ​​with $V_\text{eff}(r) \leq E$ . Therefore, we can distinguish two cases:

• $E < 0$ : The radial distance is bounded by a minimal radius $r_\text{min}$ and maximal radius $r_\text{max}$ , so that $r_\text{min} \leq r \leq r_\text{max}$ . The orbit is a closed elliptical orbit. For the special case $r_\text{max} = r_\text{min} = r_0$ (minimum of $V_\text{eff}(r)$ , the orbit has a perfect circular shape.

• $E \geq 0$ : There is no maximum radius $r_\text{max}$ , so that the radial distance $r$ can take abitrary large values. The orbits are open, so that the moon orbits the earth only once, then continually moves away from it and never returns.

Before the impact, the moon has a circular orbit with radius $r_0$ , so that effective potential is minimal $V_\text{eff}'(r_0) = - \frac{L^2}{m r_0^3} + G \frac{M m}{r_0^2} \stackrel{!}{=} 0 \quad \Rightarrow \quad r_0 = \frac{L^2}{G M m^2}$ After the impact, the moon's potential takes the value $V_\text{eff}(r_0) = \frac{L^2}{m r_0^2} + G \frac{(M/2) m}{r_0} = 0$ This fulfills the condition for an open orbit so that the moon leaves the Earth orbit.

In a circular orbit, the total energy of the moon is $E = K + U$ , with $U = -2K$ ( virial theorem ). Since $E = -K < 0$ , the moon remains bound to the earth.

By halving the mass of the earth, the potential energy becomes half of its original value, i.e. $U = -K$ . The total energy becomes $E = 0$ , meaning that the moon is no longer bound to the earth. It will travel away from the earth in a parabolic path; as its distance to the earth increases, its speed will approach zero.

There is no longer an Earth, so the moon simply leaves. :-D

The orbital velocity along a circular path at a distance 'r' from earth is the same as escape velocity at the same distance if mass of earth is halved, the moon escapes from earth's gravitational field

The velocity of the moon as an object in circular orbit is

V_orbit=sqrt(GM/R)

The escape velocity of moon right after the impact is

V_escape=sqrt(2G*(M/2)/R)=sqrt(GM/R)

Hence, the moon will leave its orbit around the earth and, since the two velocities are equal, will eventually come to a stop.

-m-