Beginning of something new
Find the derivative of the function y = x x .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Moderator note:
Yes, this is the standard logarithmic differentiation approach. Bonus question: Do we still need to apply logarithmic differentiation if we want to determine d x 2 d 2 y , d x 3 d 3 y , … and so on?
Answer to challenge note: Not necessary. We already know the first derivative of x^x and can re-use that
Shouldn't the third line be
d x d l n y = d x d x l n x
? then
d y d l n y d x d y = l n x + 1
Log in to reply
i skipped that step and just took the derivate of lny with respect to y and showed it which was 1/y
Log in to reply
I'm not saying you skipped any step, I'm saying you wrote dy instead of d
Log in to reply
@Ka Kei Yeung – Yes, because that is implicit differentiation. when you take the derivate of lny you use the chain rule and take the derivate of y with respect to x which is 1 times dy/dx
Log in to reply
@Alex Kasantsidis – " Yes, because that is implicit differentiation. when you take the derivate of lny you use the chain rule and take the derivate of y with respect to x which is 1 times dy/dx" Yes by chain rule:
d x d l n y = d x d x l n x
d y d l n y d x d y = l n x + 1
y 1 d x d y = l n x + 1
Log in to reply
@Ka Kei Yeung – So i just skipped your 3rd step. I am sorry.
Log in to reply
@Alex Kasantsidis – No the skipping is fine, but not the dy instead of d in YOUR 3rd line.
Moderator note:
Correct. Can you type it out here? It's not entirely legible.
y = x x y = e l n ( x x ) y = e x l n ( x ) y ′ = ( l n ( x ) + 1 ) ( e x l n ( x ) ) y ′ = ( l n ( x ) + 1 ) x x
If y = x x
Use properties of logarithmic functions to expand the right side of the above equation as follows.
ln y = x ln x
We now differentiate both sides with respect to x, using chain rule on the left side and the product rule on the right.
y '(1 / y) = ln x + x(1 / x) = ln x + 1 , where y ' = dy/dx
Multiply both sides by y
y ' = (ln x + 1)y
Substitute y by x ^x to obtain
y ' = x^x(ln x + 1)
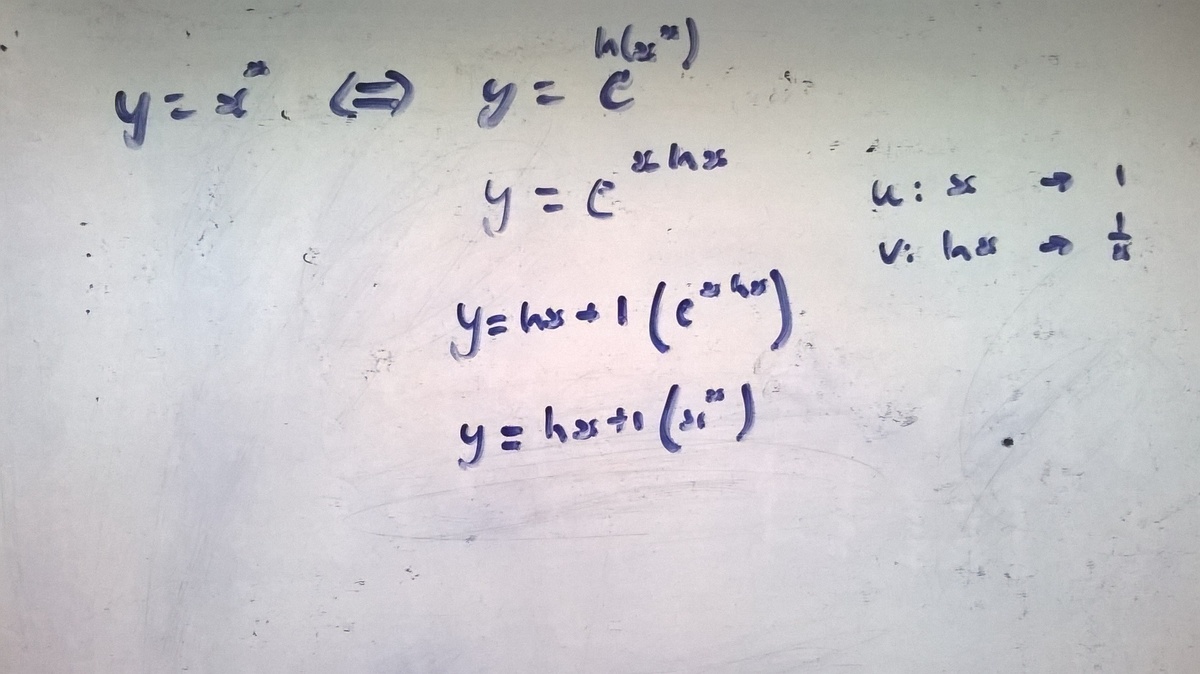
y = x x
l n y = x l n x
d x d y l n y = d x d y x l n x
using implicit differentiation you get
y 1 d x d y = l n x + 1
d x d y = y ( l n x + 1 )
recall y = x x
therefore
d x d y = x x ( l n x + 1 )