Descartes Sangaku : The stairway part 1

Geometry Level pending
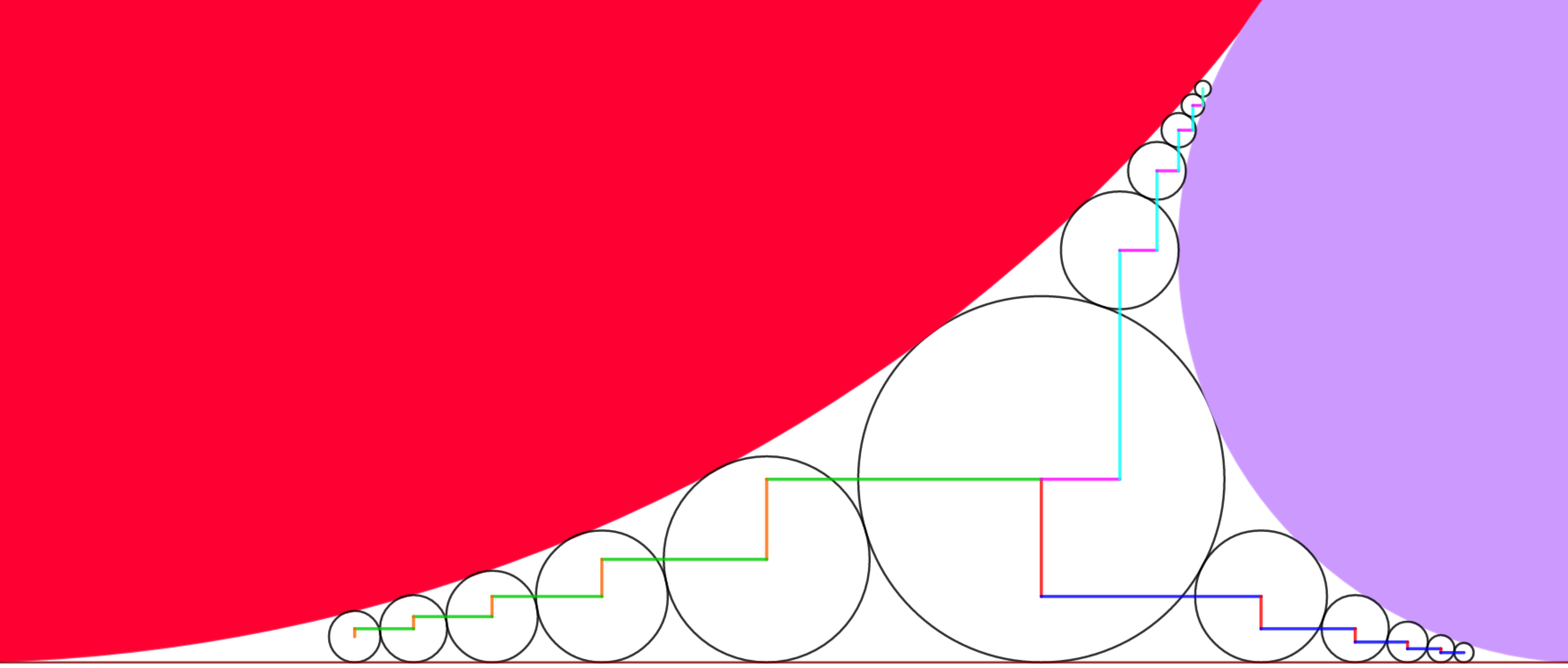
  • The diagram shows a red circle with radius 1 2 \boxed{\frac{1}{2}} and a purple circle with radius 1 8 \boxed{\frac{1}{8}} tangent to each other and mutually tangent to the same brown line
  • We inscribe a circle between the brown line, the red circle and the purple circle.
  • Then we pack the space with circles to the left, to the right and to the top.
  • At last we build 3 stairways by connecting the center of consecutive circles ; consecutive stairs are perpendicular to each other.
  • We consider the stairway built to the right side of the diagram. This stairway is composed of red vertical lines and blue horizontal lines.
  • The n t h n^{th} red vertical line is denoted as V n \boxed{\color{#D61F06}V_n} .
  • The n t h n^{th} blue horizontal line is denoted as H n \boxed{\color{#3D99F6}H_n} .

The question: Evaluate : ∑ n = 50 60 H n ∑ n = 50 60 V n \boxed{\frac{\sum _{n=50}^{60}\color{#3D99F6}H_n}{\sum _{n=50}^{60}\color{#D61F06}V_n}} , for n ≥ 1 n≥1 the answer can be expressed as a b \boxed{\frac{a}{b}} where a a and b b are coprime positive integers. Calculate a − b \boxed{a-b}


The answer is 12199.

Valentin Duringer by Valentin Duringer , 30, Belgium

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Valentin Duringer
Aug 19, 2020
  • First, let's calculate the sequence of radii of consecutive circles on the right side, starting from the central black circle. Using Descartes Circle's Theorem, we get the 6 first radii of the sequence:
  • 1 18 \boxed{\frac{1}{18}}
  • 1 50 \boxed{\frac{1}{50}}
  • 1 98 \boxed{\frac{1}{98}}
  • 1 162 \boxed{\frac{1}{162}}
  • 1 242 \boxed{\frac{1}{242}}
  • 1 338 \boxed{\frac{1}{338}}
  • We notice that the numerator stays the same, and we can rewrite the denominators and identify a pattern :
  • 18 = 2 + 16 ⋅ 1 = 2 + 16 ⋅ ( 1 ) \boxed{18=2+16\cdot 1=2+16\cdot \left(1\right)}
  • 50 = 2 + 16 ⋅ 1 + 16 ⋅ 2 = 2 + 16 ⋅ ( 1 + 2 ) \boxed{50=2+16\cdot 1+16\cdot 2=2+16\cdot \left(1+2\right)}
  • 98 = 2 + 16 ⋅ 1 + 16 ⋅ 2 + 16 ⋅ 3 = 2 + 16 ⋅ ( 1 + 2 + 3 ) \boxed{98=2+16\cdot 1+16\cdot 2+16\cdot 3=2+16\cdot \left(1+2+3\right)}
  • 162 = 2 + 16 ⋅ 1 + 16 ⋅ 2 + 16 ⋅ 3 + 16 ⋅ 4 = 2 + 16 ⋅ ( 1 + 2 + 3 + 4 ) \boxed{162=2+16\cdot 1+16\cdot 2+16\cdot 3+16\cdot 4=2+16\cdot \left(1+2+3+4\right)}
  • 242 + 16 ⋅ 1 + 16 ⋅ 2 + 16 ⋅ 3 + 16 ⋅ 4 + 16 ⋅ 5 = 2 + 16 ⋅ ( 1 + 2 + 3 + 4 + 5 ) \boxed{242+16\cdot 1+16\cdot 2+16\cdot 3+16\cdot 4+16\cdot 5=2+16\cdot \left(1+2+3+4+5\right)}
  • 338 = 2 + 16 ⋅ 1 + 16 ⋅ 2 + 16 ⋅ 3 + 16 ⋅ 4 + 16 ⋅ 5 + 16 ⋅ 6 = 2 + 16 ⋅ ( 1 + 2 + 3 + 4 + 5 + 6 ) \boxed{338=2+16\cdot 1+16\cdot 2+16\cdot 3+16\cdot 4+16\cdot 5+16\cdot 6=2+16\cdot \left(1+2+3+4+5+6\right)}
  • We can conclude : R n = 1 2 + 16 ⋅ ∑ k = 1 n k = 1 8 n 2 + 8 n + 2 \boxed{R_n=\frac{1}{2+16\cdot \sum _{k=1}^nk\:}=\frac{1}{8\:n^2+8\:n+2}}
  • Now, we notice that we can make a right triangle by using the center of two consecutive circles. Joining their center makes the hypothenuse, the blue and red lines are the legs of the triangle. This allows use to write this pythagorean equality:
  • ( R n + R n + 1 ) 2 = V n 2 + H n 2 \boxed{\left(R_n+R_{n+1}\right)^2=\color{#D61F06}V_n^2+\color{#3D99F6}H_n^2}
  • Since the circles of the considered sequence lie on the same line we can write ( R n − R n + 1 ) = V n \boxed{\left(R_n-R_{n+1}\right)=\color{#D61F06}V_n}
  • ( R n + R n + 1 ) 2 = ( R n − R n + 1 ) 2 + H n 2 \boxed{\left(R_n+R_{n+1}\right)^2=\left(R_n-R_{n+1}\right)^2+\color{#3D99F6}H_n^2}
  • Using the last result : R n = 1 8 n 2 + 8 n + 2 \boxed{R_n=\frac{1}{8\:n^2+8\:n+2}} and after doing some algebra we find:
  • H n \color{#3D99F6}{H_n} = = 1 ( 2 n + 1 ) 2 ( 2 n + 3 ) 2 \boxed{\sqrt{\frac{1}{\left(2n+1\right)^2\left(2n+3\right)^2}}}
  • V n \color{#D61F06}{V_n} = = 4 ( n + 1 ) ( 2 n + 1 ) 2 ( 2 n + 3 ) 2 \boxed{\frac{4\left(n+1\right)}{\left(2n+1\right)^2\left(2n+3\right)^2}}
  • ∑ n = 50 60 H n ∑ n = 50 60 V n = 12423 224 \boxed{\frac{\sum _{n=50}^{60}\color{#3D99F6}H_n}{\sum _{n=50}^{60}\color{#D61F06}V_n}=\frac{12423}{224}}
  • a − b = 12423 − 244 = 12199 \boxed{a-b=12423-244=12199}
1 Helpful 1 Interesting 2 Brilliant 0 Confused

Nice problem. If the question had been ∑ n = 50 59 \displaystyle\sum_{n=50}^{59} , I would have got it right. Doh!

Fletcher Mattox - 9 months, 3 weeks ago 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
 
from sympy import *

def f(n):
    if n == 1:
        r = Integer(1)/18
        x = Integer(5)/6
    else:
        r_1, x_1 = f(n - 1)
        r = A077591(n+1)
        x =  x_1 + 2 * sqrt(r_1 * r)
    return r, x

def A077591(n):
    """ works only for middle, small, large from left to right.
        n = 1 is really the 3rd circle """
    return Integer(1)/(8*n**2 - 8*n + 2)

r0, x0 = f(50)
r1, x1 = f(61)
delta_x = x1 - x0
delta_r = r0 - r1
print(delta_x / delta_r)


1
 
12423/224

Fletcher Mattox - 9 months, 3 weeks ago

Log in to reply

Hello friend, I'm happy you like the problem and you can still try part 2 and 3 or the last series i posted. I'll post my last series today, I'lll do 3 parts maybe. Anyway those will be the last problems I post for a very very long time

Valentin Duringer - 9 months, 3 weeks ago

Log in to reply

I did part 2 in much the same way as part 1. Part 3 looks a little trickier. I am sorry to see you leave, Valentin. Good luck!

Fletcher Mattox - 9 months, 3 weeks ago

Log in to reply

@Fletcher Mattox – For part 3 you need to do what young poeple were not taught to do...try, research, try again! See you in part 3 then!

Valentin Duringer - 9 months, 3 weeks ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...