Determine The Induced Charge
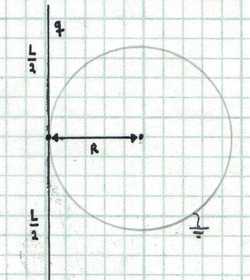 Consider a dielectric thin rod with total charge
q
=
1
μ
C
uniformly distributed over its length. The rod touches a grounded conducting sphere of radius
R
=
5
0
cm
as shown in the figure below. Find the charged induced in the sphere
in microcoulombs
if the length of the rod is
L
=
1
m
. The following integral may be useful:
∫
a
2
+
x
2
1
d
x
=
ln
(
x
+
x
2
+
a
2
)
+
C
.
Consider a dielectric thin rod with total charge
q
=
1
μ
C
uniformly distributed over its length. The rod touches a grounded conducting sphere of radius
R
=
5
0
cm
as shown in the figure below. Find the charged induced in the sphere
in microcoulombs
if the length of the rod is
L
=
1
m
. The following integral may be useful:
∫
a
2
+
x
2
1
d
x
=
ln
(
x
+
x
2
+
a
2
)
+
C
.
The answer is -0.88.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Eagerly waiting for your next problem..
how did you derive the expression for potential due to the rod becuase that is the real thing i have problem deriving ..so please just tell me how did you do it?
Why wont the induced charge be uniformly distributed?
I just cant figure out these problems involving double integration
Since the sphere is grounded, the electrostatic potential at every point on it and hence potential at center would be 0 .
Say, charge Q is induced.The induced charge would reside at the surface. Hence, the distance of center from every small charge d q
The potential due to induced charges at the center ( V 1 ) = ∫ 4 π ϵ 0 R d q = 4 π ϵ R Q
Also, the potential at center due to rod ( V 2 ) = 2 ∫ 0 L / 2 4 π ϵ 0 R 2 + x 2 q / L d x
Using 2 L = R , V 2 = 4 π ϵ 0 R q ln ( 2 + 1 )
Hence, total potential at center = V 1 + V 2 = 0
Thus, 4 π ϵ R Q + 4 π ϵ 0 R q ln ( 2 + 1 ) = 0
OR Q = − q ln ( 1 + 2 ) = − 0 . 8 8 μ C
i did in the same way as you did but while i was integrating i integrated the potential with lower limit=0 and upper limit=L and didnt got the answer right, is my way of doing it wrong?
Log in to reply
Note that he doubled the integral. So if you did the integral from 0 to L, then you must not double it, then you will get your answer..(you must get it).
Log in to reply
No he won't get it as for him, x is distance from lower end of rod, and for me it is from bottom end of rod. If x were distance from bottom,
V 2 = 4 π ϵ 0 q ∫ 0 L ( R − x ) 2 + R 2 d x
i did not double it
Did the same 😄
Let Q be the induced charge on the sphere.
Now,
Even though this induced charge is non-uniform ,
The potential due to this induced charge at the center of the sphere is still V 1 = R k Q
Also,
Potential due to the rod, at the center of the sphere, is given as,
V 2 = L k q l n ( sec α − tan α sec α + tan α )
Since the sphere is grounded ,
V 1 + V 2 = 0
R k Q + L k q l n ( sec α − tan α sec α + tan α ) = 0
Note that,
tan α = 2 R L and sec α = 2 R 4 R 2 + L 2
Substituting the values of tan α and sec α , we get,
Q = − L q R l n ( 4 R 2 + L 2 − L 4 R 2 + L 2 + L ) ≈ − 0 . 8 8 1 3 μ C