Dice Rolling Puzzle
 Two fair dice are rolled, and it is revealed that (at least) one of the numbers rolled was a 4. What is the probability that the other number rolled was a 6?
Two fair dice are rolled, and it is revealed that (at least) one of the numbers rolled was a 4. What is the probability that the other number rolled was a 6?
Note: You are not told which of the numbers rolled is a 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Answer is straight away 1/6 because occurrence of 4 on one dice doesn't add any information to it because both dices are independent of each other
Log in to reply
The problem here is that the dice are assumed to be indistinguishable at sight. If, suppose, one of them is coloured red and the other blue, then upon noticing that one of them shows a 4 , we would also notice that which one has the 4 . But that's not the case here. So, I think the problem should mention that the dice are indistinguishable.
If the dice are distinguishable, then indeed the probability is 6 1 .
A : One of the die shows a 4 (and you know which).
B : The other die shows a 6 .
P ( A ∣ B ) = P ( B ) P ( A ∩ B ) = 3 6 6 3 6 1 = 6 1
PS : Even I clicked 6 1 .
Log in to reply
not at all required,the question clearly mentioned that one of them showed a 4 and what is the probability of the other die showing 6.that means we have only one die infront of us we have to just predict the probability of the die infront of u showing 6.thats ofcourse 1/6.i could never accept the above answer.its completely illogical.
Is it not normally the default with dice throwing problems that the dice are indistinguishable, (as in the photo), but for the purpose of creating the sample space for analysis, considered as distinct? It doesn't hurt to mention it, but I don't think that it's absolutely necessary. Anyway, you've provided a good analysis of why the two scenarios lead to different results. :)
Actually in probability there is nothing as "similar or distinguishable". We are always expected to consider each item or object involved as distinct. eg-in problems where you have n red balls and m blue balls and other things,we need to consider each ball as distinct whether they are of same color or not.
I agree, see my comment.
yeah, I also applied same logic and clicked 1/6. Assumptions should be given in questions: Two dice are different, and exaclty one showed a 4.
[Update] please see this: http://math.stackexchange.com/q/884364/128946
Here, you have to take B as the condition already taken place I.e. occurrence of 4 on one dice and A as another condition.
Therefore, p(A/B) = (2/36)/(11/36) = 2/11
Here, you have to take B as" the condition already taken place "I.e. occurrence of 4 on one dice and A as another condition.
Therefore, p(A/B) = (2/36)/(11/36) = 2/11
Log in to reply
@Anuj Agarwal – The question is how you found out that one die had a 4 on it. The problem implied that you happened to see one of them, in which the case the answer would be 1/6. If you found out by asking someone "is there at least one 4 there", then indeed the answer is 2/11.
The problem is misleading.
They are independent, but this problem involves conditional probability. Look at this mathematically similar problem: I roll two fair dice and tell you that at least one of the dice shows a 4 , then ask you what the probability is that the other dice shows a 6 . Now there are 1 1 possible outcomes that result in at least one 4 showing, namely
( 4 , 1 ) , ( 4 , 2 ) , ( 4 , 3 ) , ( 4 , 4 ) , ( 4 , 5 ) , ( 4 , 6 ) , ( 1 , 4 ) , ( 2 , 4 ) , ( 3 , 4 ) , ( 5 , 4 ) and ( 6 , 4 ) .
Of these, there are only 2 outcomes where a 6 shows up, and hence you conclude that the conditional probability that given there is at least one die showing a 4 a 6 shows on the other die is 1 1 2 .
Log in to reply
I dissent with you Brian, if successes are independent they cannot be conditional. Suppose you have two bag with equally number of balls red and white you, lets say two on each bag one red one white, now take one ball of the first bag this event does not change the outcome of the extraction of the second bag, no matter if you do the extraction simultaneously or not.
The mistake, in my opinion is consider the space of probability as stated by Pranjal Jain , the fact the are taken simultaneously does not change the nature of the events, since they are independent in the first place.
Log in to reply
@Mariano PerezdelaCruz – The result of the throw of each of the dice is independent, but the conditionality is on the information we receive about the outcome. On the condition that one (and possibly both) of the dice shows a 4 , we are asked what the probability that the other die shows a 6 . This does not deny the independence of the throws themselves, but it does place a condition on our knowledge of the outcome. So in this way the independence of the act and the conditionality of the information we're provided can co-exist.
Log in to reply
@Brian Charlesworth – I still don't get it. What happens to the one side you don't count to get that 2/11? No, you still get 1/6 chances unless you pull out one of the numbers....say reroll if you get a 4 because the other dice is a 4.
@Mariano PerezdelaCruz – indeed, just by the fact of looking at them, even when they can not be distinguished affect the result, because now there's "the dice we saw first" and "the one we havent look yet", or a D1 and D2, so the convinations (X,4) couldnt exist anymore.
Log in to reply
@Jesus Frankenstein
–
why not? I don't understand why you could not roll a 2nd 4 just because the first dice is a 4.
They are still independent. Now if you say "reroll if you roll a 4" then yeah.
@Jesus Frankenstein – Jesus, I do not know by the context you are answering me or to other. My point is that once you disclose the result in one bag and the chances are equals in both bags you must reestablish the space of probability a this point. If the bags were of different composition of balls and you do not know from which bag came from you have a legitime argument, since you have not destroy the assumption of simultaneaty.
Log in to reply
@Mariano PerezdelaCruz – I think that the extent of the dissent voiced in the comments has demonstrated that the wording of the question left too much room for interpretation. I'm not sure if it would be worth changing the wording at this point; probably posting a new question with more precise wording would be preferable, something I may do later.
Log in to reply
@Brian Charlesworth
–
You are right Brian good wording is essential to understand the issues.
I, a retired naval architect and new in this forum, came just looking for leisure to spend spare time instead of sudoku.
I am amazed for amount of youngster very sharp brained around here, however their math skills not always are accompanied with a fair enunciate of questions ... the old fight at school Math vs English composition, but rigour is essential in math anyway.
Thinking about this particular problem, somehow make me remember the Monty Hall TV show with the car and the goats . I believe there thousand of controversial opinion on it I shall make a research on it.
Log in to reply
@Mariano PerezdelaCruz – Haha. Yes, I find this site more fun than sudoku as well. :) I too am impressed with the calibre of the young minds here; their love for mathematics and science is palpable, and they are very respectful of one another as well, (for the most part). Given that English is a second language for many of them, I am also generally impressed with the facility they have achieved with the language. However, even with native speakers ambiguities can crop up, in particular with the wording of probability questions.
The Monty Hall problem is one one of my favorites. I posted a variation some time ago that proved to be quite popular.
the language used here is incorrect... the probability is asked on for the One dice... and the answer given is based on both the dice....
This only becomes a conditional probability if none of the outcome has been known. Once the outcome of one dice is known, the outcome of the other is independent. The statement should be in future form so you don't distinguish one from the other.
Imagine that the other dice kept on rolling for 5 more minutes after the other stopped (just to exaggerate). While it rolls for 5 minutes, can you say the probability that it would show 6 is 1 1 2 ? Definitely no.
And why don't you count set (4,4) two times?
Log in to reply
@Talha Altaf – See my table below! 6×6... Do you see 4×4 two times there?
@Talha Altaf – But why would I need to count ( 4 , 4 ) twice? It's a singular outcome: the number 4 appears on each of the dice, and there is only 1 way that can happen. In the other cases the numbers are different so, for example, I count ( 1 , 6 ) and ( 6 , 1 ) as two outcomes.
Log in to reply
@Brian Charlesworth – Alright! Now does it make any difference to your sample space if I have two indistinguishable dies and I roll them separately in following way.
Event A: Roll dice number 1
Event B: Roll dice number 2
Now, if I say that among event A or B one outcome is a 4. Now what is the probability that the other outcome will be 6.
Is it exactly the same problem or a different one?
Log in to reply
@Talha Altaf – Yes, thats the same! And here also the probability is 1 1 2
Log in to reply
@Pranjal Jain – Ok. Now please point out my mistake.
Possible outcomes:
-
Event A appears a 4, Event B appears 1,2,3,4,5,6 = Total 6 outcomes
-
Event B appears a 4, Event A appears 1,2,3,4,5,6 = Total 6 outcomes
Hence Probability will be 2/12 = 1/6
Log in to reply
@Talha Altaf – One event of (4,4) is repeated!
Event A appears 4 and Event B appears 1,2,3, 4 ,5,6
Event B appears 4 and Event A appears 1,2,3, 4 ,5,6
No, it does not involves conditional probability. Even if they're identical, they're distinguishable because we have noticed the one that showing 4. Yes, they are independent.
Nope. You are duplicating outcomes. (4,1) is indistinguishable from (1,4) as the order of dice rolls is independent and indetermined (we don't know if we are shown dice A or B). There are 21 total unique roll combinations, of which 6 contain at least one 4. Of those 6, only 1 also contains a 6.
These are the possible outcomes here... 1,1 1,2 1,3 1,4 1,5 1,6 2,2 2,3 2,4 2,5 2,6 3,3 3,4 3,5 3,6 4,4 4,5 4,6 5,5 5,6 6,6
Log in to reply
@Chad Wallace – Are all of those outcomes equally likely? IE Are we as likely to see { 4 , 4 } as we are to see { 4 , 6 } ? If yes, would you say that the probability of rolling { 4 , 6 } is 1/21?
If no, what are the probabilities of rolling { 4 , 4 } and { 4 , 6 } ?
yes, I also thought the same
Right, I agree with Altaf. The question should be formulated differently.
Log in to reply
Two dice were rolled. 2/12 (for any number). "The other dice rolled" = 1/6. I don't care about the first die, but I'm an English teacher, with little time for these impressive formulae.
That is quite wrong. "You are not told which of the numbers rolled is a 4." There are 11 possibilities with a 4, and two of them also have a 6.
I believe the difference is that it us stated in the problem that one dice is 4, which means that it is not possible for both dices to be 4.
Log in to reply
No! It is a possible outcome! See Brian's solution.
Since the wording of the question does not specify that precisely one dice shows a 4 , it can be assumed that having both dice show 4 is still a possibility. This is the subtle but critical key to finding the correct answer to this question.
I do agree with Talha Altaf the probability is 1/6 since the rolling of the of the first dice does not condition the outcome of the second and is fully independent.
Log in to reply
| (1,1) | (1,2) | (1,3) | (1,4) | (1,5) | (1,6) |
| (2,1) | (2,2) | (2,3) | (2,4) | (2,5) | (2,6) |
| (3,1) | (3,2) | (3,3) | (3,4) | (3,5) | (3,6) |
| (4,1) | (4,2) | (4,3) | (4,4) | (4,5) | (4,6) |
| (5,1) | (5,2) | (5,3) | (5,4) | (5,5) | (5,6) |
| (6,1) | (6,2) | (6,3) | (6,4) | (6,5) | (6,6) |
So there are 11 equally probable outcomes.
Favourable outcomes are (4,6),(6,4)
So probability= 1 1 2
@Mariano PerezdelaCruz @Talha Altaf
Log in to reply
I dissent with you, the success are independent and you only can make them dependent if are establishing mutual information links. Besides the statement of the roll of dices was simultaneously it is irrelevant, since once you announce the result of the first dice automatically you break the statement . For practical computation you must scratch its result from the space of probability which is reduced just 1 to 6 . Past history does not count in probability as my teacher told.
Log in to reply
@Mariano PerezdelaCruz – the probability is asked for the second die or the other die...... so the answer should be 1/6 ... if the die are identical.. and of they are distinct..... then the answer will be 2/11............... as (4,1) and (1,4) will be treated as distinct sample spaces... same way as (4,6) and (6,4)
Log in to reply
@Ameya Patil – Ameya I do not know if I express my views correctly, my English is a kind of rusty.
Imagine we are looking for at least a 6 out of the two dices rolls. Taking the space probability matrix table from Pranjal Jain above, originally we see to have a probability of 11 out 36. But once the result of the first roll is announced you are forced to discard from the matrix all except one row or one column since that new scenario is the actual probability space 1 in 6.
The problem it could be treated as conditional probability if let say one dice A has only 2,4,6 and the other B has 1 to 6 as usual. Now after a first roll you say there is a 4 not telling from what dice come from now you can elaborate the new probability for getting a 6.
Log in to reply
@Mariano PerezdelaCruz – I have explicitly stated that.... the probability is to be found out for only 1 dice showing SIX... with 4 on the other Dice already considered .... so the sample spaces reduces to 11 from 36 ..... and if the Dices are distinct as BLUE and RED ... the Probability will be 1C1/11C1 + 1C1/11C1............ that is 2/11
and if the dices are identical then the answer is 1/6........
This problem (and its solution) is easier to grasp when considering a very large number of dice: Suppose you throw N dice, and you are told that of (N - 1) dice, none show a 6. The probability that the Nth die does show a 6 then approaches 1 as N gets larger.
Log in to reply
@Robert de Groote – I like this concept. It drives home the fact that, while the throws themselves are independent of each other, our analysis is conditional on the information we receive about the outcomes.
Log in to reply
@Brian Charlesworth – Yes, but how would you characterize this information? It seems like it has something to do with the number of ways to select the N - 1 dice that were 'revealed' from the group of N dice...
Since it was not specified which group of N - 1 dice was referred to when revealing the absence of sixes, there are N possible ways to 'hide' the information regarding the Nth die.
If we were told that the first N - 1 dice did not show a six, then the probability for the Nth die showing a six would have been 1/6, since there is only 1 way of hiding the outcome of the Nth die.
Disclaimer: I know there is a relationship between the nr. of combinations and entropy / information, but I have no clue whether what I'm concluding here makes any sense.
Log in to reply
@Robert de Groote – You're right; this brings back memories of a statistical mechanics course. If we roll a die N times and notice that the first N-1 rolls yield no 6's, that doesn't change the odds of rolling a 6 on the Nth roll. But if N dice are rolled simultaneously and we are told that a random sampling of N-1 dice yielded no 6's, then the odds that the remaining die is 6 increases with N. But if we took a second random sampling of N-1 dice and still there were no 6's, then the odds that any of the rolls yielded a 6 would diminish with N, making us suspicious of the fairness of the dice. The information can be 'hidden', as you say, by random sampling, but only up to a point. I think I'll have to fish out my textbook to see if I'm actually talking sense here. :)
Alright! Now does it make any difference to your sample space if I have two indistinguishable dies and I roll them separately in following way.
Event A: Roll dice number 1
Event B: Roll dice number 2
Now, if I say that among event A or B one outcome is a 4. Now what is the probability that the other outcome will be 6.
Is it exactly the same problem or a different one?
no, because the 4 on one of the dice is already rolled, you don't have that 2nd set of numbers. Now, if they had asked to roll double 4s, or the probability of rolling a 6 AND a 4 at the same time.... But they didn't. They said you already rolled a 4, and want to know your chances of getting a 6.
I thought exactly like this so I fully agree with you Pranab Jain. Perhaps someone can simulate the dice throws 10000 times and calculate the relative frequency of getting a 6 given one of the dice shows 4? Just to settle the argument ;)
Log in to reply
@Magne Myhren – If you tried to solve this via a simulation then they key thing to decide is how the four is revealed. If you have a magic "four radar" and would always notice a four if one were present then the answer would be 1 1 2 but if you noticed numbers with an equal probability (e.g randomly seeing one of the two dice) then you would get 6 1 . The second seems more realistic.
The argument has a flaw: the case (4,4) contains two fours, so this case is actually counting as 2 cases. Thus, there are actually 12 equally probable outcomes and the probability is actually 1/6. This is highly reminiscent of the problem that states: you have one card which is red both sides and another card which has one red face and one blue face. The probability of the card being red both sides is actually 2/3 upon flipping a red face.
In your analysis Is think you should instead say that you saw one of the twelve fours (not one of the eleven outcomes) so it should be 1 2 2
I think the answer should be 1/6 because the question is about the probability of the "other" die showing "6" and not about the probability of having a pair (4,6) when the result of rolling one of the dice is known to be "4".
Log in to reply
I agree with Grant. The question is worded incorrectly. The answer should be 1/6
I guess we have a wording issue here. If we rolled two dices together, we have 36 possibilities, two of them are (4, 6) and (6, 4). So, if someone tell us we already have a 4 and the other is already rolled, yeah, we have conditional probability and the answer should be 1 1 2 .
But if we rolled one, it shows a 4, them we will roll the second, we just have 6 possibilities, one of them is a 6, so the answer should be 6 1 .
When I read first time, I assumed the 2nd way, so I answered 6 1 . Now, I read again, again and again but still cannot choose which the 2 ways of understanding is the correct one. I woud prefer a better stated problem.
(¬_¬) I wonder how is it possible for you to "... noticed that one of the dice shows a 4..." without knowing which one was it.... I would prefer the following problem...
Two fair dice are rolled together and your friend tell you that one of the dice shows a 4. What is the probability of the other die showing 6?
Log in to reply
Much better. I think that's what the problem intended.
Log in to reply
Would make no difference, they are independent dice 1/6 is correct. One die cannot affect the other.
@Sandeep Bhardwaj Welcome back!
Log in to reply
thank you. @Calvin Lin @Pranjal Jain
Log in to reply
@Sandeep Bhardwaj I have tried your problem "Circular stations ... Strange!!" and have a few questions about it. (If I dispute the question to ask for clarification then I forfeit the right to answer the question, so I thought I would ask you here first.)
Does the train start at one of the stations, and then must visit 3 other stations before returning to the original station? Or does it start in between stations, and then must visit 3 stations before crossing the original starting point? Also, are we to assume that stations 1 and 10 are considered adjacent? Thanks in advance, and welcome back. :)
EDIT: I just figured it out, so no need to reply. It worked when I assumed that the 'starting point' was between stations and with stations 1 and 10 being considered adjacent. Good problem. :)
Log in to reply
@Brian Charlesworth – Thank you :)
Log in to reply
@Sandeep Bhardwaj – Answer is straight away 1/6 because occurrence of 4 on one dice doesn't add any information to it because both dices are independent of each other
Log in to reply
@Talha Altaf – Try to make 6×6=36 combinations and count it then.
If it had said you're told one of them is a 4, as opposed to you seeing the 4, then this would be right.
Log in to reply
Yes, I think that's the key. I translated the given problem into the scenario you describe in order to solve it, thinking that they were equivalent. The translated version leaves less room for interpretation, while the wording of this question is a bit tenuous, which has given rise to a, well, dynamic discussion. :) At this stage I'm not sure if it would be worth changing the wording; I think that the benefits of having raised a controversy and prompted a discussion outweigh the issues of clarity in the present wording, (if that makes any sense). Perhaps I'll post a question more in line with your scenario in mind and see if the controversy dies down.
Log in to reply
its quit wrong because two dice r rolled at same time one of them shows 4,,, so the probability of 6 for another dice is 1/6.
Log in to reply
@Ismail Karimi – If you know that one of them is a 4 but you don't know which one, it changes the possibilities.
Log in to reply
@Chelsea Saunders – Right. But the use of the word "the" (being specific) differentiates one from the other.
@Chelsea Saunders – If one die has a 4, than the other die is clearly a different die. Because the two dice are independent of each other, the odds of a 6 go from two chances at 1/6 odds to one chance at 1/6 odds. The information that one die, no matter WHICH die it was, had a 4 on it serves no purpose except to tell us that it clearly was not that die.
By keeping in mind the information First dice shows 4 and the other can show 1,2,3,4,5 or 6 So the sample space become { (4,1) (4,2) (4,3) (4,4) (4,5) (4,6) } There fore P(E) = 1/6
It's like throwing the dices one at a time and thus independent. Though they were rolled at the same time, the first would have no effect on the outcome of the other. The answer should be 6 1 .
For the answer to be 1 1 2 , the statement and the question should be rephrased. The problem should have been written like this:
Two fair dice are rolled together, if one will show 4. What is the probability of other will show 6?
See the difference?
Since is revealed that one of the dices shows a four, you have identified one of them. So the probability that the other shows a 6 is a straight 1/6.
Only language is responsible for all of this controversy. Put 'only ' before one and then all is well...!!.
The two events are completely independent of each other. Whether you roll two dies or ten dice, the probability of turning a given number up in fair die will always be 1/6. This is not like some kind of card game where the occurrence an event will definitely have an effect on the occurrence of the next event.
There's another good discussion of a problem similar to this here: http://math.stackexchange.com/questions/884364/two-dice-thrown-one-comes-up-6/884396
It matters a good deal on what rules the other person is following when they tell you that there is a 6. Are they randomly choosing one of the dice to reveal its value? If so, then the probability of another 6 is 1/6. Or are they only going to reveal when you've rolled a 6, and never another value? In that case it's 1/11. The situation changes the sample space of events (a single event being the roll of the dice and the possible reveal of information).
Log in to reply
Yes, precisely. Because of the independence of the two events, I clicked 1/6 but it showed wrong, which it shouldn't be.
The way in which the question is worded does not correspond to the answer of 2/11. I understand the rational for the answer however, it clearly stately that one of the dice IS a four. If it suggested that one of the two dice WOULD be a four, then you could surmise all of the probabilities and combinations of both dice in which there would be a 2/11 chance that there was a six rolled. If one die is already a 4, then that suggests that the OTHER die is the six, regardless of whether it's die a or die b. It specifically refers to the OTHER die being a six which would negate the necessity to run the probabilities of both dice. If the one die has already landed on 4, then that should only leave the probability of one die to roll a six which would be a 1/6 chance.
Log in to reply
You made the assumption that you knew which one of the dice is a 4.
You can perform a simple experiment using two coins. Flip them. In the scenarios that one of the coins is a Head (and so it is revealed that one of the coins is a head), what is the probability that the other coin is also a Head? Is it 2 1 ?
I would like to say that there's mistake in the question itself. If the question said " What is the probability of two dice (rolled together) shows 6 given that one of the die show 4?". The answer is 2/11 However, the question does not mention it appropriately ("it is revealed that one of the numbers rolled was a 4"). Thus, it mislead everyone and result the perspective that the other die rolled separately. Cmiiw
the probability is asked for the second die or the other die...... so the answer should be 1/6 ... if the die are identical.. and of they are distinct..... then the answer will be 2/11............... as (4,1) and (1,4) will be treated as distinct sample spaces... same way as (4,6) and (6,4)
This is not a conditional probability. They're independent. When you "noticed that one dice shows a 4", you have distinguished that particular die from another, even if they're same color, and there's no chance that the die will show another number. It's very different case with the probability of one dice shows 6 where the other will definitely showing 4 without telling which one, like what you try in your solution.
Log in to reply
But you didn't "notice" anything. You are told of one 4, and now you are asked what the chance is of a 6 joining it.
When cases where B occurs is 6 out of 36, out of which A occurs is 1, therefore P(A&B) should be 1/36, and probability of B i.e., P(B) is as said earlier 6/36 which is equal to 1/6, therefore P(A/B) should be equal to (1/36)/(1/6), which is 1/6 since both dice are independent of each other the result of one dice will not effect the other, even after applying the formula.
The answer should actually be 1/6.
Instead of 11 cases, the case with (4,4) is counted twice because the visible dice can represent either 4.
Thus, (2/36)/(12/36)=1/6, which is the answer
Log in to reply
The (4,4) case is NOT counted twice, because that's only ONE case, and NOTHING was "visible".
I think the line "you noticed that one of the dice shows a 4" indicates that you have identified a die that shows 4. Thus the probability that the other die shows a 6 is 1/6. Because we have already identified the die that shows 4. This is different from the tradition conditional probability when the only information we only know is that one die shows 4 . We now know that one die shows 4 and also the die that does it.
The solution provided only blindly applied conditional probability without properly stating the events that were of interest.
Log in to reply
There is no such line. You didn't "notice" anything. Reread it.
Your solution is wrong . the correct answer is 1/6 as the both die are independent , there is no effect of the other die showing any number.
Log in to reply
Except nothing was shown. You are merely told of a four among them.
If i do this experiment 66000 times i would be willing to bet you that the OTHER die would show a 4 closer to 11000 times rather than 12000 times. It is 1/6. Bayes can be taken to ridiculous extremes sometimes.
Log in to reply
I'm guessing you have NOT done this experiment 66000 times, then?
No this is wrong. It is 1/6 because they are 2 separate, fair dice. It doesn't matter what the "first" dice is, the question only asks what is the probability that the "second" dice is 6. They are not correlated so it is just a question of "what is the probability of rolling a 6 on a fair 6-sided dice?" which is 1 in 6 because only one side is labeled 6 and there are 6 total sides. THE TWO DICE ARE NOT CORRELATED SO THE FACT THAT ONE IS A 4 IS IRRELEVANT.
Log in to reply
You erred. You should not assume the 4 was the "first" die, just that it is ONE of the two dice. It could be either one, the first OR the second. Or both.
The answer is 1/6. While the problem is stated in a way that seems to assume conditional probability, there is no plausible link that would allow one die to influence the other.
Therefore they can only be independent, and the answer MUST BE 1/6.
Log in to reply
It is not that "one die influence the other".
Instead, you are updating your beliefs based on the information that is given.
Please, people. Think. You are rolling two INDEPENDENT, fair dice. There is no way specified for one die to influence the outcome of the other.
Some people are assuming that the state of one die is conditional upon the state of the other, but we actually have NO reason to think so.
So there is no dependency, and no conditional probability. And Bayes has no place here at all.
The answer is 1/6.
Log in to reply
Except that's not what the question was asking. Suppose we know there was a 4, but we don't know which one was a 4. What is the chance there is also a 6? There are two ways to get a six, out of the 11 ways to get a four. We are ignoring all other possibilities, such as (3,5), because that didn't happen, because we got a 4.
Log in to reply
NO, once you know one die is a 4 there is only 1 die left to be 1,2,3,4,5 or 6. It doesn't matter whether the known 4 was first or second. It is only "first" in the sense that it was the first one looked at. They are not entangled, so like the cat in a box, until it is revealed, the other die has 6 possible states. There are obviously not 2 ways to get a six if one die IS already a 4.
Log in to reply
@Hugh Fletcher – You can actually simulate this by tossing 2 coins.
Toss 2 coins repeatedly.
If at least one coin is a Head, that's a valid outcome.
Out of all of the valid outcomes, what is the experimental probability that the other coin is a Head?
Is it
2
1
,
3
1
,
3
2
? Why?
one dice is irrelevant. there are six sides to a die so its one in six that it will show
Log in to reply
It's very relevant. Every other number has two ways to show, but there's only one (4,4).
Sorry people but problem is wrong.. as written.
The problem sates that two dice are rolled.
So you have two dice on the table each showing a number (1-6)
You are told that one die shows a 4 (lets assume you cant see them)
You are then asked what are the odds the OTHER die shows 6?
There are only two dice and you have been given the results of one, and been asked to consider the remaining (singular) die's probability of being a 6.
As it is a singular die, rolled fair, the probability is 1/6.
And this is where the language comes into play.
As the problem uses the word 'other', the clause "You are not told which of the numbers rolled is a 4." becomes irrelevant.
Regardless of if the die showing 4 is die A or die B, the use of 'other' immediately singles out the remaining die,(be it B or A). The probability of a single roll is 1/6.
Log in to reply
You can perform a simple experiment using two coins. Flip them. In the scenarios that one of the coins is a Head (and so it is revealed that one of the coins is a head), what is the probability that the other coin is also a Head? Is it 2 1 ?
Maybe 2/11 is mathematically correct, but it's not realistically correct. If you throw one die you have 1/6 chance that you get 6, because you can get one of 6 possible outcomes. It doesn't change no matter how much dice you roll along with it - every single one of them will have exact same odds for being 6. Correct math is clearly wrong - adding one dice that's physically unrelated to first one doesn't miracoulusly increase odds of getting 6 from 11/66 to 12/66.
X = die known and Y = die not known The possibilities are (4,1), (4, 2), (4,3), (4,4), (4,5), and (4,6). Six possibilities and only one (4,6) includes a six, so the probability is 1/6.
Log in to reply
Knowing that "(at least) one of the dice is a 4", is very different from knowing that "the first die that we threw was a 4".
If we are considering this as "positive outcomes / total outcomes", then the 6 events that you described do not have equal probabilities, because it is much more likely to get a (4,6), then it is to get a (4,4). To "equalize" the probabilities, we have to include the remaining 5 cases of (1,4), (2,4), (3,4), (5,4), (6,4). This then makes the final probability 2/11.
I Think the wording of that question is awkward and causes the person to answer wrong unless the read it a few times. For example why write it was reveald that one of the numbers rolled was a a 4?
Simply ask when rolling two dice at the same time what is the probability the second dice is a 6, given the first dice was a 4? I bet more people would get the correct answer!
Log in to reply
That is the intention.
Knowing that "(at least) one of the dice is a 4", is very different from knowing that "the first die that we threw was a 4".
However, most people do not make this distinction clear to themselves, when trying to answer probability questions.
is it better to ask if 2 dics are thrown , what is the chance it will land a 4 followed by a 6 ? that will be 1/6 X 1/6 = 1/36 ? am i missing something here ?
Log in to reply
Yes, you are. In probability, the way the questions are phrased are extremely important. In particular, these 2 questions talk about different scenarios
-
(The current question) Given that one of the dice is a 4, what is the probability that the other dice is a 6?
-
(Your interpretation) Given that the first dice that landed is a 4, what is the probability that the latter dice that landed is a 6?
Note that the answer to 2 is 1/6, and not 1/36.
Aren't the chances of the 2nd dice being a 6 irrelevant of the other dices result? Regardless of what dice one gets, the chances of dice two being six remain 1/6. The question doesn't actually ask what are the chances of dice two being 6 and dice one being 4.
Log in to reply
There are 2 distinct questions:
-
(this question) Given that (at least) one of the dice is a 4, what is the probability that the other dice is a 6?
-
(your question) Given that the red (or first thrown) dice is a 4, what is the probability that the blue (or second thrown) dice is a 6?
Do you see why "knowing the first" vs "knowing one of them" is a different question?
I would assume that the two rolls's odds of a specific value were independent of each other, as the dice would not be working together in a James Bond-esque league to try to change the odds of a six.
Say I tossed a coin (let's just say it was a 50/50 chance for heads and tails). I would have a 50% chance of flipping a head. If I were to flip another coin (obviously with identical conditions), I would not suddenly have a 25%, 44%, 15%, 73%, or any other percentage chance of throwing a head. I would have the same 50% chance each time, as each coin in no way affects the odds of the throw of the other. The odds of me flipping heads on a coin will always be 50% (again, assuming it's not rigged), no matter how many times I throw it. This is why, if you flipped a coin one hundred times, you should generally get heads about half the time. The same rules apply here, only 1/2 is changed to 1/6. If I throw two dice, each dice individually has a 1/6 chance of rolling a 6- NOT a 2/12 chance for both. The two dice are independent, so I have two chances at 1/6 odds. However, because apparently one of the dice rolled a 4, that is one of my chances, and so I am left with one 1/6 chance.
They are independent variables. The probality of the second one being 6 is unrelated to what the first one is. Conditional probability only applies if you have not rolled either dice. Once the first dice is rolled, the probability that the other dice being 6 is unrelated ot the first dice being a 4, or any other value. I guess you could maintain both dice are rolled simultaneously. So the probability changes simply based on whether you roll them together or separately. Odd, don't you think?
Log in to reply
The error in your thinking is "Once the first dice is rolled, the probability that the other dice being 6", because there isn't a "first dice". These dice are indistinguishable.
If the dice had (say) different colors, and we said that "the red dice is a 4", then yes the probability that the green dice is a 4 is 1/6".
I will explain why authors of such puzzles are mistaken. The answer is 1/6. Where it becomes confused is this: you mention that there are 11 possible cases, however actually in reality there are 12 possible cases. The first dice is 4 and the second dice is 4, is one case that you consider, but you don't consider the second dice be 4 and the first dice be 4. They should be counted as 2 possibilities rather than one since you count 1-2 and 2-1 as 2 different outcomes.. think about it
Log in to reply
What you say doesn't make sense. Whichever way you count, (4,4) will always be counted as one outcome. Think about it, if you're told that both dice showed a 4, then the person who told you so has fixed the individual outcomes of each die for you. Whereas if you're told that one of the die showed a 4 and the other a 3, then he hasn't fixed the individual outcomes. Either one of them could have had a four. ONCE you fix the die that showed the 4 (2 ways of fixing that), the die that showed the 3 gets fixed.
In our case, someone has told us that one of the die showed a four. If the other die was 6, for example, there are 2 distinct outcomes of "the throwing of 2 dice experiment" that could lead to someone telling us that one die is a 4. But, if the other die also was also a four, then there is only one distinct outcome of "the throwing of 2 dice experiment" that could make someone tell us that one die is a four.
Poorly worded question. The odds that when you roll a 4 on two dice, the other number you rolled will be a 6 is 2/11, but if two dice have been rolled and you know one is a 4, the odds the other is a 6 is 1/6, just like if you flip 50 heads in a row, the odds the 51st will be a head is 1/2
Log in to reply
Note: The difference with your example is that "the first 50 coins are heads".
If you flipped 51 coins, and all that you know are some 50 of them are heads (but not which 50), then what is the probability that all 51 are heads? Hint: Think of the relevant probability space.
Doesn't this assume that the roll of one die is conditioned on the roll of the second? If they're independent, that's not true. I'm missing something here. What is it?
Log in to reply
It does not assume that the rolls are conditional (and they are not conditional).
I'm guessing what you're missing is understanding how the sample space is restricted when given additional information of "(at least) one of the dice shows a 4".
A proof that 2/11 is incorrect; All probabilities must add up to 1, and the question could equally be worded to ask the probability of the other die being 1,2,3,4 or 5 , instead of the stated 6, so there are 6 possible outcomes for the second die:
Suppose Probability of the other die being 6 = 2/11 as claimed Probability of the other die being 5 = 2/11 Probability of the other die being 4 = 2/11 Probability of the other die being 3 = 2/11 Probability of the other die being 2 = 2/11 Probability of the other die being 1 = 2/11 Sum of probabilities =12/11 NOT 1 This is NOT equal to 1 so is in error. The only possible answer is 1/6. Equally the known die could be 1,2,3 5 or 6 without changing anything.
The dies are independent, This is NOT a conditional probability. The error in the table is that, once you take both orders, 4,6 and 6,4, you have to include the 4,4 twice, it could be 4a4b or 4b4a.
The same fallacy occurs in the later problem concerning a boy born on Tuesday. The actual day is irrelevant and any other specified day of the week would give the same answer, so multiplying the given answer 13/27 by 7 should produce 0.5. It actually produces 91/27 which is a nonsense. The day of the week a boy is born cannot affect the sex of the sibling.
Some erroneous solutions have missed the fact that if two boys are both born on Tuesday it doubles the chance that you will be told that one child is a boy born on Tuesday for the tuesday-boy/tuesday-boy combination.
Knowing one die does not affect the other independent die and the application of Bayesian stats is totally inappropriate. Equally, Knowing the day a child is born does not add any information concerning the sex of a sibling.. .
Log in to reply
Sorry, For the Boy-problem, multiplying the answer (13/27) by 7 should equal 3.5 then taking the average, i.e. dividing by 7, should equal 0.5, since we know the overall probability without knowing the boy's birthday is 0.5.
Suppose Probability of the other die being 6 = 2/11 as claimed
Probability of the other die being 5 = 2/11
Probability of the other die being 4 = 2/11
Probability of the other die being 3 = 2/11
Probability of the other die being 2 = 2/11
Probability of the other die being 1 = 2/11
Sum of probabilities =12/11
I disagree with "Probability of the other die being 4 = 2/11". The probability is actually 1/11.
If you look at the above chart, you will see that there is 1 positive case out of 11 total cases.
The sum of the probabilities is then 11/11 = 1.
In particular, note that there is only 1 way to get a (4,4), especially when we fix the order of (say) a (red dice, green dice). Similarly, when we fix the order, there is only 1 way to get a (1, 4) and 1 way to get a (4, 1), which gives us 2 ways to get a { 1 , 4 } (Notice that I switched the bracket notation from ordered set to unordered set).
Log in to reply
You fail to notice that you might be told about one or the other 4 in a 4-4- case, so it comes up twice. There are two ways to know you have a four, you can be told about either. Once you are told about one die, whether it be 1,2,3,4,5 or 6 there are only 6 options for the other one, not 11. In total there are 6 options for each die, 6x6 = 36 options in total. How can you possibly get 11 options for the second die when you only have one die left to roll and the first one is already fixed at 4? If you know the column is 4 you just redraw the diagram to show the unknown row with 6 alternatives to go with the 4. And vice versa if you have ben told about the 4-row. There is exactly the same fallacy in the boy-born-on-Tuesday problem. The Tuesday information is irrelevant to the sex of the second child. In this problem, the number on one die does not affect or limit the number on the other. Looking at the diagram for the puzzle, if you are told about the 4-in the down column, you just eliminate the other 5 columns and there are still 6 entries in the 4 across row, and vice versa. That knowledge does not cut the four out of the other die.
Log in to reply
@Hugh Fletcher
–
But then your events do not have equal probability. To be clear,
the probability that we are in the
(
1
,
4
)
case and are informed about the "first" 4 is
3
6
1
,
the probability that we are in the
(
4
,
4
)
case and are informed about the "first" 4 is
7
2
1
.
the probability that we are in the
(
4
,
4
)
case and are informed about the "second" 4 is
7
2
1
.
So, we either have 11 equally likely outcomes, or 12 differently weighted outcomes and have to account for that in the later half of your analysis.
So do I disagree, about 2/11, that is my point. If you know one die is 4 you only have 6 options for the other, not 11, they are all1/6, not 2/11.
It is a quirk of English that many native speakers cannot get right, but the singular of dice is die. One die, two dice. I got the answer wrong, so I have to console myself by correcting grammar.
This problem is wrong. You mean to ask what is the probability that the sum is 10 if one of the dice is already landed on 4.
Unfortunately this is a trick question which is the only reason the answer is 2/11 and not 1/6 (which is what it should be based on the info above). How to tell it is a trick question? Well the category is combinatorics... that is really the only hint that the true answer is 2/11, no math gets you to this result either :D
Log in to reply
It's not a trick. Why should it be? Math is not about trickery.
Like seriously? Its clearly mentioned that 1 die's result is 4 so we just need to talk about the die that remains, so its answer must be 1/6 ????
Log in to reply
Except that we don't know which die remains. We know there is a 4, but we don't know which is the 4.
If you already know that one die has shown 4, why are you incorporating another die to have 4 in your sample space. Its already known that one particular die has 4 so why would u take those two (1,4) and (4,1) in your sample set? Tell me @pranjal is it not sure as to which die will show 4?
Log in to reply
No, not "one particular die", just one die. We have no way of knowing which die is a 4, just that there is one.
After thinking about it, if only one die shows a four, it's 1 in 5. So I was wrong earlier. It is a crap clumsily worded question, but I can't see an easy way to describe the 2/11 situation that would avoid being able to select either of the (4, 4) dice. Really, though, since both the left and right (4, 4) dice can be chosen, the answer really should be 1/6.
Log in to reply
The problem is clearly phrased. You might be approaching it with a pre-conceived notion of what it is asking for, instead of reading the question carefully.
There are 5 (first dice is 4, second dice isn't 4) + 5 (first dice isn't 4, second dice is 4) + 1 (both dice are 4) outcomes available, of which 2 of them are the positive outcome that we're looking for.
It didn't say ONLY one. It said "one". If you're in an all-girl class, is one of you a girl? Yes: you. Or your colleague, for example.
Imagine, for a moment, that the dice are actually colored Red and Blue. Would you agree that, if I saw that the Red die rolled a 4, there would be a 1/6 chance the Blue die would be a 6?
Now, let's say I give a Red and Blue die to a colorblind man. He rolls them, looks at the Red, and sees that it is a 4. Now, he can't tell the dice apart, because he's colorblind. But, the fact that he is colorblind does not change the fact that the Blue die has a 1/6 chance to be a 6.
The above scenario is equivalent to your problem.
See, the mistake in logic that you made was counting the (4,4) as a single case. (4,4) is actually two cases - (4,4) revealing die 1, and (4,4) revealing die 2. Therefore, there is a 2/12 chance that the second die is a 6, which simplifies to 1/6.
Should you argue that the dice are indistinguishable, and that thus both cases of (4,4) are one, then you cannot treat (2,4) and (4,2) as different cases.
Log in to reply
I agree that in your "Red and Blue" scenario, the answer is 1/6. However, that is a different question from what is asked.
-
(this question) Given that (at least) one of the dice is a 4, what is the probability that the other dice is a 6?
-
(your question) Given that the red (or first thrown) dice is a 4, what is the probability that the blue (or second thrown) dice is a 6?
Do you see why "knowing the first" vs "knowing one of them" is a different question?
The events that were listed out were events of equal probability, as opposed to events of distinct outcomes. Yes, you are right to say that (4,2) is indistinguishable from (2,4). However, in order to count the probability as "positive outcomes / total outcomes", we have to use equally likely outcomes. In this case, (4,2) is twice as likely as (4,4), which is why we had to count it twice.
Consider another scenario. There is a hat with 1000 slips of paper, where 999 are indistinguishable and say "Lose", and 1 of them says "Win", then what is the probability that we pick 1 slip and "Win"? Given that there are only 2 distinct outcomes, is the probability 1/2?
Note that it is the probability of (4,4) occurring that is important. It doesn't matter that we could split it into 2 subcases of "revealing first" vs "revealing second", whether it's with equal probability of with a biased probability. They ultimately give the same result in the calculation of P ( A ∩ B ) .
Log in to reply
If Calvin Lin says so, it must be true.
Thanks for the explanation. I'll know for next time, I guess.
(4, 4) is only one case: both dice turn up 4. Nothing is revealed, just that we are told that at least ONE die is a 4. There are 11 ways to do this, since the dice are two separate objects.
Question says "one of the numbers rolled was a 4". We must exclude (4,4) as a possibility since two of the numbers rolled would be 4s. This leaves 1/5 as the actual probability.
Log in to reply
You are only told that one of the numbers is a 4. You are not told anything about the other number.
Log in to reply
We know that the other number is not 4, because we are told that ONE of them is 4, not both, just one.
Log in to reply
@Stephen Lawless – That doesn't mean ONLY one. It's just means there is a four among them. If you have a boys-only party, isn't one of you a boy? You, for example. Or your first guest.
I cannot see why the answer is 2/11. The two dice are independent.
Log in to reply
Here is an experiment that you can perform at home:
Flip 2 (independent, fair) coins repeatedly and record the outcomes.
Consider only the instances when at least one of them is a head.
What is the proportion of these instances where the other one is a tail?
Yes they are, but the question is different from what you think. You might be thinking it's, "If the first die is 4, what is the probability that the other is 6," but that's not it at all! Either one could be 4.
You have assumed both the dice to be different but actually they are identical, so answer wil be 1/5
Another poorly phrased question. Two dice are rolled and one is shown to be a '4'. What are the odds that the second is a '6'? That would be '1/6' unless you give us some reason to think that there was something more involved in the die revelation process than simply revealing the result on the first die. You need to say something like "a person looks at both dice and says 'at least one of the two is a "6"'"
Log in to reply
Try again. Nothing is "shown"; instead, you it is "revealed" that one of the numbers is a 4. Which one is a 4 is NOT revealed. If I reveal to you that there is a dog at the park, did I have to show you the dog first? Is that the only way to reveal something?
I like your explanation.
The issue I had was when it said "one of the numbers rolled was a 4" which I took to mean exactly one of the numbers rolled was a 4, which excludes 4,4. Making the probability 2/10 or 1/5 :/
Is called free dice, should we need
We should. >4
BULLSHIT, it's 1/6, if one die is a 4 then there are only 6 sides in play and only 1 is a six. EOS
I figure that initially.. the chance of either 4 or 6 coming up on the die is 2/12 chance. The event of knowing that a die definitely landed a 4 changes the probability of the other die being a 6 by 1. Now the prob of the die being a 6 is 2/11
(There is 2 chance for 1 die to b a 6 because theres 2 die being rolled but now only 11 chances of one of the die actually falling on a 6)
Classic case of over-thinking a problem.
The dice are fair, and they are ALSO independent.
Therefore, the number on the first die is 100% irrelevant to the number on the second, which, because it is fair, has exactly a 1/6 probability of coming up 6.
The answer is 1/6. Any other answer is nonsense, and neglects to account for the independence of the dice.
Log in to reply
In fact, these other answers smack of "magical" thinking. What magical force do you imagine is linking the outcomes of these two dice? Hint: there isn't any.
You are 100% correct and this is a classic case of overthinking. Each one is individual trial process. They are treating it as a set. That is the basic flaw in the solution. One dice is a 4. There is another that has a 1 in 6 chance of being a 6. They are confusing a set with independent actions.
I agree, exactly ! First die is 4, therefore 1,2,3,5 and 6 have no chance on first die. 1 out of 6 chance of 6 on second die. Tunnel vision here, Don`t see any other way to look at it. Ken
It's always amusing to browse through the probability problems and see the comments from people who just refuse to believe that their intuitions could be wrong.
It's true, if I told you "I just rolled a 4. What is the probability that my next roll is a 6?" Then the answer would be 1/6. However, if I roll two dice and then tell you "at least one of my two rolls was a 4. What is the probability that the other was a 6?" It's a completely different question, and yes the two independent events have now been tied by information about them. Go ahead and write down all 36 equally likely possibilities for rolling 2 dice. See how many of them contain "at least one 4." It's 11. So if I tell you at least one roll was a 4, there are now only 11 equally likely possibilities to choose from. How many of those also contain a 6? 2. 2/11 is the correct answer. You could also conduct this experiment yourself with a couple of dice if you want to waste a day proving yourself wrong. Record the results every time "at least 1" of your 2 dice is a 4
Log in to reply
Came back to this question after having read about the Monty Hall problem (https://en.wikipedia.org/wiki/Monty Hall problem) OK, you've convinced me, I've to admit you're right and I was wrong in my comment below. Tricky!
But the problem sir, is that there aren't 11 likely possibilites for this problem. Let me explain: We have die A and die B: The die that we are told that is 4 for sure is either A or B equally likely.
-If the die A is the one we are told that is 4, then we have a 1/6 for the die B to be 6.
-If the die B is the one we are told that is 4, then we have a 1/6 for the die A to be 6.
The outcome (4,4) is repetead twice (one in each escenario) since it's the only outcome who can appear in both escenarios. We have 11 diferrent possibles outcomes, but (4,4) is twice as common, so we end up having a 2/12, [1/6] ends up being the solution.
"Note: You are not told which of the numbers rolled is a 4."
This is very confusing and misleading. Obviously, it's one of the die that when rolled that came up as 4. The question then is the probability of the OTHER die coming up with a 6. The one die that was rolled is done, finished - ancient history. The second die is now rolled totally independent of the first die. So it has to be 1/6.
One of my beefs is the way some questions are phrased. Is it intentionally misleading and confusing or is the writer EASL (English as a second language).
Log in to reply
By saying "The one die that was rolled is done, finished - ancient history. The second die is now rolled totally independent of the first die." you are solving for the problem "The first die came up as 4." However this isn't necessarily the case, as we only know one of the two dies came up as a 4 but not which one. This changes the answer because of the case where both dies came up as a 4 has the same chance of happening as all the other possibilities.
@L.E I agree with you on the independence. The outcome of the first dice does not effect the second dice as they are independent.
It doesn't matter which dice rolled is the 4. Every roll of a fair dice is a completely independent event and has the same odds every time, 1/6. BTW, "You are not told which of the numbers rolled is a 4" makes no sense.
Completely agree there is a one in 6 chance of either die landing on a number. That's as far as it goes.
Their argument dictates that once the four is chosen there are only 11 possibilities left but this is untrue because with the four chosen, there are only 6 numbers that the second die can cast. What if the question was another four. Would that be 1 in 11 ? No. 1 in 6
Agree with all who stated that the dice are independent.
Poorly worded problem.
The way I read the question, one of the dice was a four; what are the odds that the other die was a six. Well, the other die has an equal chance of being any of the numbers from one to six (assuming we are talking about six sided standard dice). Everything else is superfluous.
The answer 2/11 is utter nonsense. Once one die is cast as a four it is irrelevant what the odds attributed to that die would be as they are no longer in play and you did specify that the four was known and actually used a diagram of a die to show that.
I have to agree with all those saying this is a poorly worded problem.
The clause stating you are not told which of the die is the 4 is a red herring, as you have two dice and are given the value of one of them. It doesn't matter which of the two it is because you are then asked the probability of the OTHER die (singular) being a six. Which means you are being asked the probability of a single die throw which is always 1/6.
Edit:
For the solution to be right the problem should have said
You have two fair dice, A and B. One die (you don't know which) shows a 4. What is the probability that die B shows a 6?
But as written, it clearly asks for the result of a single die roll.
It's 1/6. You have a no time linked the probabilities together. Since they are separate throws then the probability remains at 1/6.
PA
Incorrect, it is worded "the other number" implying a separate die. The chances of any single number on a 6 sided die is 1/6.
So glad others responded. Once the outcome of either die is is known, it becomes irrelevant to the outcome of the other die. 1/6
I am so glad someone agrees the die are independent of each other. The question is ambiguous. I teach statistics and these are one of those questions that make me so upset.
Log in to reply
I feel bad for your students
I teach English and THIS is an example of a comment that upsets me. Learn your grammar.
Independent rolls, but even if not still only 1/6 because we know one die is a four and are asked the probability of the other being a six. The four die can never be six because it is given that it is 4.
The hand written sketch is wrong - it suggests that the are two possibilities - a 6 and a 4 or a 4 and a 6, but we already know that it is a four and something else so it is a 1 in 6 chance. Please change the answer because 2 in 11 is bollox!
Thanks to all those who agree the probability is 1/6. I had quickly decided that was right and was shocked to see it was "wrong". The two die are independent. Whatever happens to one has no bearing on what happens to the other. So the question becomes really; "What is the probability of a thrown dice showing a six after one throw?" 1/6.
You folks are over thinking this by and far.
One dice roll is a 4 - that is immutable. Can't be changed. Therefore the probability is only on one die because nothing is holding them together so to speak - nothing to link their probabilities. Not defined by the question at least. The second die could be any number 1 through 6. Hence, the probability is 1/6.
Perhaps you meant to phrase it that if two fair dice are rolled, what is the probability that the result is (4,6) given that a 4 is already showing on one dice?
This way the probability is on the set, rather than the one die.
You have given us the probability that the pair has the value 4 and 6. But that wasn't the question. The question was: given that one die has the value 4, what is the probability that the second die has the value 6? The wording of the question is always tricky in these probability questions.
Poorly worded question here. A common issue in conditional probability!
The answer is 1/6 with 67% probability (given the information in the question) and 2/11 with 33% probability (given that answer was made available ... so simple use of Bayes Theory suggests perhaps that is the question that they intended to ask!)
I suggest it's re-worded before the whole user base gets confused!
EDIT: The Monty Hall problem and Spencer McLeod eventually convinced me that my reasoning was wrong...
I think the proposed solution of 2/11 is wrong. If you know that one of the dice has shown 4, then you're simply left with the other die only, and 1 relevant possibility out of 6.
2/11 is the probability of rolling the two dice and obtaining 4 for one (either the first or the second) and 6 for the other. This is different than the case of knowing that one of the two rolled 4. @Pranjal Jain and @Karthik Venkata are calculating this case, not what the question asks. In particular, if we look at the table of all possible events, the question is telling you that you're either in the row 4, or in the column 4, but the space of events has already been restricted to one of the two, you shouldn't consider both (yes, despite the last note, because we're told one rolled 4).
EDIT:
OK. Let's assume the probability of "the other dice" showing a 6 is 2/11.
Then the probability for "the other dice" to show any other number chosen among {1, 2, 3, 4, 5} has no reason to be different to 2/11, 6 is no magical number and both dice are supposed to be fair.
The probability for "the other dice" to show any number between 1 and 6 is therefore 6 x 2/11 = 12/11.
We just proved that 12/11 = 1 :).
The dies are not independent when you specify that you do not know which of the two is a four. This is why the 1/6 answer is incorrect and Karthik's answer is so good. QM pulls this kind of stuff with identical particles all the time.
Log in to reply
Had the question asked for the probability of the SUM of the two dice being 10, (4+6 or 6+4) then the 2/11ths stands, but it doesn't, the dice are two physically exclusive entities. The answer has to be 1/6th.
Log in to reply
Those actually are the exact same question. The only way for the two die to sum to 10 in this scenario are for one of them to be a 4 (the first or second, you don't know which) and the other to be a 6.
Can you provide an example in QM? State vectors are additive but remain distinct if that's what you were thinking of. Just like to get your take on this. Thanks.
We don't know enough to solve this problem.
It's important to know how we have got to the point that it is revealed that one of the numbers rolled was a 4.
First example: Someone has decided to roll the dice again and again, until he got at least a 4. He then reveals "I have rolled 2 fairs dice and there is at least a 4".
The solution in this case is 1 1 2 , which is the official expected solution.
Second example: Someone has decided to roll the dice only once and to reveal one of them. It happens that he reveals a 4, but it could have been another number.
In this case, which seems more logical, the solution is 6 1 .
The biggest problem here is that we are told we have 2 fair dice. Yet the depiction does NOT show 2 fair dice! While the one on the left could be fair, the one on the right is definitely not. No legal die will have that configuration. If the die is not legal, it is not fair. FYI, the total on each opposite side must be seven, but ALSO on the sides with 1, 2 and 3 pips, the pips will always form a triangle when observed from the intersection of their edges.
I personally do not agree with 2/11 or 1/5 as the answer. In the original chart, one die must be four. We needn't know which one. If the first die is four, the probability of the second is 1/6 of being a six. If the second die is four, the first is 1/6. That's 2/12 or 1/6. Each die has a 1/6 chance of rolling six independent of ANY other factor. It's like saying that if you roll 3 sixes in a row, the chances are diminished for another six on the next roll. It's still 1/6. However, the chances of rolling 4 sixes in a row is a different story, and is always 1/6x1/6x1/6x1/6.
If there were 10 dice, and 9 are not sixes, there is still a 1/6 chance of the last die rolling six.
I answered the "expected" answer of 2/11, but there's a strong case to be made for 1/5 instead. After all, the problem says "one of the numbers rolled is a 4", not "at least one of the one of the numbers is a 4".
Let A=other dice shows 6 and B= one dice shows 4. Call dice D1 and D2 So P(A|B)= P(A^B)/P(B) But P(B)= P(D1=4UD2=4) and P(A^B)= P[(D1=4^D2=6)U(D1=6^D2=4)]. Now it's easy.
1S = a Six is rolled, S1 = a Six is rolled on Dice no.1, S2 = a Six is rolled on Dice no.2,
F = at least a Four is rolled, 1F = a Four is rolled, F1 = a Four is rolled on Dice no.1, F2 = a Four is rolled on Dice no.2
Prob. that AT LEAST one of the numbers rolled is four = P(F) = P(F1 ∪ F2) = P(F1) + P(F2) - P(F1 ∩ F2) = 1/6 + 1/6 - 1/36 = 11/36
Prob. that the numbers rolled are four and six = P(1F ∩ 1S) = P(F1 ∩ S2) + P(S1 ∩ F2) = 1/6 * 1/6 + 1/6 * 1/6 = 1/18
Prob. that the other number rolled is a six
= P(1S | F) = P (1S ∩ F) / P(F) = P (1S ∩ 1F) / P(F) = (1/18) / (11/36) = 2/11
This problem is ambiguous I think...
(A) if you just are told at least a 4 appears, then the answer is 2/11
(B) if you look at a dice and see a 4, then the answer is 1/6
I guessed right the problem means A but it seems B is also reasonable since the word "reveal".
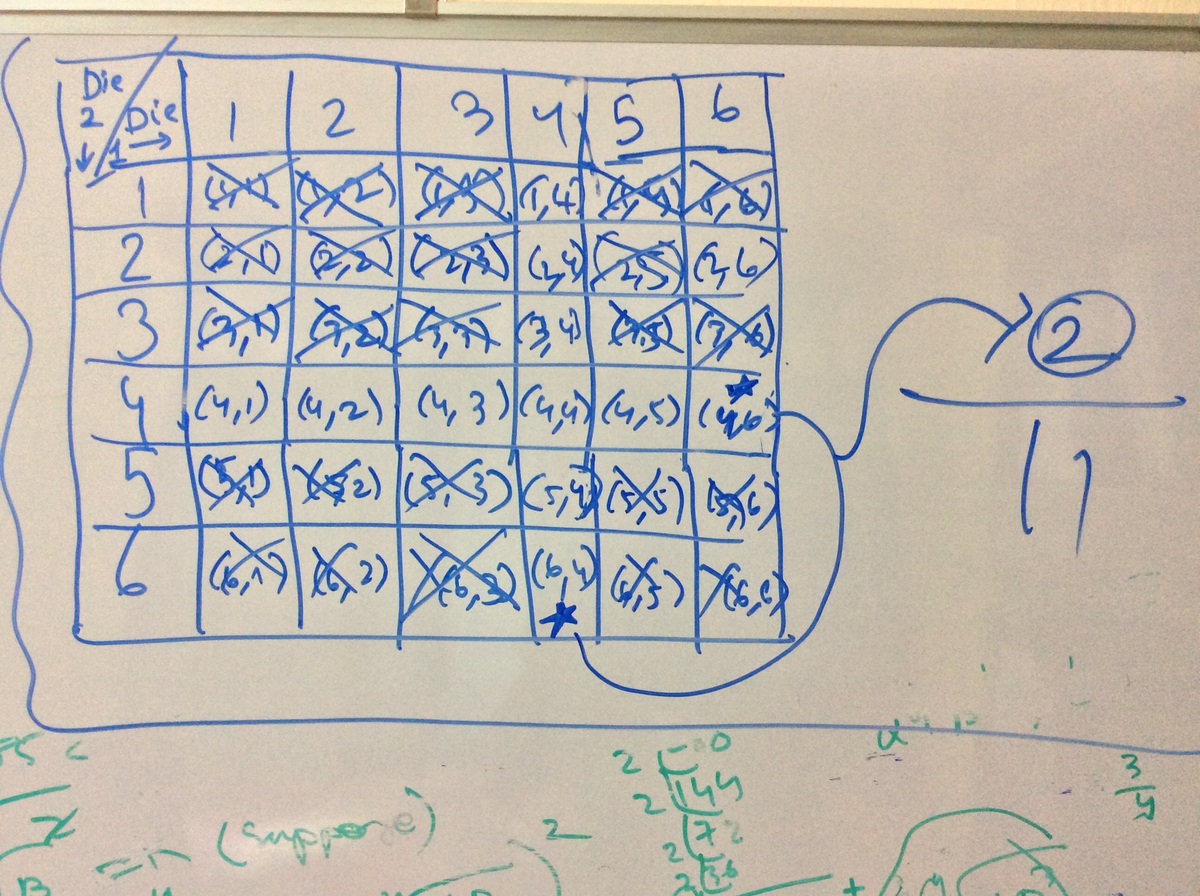
By listing out the equally likely outcomes
The yellow and tan squares indicate the total outcomes where it can be revealed that "one of the numbers is a 4".
The tan squares indicate the positive outcomes where "the other number rolled is a 6".
Hence, the probability is 2/11.
By conditional probability
A = Event of other dice showing 6
B = Event of one dice showing 4
P ( A ∣ B ) = P ( B ) P ( A ∩ B ) = 3 6 1 1 3 6 2 = 1 1 2 .