Did I Do Any Work?
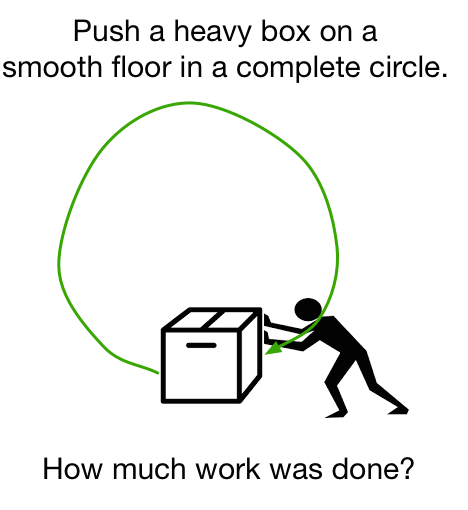
A heavy box was kept on a smooth floor, initially at rest. I started moving it in a circular path, and then brought it to rest when it completed one revolution.
How much work did I do on the box?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The problem that most people have is that they associate "work" with "expended energy" and/or "effort", both of which are strictly positive in the minds of most people. This is a problem with the English language. The amount of energy one must expend on a heavy box to accelerate it across a smooth floor, bring it to a halt, accelerate it back to its original position, and then bring it to rest is obviously positive. One would probably be quite tired from doing that. However, the mathematical definition of "work" says that there was no "work" done here, which may frustrate people (especially the one who moved the box!).
Log in to reply
Can someone tell me why the third option is incorrect ?
Log in to reply
Please have a look at the note at the end of the solution:
- Although the displacement of the box is zero, this does not imply that the work done is zero. If block started from rest, but it was moving with non-zero speed after one revolution, then the displacement of the box is zero, but work done is not.
But the angle between work and displacement is 0 so fdscos0 so +ve work is done right?
There is definitely work being done here. Work was done to set the box in motion, and was done to bring it back to rest. The NET work done is zero. Its still tiring because doing positive OR negative work on the block requires the fibers in your muscles to do positive work.
How's does this explanation make sense ? You applied a fixed amount of work and moved it a certain distance. So basically you did work. You are considering the final states of the object but how did you reach the final state?
Log in to reply
Hi Sandeep, the box is initially at rest, so I must apply some force to get it moving and I do some work. To stop the box, I must perform the same magnitude of work, but this time, it would be negative since my force is opposing the motion. They cancel each other, and the net work done is zero.
Log in to reply
So am I right in thinking if it had moved a distance but not in a circle work would have been done. Here, it's moved a distance which would suggest work done, but because for force has acted in one direction and then in the other (or at least its components have) this is why no work is done? Since it takes no resultant force to carry out the movement?
Log in to reply
@Tristan Allen – Please have a look at the note at the end of the solution:
-
Although the displacement of the box is zero, this does not imply that the work done is zero. If block started from rest, but it was moving with non-zero speed after one revolution, then the displacement of the box is zero, but work done is not.
-
Work done can be zero even if the displacement of the box is not zero. If the box moves in any arbitrary shape, even if its displacement is not zero, but its initial and final speeds are equal, then the work done is zero.
Here the conditions are totally different. When the box was at rest ,force is applied on the box . Since it travels circular path the direction of force must be changed and hence the box acquires tangential acceleration and also centripetal acceleration. Hence velocity of box also increases. On one complete rotation its velocity becomes maximum. Now inorder to keep it in rest , a large amount of force should be applied for some extra displacement in opposite direction.Hence some energy of the box remains for small time and then after covering more than initial position it will come to stop. Thus at the initial position change in kinetic energy is not zero.
Log in to reply
Hi Akash, could you please explain why "On one complete rotation its velocity becomes maximum"?
The problem statement mentions that the velocity of the box becomes zero (minimum) on one complete rotation. The box stops when it completes one revolution. It does not cover any extra distance.
Anyway, the final position of the box doesn't affect the work done by me. It doesn't matter if the box moved in a circle, square, or any other arbitrary shape. It doesn't matter if the final position of the box is the same as the initial position of the box. Only the difference in kinetic energy determines the work done by me. Since the box started from rest, and came back to rest, the change in its kinetic energy is zero, and therefore the work done by me is also zero.
Log in to reply
As the question says , the ball is at rest initially. So in order to move it we have to apply some force. But here we have to move the ball in circle so but obviously we have to change the direction of force at every moment.And also its direction should be tangential.Hence particle at every moment experience tangential as well as radial acceleration. As the question says after completing one revolution , it is stopped by applying opposing force. So during the revolution , the tangential force should be in same direction. So its tangential velocity will increase and so on one complete revolution it will be maximum.
Now, the reason for some extra displacement is :
when the box reached to its initial position, then at that instant it is stopped by applying a huge amount of force. So it will take some time to come in steady state. And for that much time It will cover some distance and so at initial position , box is in motion. So change in kinetic energy is not zero and hence work done is not zero.
isn't the third option correct as well? i mean that energy is a state function and since the final state of the box is the same as the initial state (meaning there was no net displacement), the work done on it is zero.
Log in to reply
The state that you are looking for is kinetic energy, and not displacement. Since the initial and the final kinetic energies are equal, the work done is zero.
-
Although the displacement of the box is zero, this does not imply that the work done is zero. If block started from rest, but it was moving with non-zero speed after one revolution, then the displacement of the box is zero, but work done is not.
-
Work done can be zero even if the displacement of the box is not zero. If the box moves in any arbitrary shape, even if its displacement is not zero, but its initial and final speeds are equal, then the work done is zero.
Although I got the answer wrong at the beginning, after thinking about it I agreed with Prasun's solution. Reason: Work is done on the box only if KE changes or PE changes. Since the box moved AGAINST ANY PREVIOUSLY EXISTING force, the PE did not change. So the parameter related to PE i.e. displacement becomes meaningless. (All this happens as there is no conservative force acting in the direction parallel to floor.) Now the only left option for work to change would be due to change in KE. (Acc. To Work-Energy theorem). Since KEi=KEf, the work done =O. MORAL: We should remember that we should consider the change in PE definition of work only if a conservative force is present in the desired direction! I hope my explanation is right. Please do correct me if I am wrong. 😇
Question. Since work equals force times displacement shouldn't answer 3 also be correct?
Log in to reply
Please have a look at the note at the end of the solution:
- Work done is not always equal to Force times displacement. It is true for only certain special cases. A better formula for work done is ∫ F ⋅ d s .
Ok, I think I understand that now, thank you! @Pranshu Gaba
Relevant wiki: Understanding the work-kinetic energy theorem
We can apply the work-kinetic energy theorem on the box. It states that the net work done on an object equals the change in kinetic energy. The only forces acting on the box are: gravitational force, the normal reaction by the floor, and the force applied by me on the box. Let W g , W N and W m e denote the work done by these forces respectively.
W g + W N + W m e = Δ KE
The gravitational force and the normal reaction are always perpendicular to the motion of the box, therefore they do not do any work on the box. Hence, W g , W N = 0 .
W m e = Δ KE
Since the initial and the final kinetic energy of the box is equal, Δ KE is zero, and work done by me is also zero. □
Note:
Work done is not always equal to Force times displacement. It is true for only certain special cases. A better formula for work done is ∫ F ⋅ d s .
Although the displacement of the box is zero, this does not imply that the work done is zero. If block started from rest, but it was moving with non-zero speed after one revolution, then the displacement of the box is zero, but work done is not.
Work done can be zero even if the displacement of the box is not zero. If the box moves in any arbitrary shape, even if its displacement is not zero, but its initial and final speeds are equal, then the work done is zero.