Differentiate how? PART 1
If x y = e x − y , then d x d y = _______________ .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I agree with this method and result, and I wonder why the "correct answer" has it in terms of log x and not ln x?
Log in to reply
log x can be assumed as a log with base 'e'
Log in to reply
I was under the assumption that log x is generally assumed to be log of x to the base of 10, maybe this is only applied to high school levels?
Log in to reply
@Wooil Jung – log x is generally assumed to be base 10, ln x is base e, and lg x is base 2
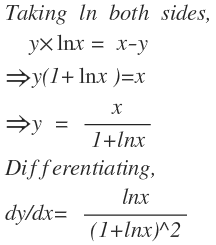
x y = e x − y = e y e x ⟹ ( e x ) y = e x , ∴ y ∗ l n ( e x ) = x , ⟹ y = l n ( e x ) x = 1 + l n x x d x d y = 1 + l n x 1 − ( 1 + l n x ) 2 x ∗ ( 0 + x 1 ) . . . . . . . . . . . . C h a i n R u l e . d x d y = ( 1 + l n x ) 2 l n x