Differentiation or inequality?
Given that x and y are positive real such that x + y = 1 , find the value of k such that the maximum value of x 4 y + x y 4 is k 1 .
The answer is 12.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Note that ⇒ is only used when a statement A implies a statement B , ie A ⇒ B . Never use it to mean equivalence.
We set x y = n as x y will be important afterwards. Factorize the original equation gives x y ( x 3 + y 3 ) , or, in another form x y ( ( x + y ) 3 − 3 x y ( x + y ) ) Now replace x y = n and x + y = 1 , which produce n ( 1 3 − 3 n ( 1 ) ) . To find the maximum of x 4 y + x y 4 , you will need to find n which produce the maximum number in n − 3 n 2 . Upon solving the equation, n which produce the maximum value is n = 6 1 and the equation produced maximum value of 1 2 1 , thus, k = 1 2
I'm writing x = 2 1 + h and y = 2 1 − h . Then x 4 y + x y 4 = x y ( x 3 + y 3 ) = − 3 h 4 + 2 1 h 2 + 1 6 1 = − 3 ( h 2 − 1 2 1 ) 2 + 1 2 1 , so that the maximum is 1 2 1 and k = 1 2
Nice solution but please explain how i will get the maximum of n − 3 n 2 ?
Log in to reply
You may use differentiation or inequality (as hinted in the title), but here I prefer doing in inequality and perfect square. − 3 n 2 + n = − 3 ( ( n 2 − 2 n ( 6 1 ) + ( 6 1 ) 2 ) − ( 6 1 ) 2 ) which equals to − 3 ( x − 6 1 ) 2 + 3 6 3 For all real number m , m 2 ≥ 0 , thus ( x − 6 1 ) 2 ≥ 0 − 3 ( x − 6 1 ) 2 ≤ 0 and finally − 3 ( x − 6 1 ) 2 + 3 6 3 ≤ 3 6 3 = 1 2 1
Log in to reply
Ok, but what should i do after differentiating − 6 n to find the maximum?
Log in to reply
@Priyanshu Mishra – You differentiate it to find the relative maximum (which happened to be the maximum point of the graph as well). Differentiating it gives 1 − 6 n = 0 (as at the extreme point, the slope is zero), or n = 6 1 . When you got n , just substitute into n − 3 n 2 , which provides 6 1 ( 1 − 3 ( 6 1 ) ) = 6 1 ( 1 − 6 3 ) = 6 1 × 2 1 = 1 2 1
Log in to reply
@Kay Xspre – Ok now i understood the whole solution.
Thanks a lot.
x 4 y + x y 4 ⇒ x 4 y + x y 4 = x y ( x 3 + y 3 ) = x y ( x + y ) ( x 2 + y 2 − x y ) x + y = 1 = x y ( [ x + y ] 2 − 2 x y − x y ) x 2 + y 2 = ( x + y ) 2 − 2 x y = x y ( 1 − 3 x y ) = − 3 ( x y ) 2 + x y = − 3 ( ( x y ) 2 − 3 1 x y + 3 6 1 − 3 6 1 ) = 1 2 1 − 3 ( x y − 6 1 ) 2 Since 3 ( x y − 6 1 ) 2 ≥ 0 ≤ 1 2 1 Note that x y − 6 1 = 0 , when x = 2 1 ± 6 3 , y = 2 1 ∓ 6 3
Well Gautam! That's the perfect method to solve.
Shouldn't it be (x^4)y+x(y^4) less than or equal to 1/12..
Log in to reply
You are right. A typo. I am amending the solution.
Need to do one more step to show that the system of equations x y = 1 / 6 , x + y = 1 has a real positive solution.
Log in to reply
You are right. I am amending the solution.
As both x and y are positive real numbers so
s i n 2 ( x ) + c o s 2 ( x ) = 1
Let x = s i n 2 ( x ) a n d y = c o s 2 ( x )
On putting values we get s i n 8 ( x ) c o s 2 ( x ) + c o s 8 ( x ) s i n 2 ( x )
s i n 2 ( x ) c o s 2 ( x ) { ( c o s 6 ( x ) + s i n 6 x ) }
Now as ( s i n 2 ( x ) + c o s 2 ( x ) ) 3 = 1
c o s 6 ( x ) + s i n 6 ( x ) = 1 − 3 s i n 2 ( x ) c o s 2 ( x )
Also s i n 2 ( x ) c o s 2 ( x ) = 4 1 s i n 2 ( 2 x )
Using these manipulations we get
1 6 − 3 s i n 4 ( 2 x ) + 4 1 s i n 2 ( 2 x )
This expression will attain it's maximum value when s i n 2 ( 2 x ) = 3 2 and this is in the range of values which s i n 2 ( 2 x ) can attain. So on putting values we get it's maximum value as 1 2 1 .
Stating that x = sin 2 x is not how one should make use of substitution. The equation x = sin 2 x is only true for some x ∈ [ 0 , 1 ] . It is better to let x = sin 2 t or x = sin 2 θ instead, for example.
Thanks for another solution :)
Let x=cos^2(m) and y=sin^2(m).
required expression =z-3*z^2 . Where z=xy. Hence max value of this parabola is 1/12.
let f= (x^4)y+ x(y^4). we can write f=xy[1 -3xy]. take xy=t. then f= t[1-3t]. for' f ' to be maximum differentiation of 'f' ' w.r.to 't' must be zero. it gives t=1/6. hence xy=1/6. also given x + y=1. solving we get x=1/2 + sqrt(3)/6. and y= 1/2 - sqrt(3)/6. these values of x and Y satisfies given equation. hence f is maximum for xy =1/6. so maximum value of f = 1/6[ 1 - 3*(1/6)]=1/6[ 1 - 1/2]= 1/12. so 1/k = 1/12, hence k= 12.
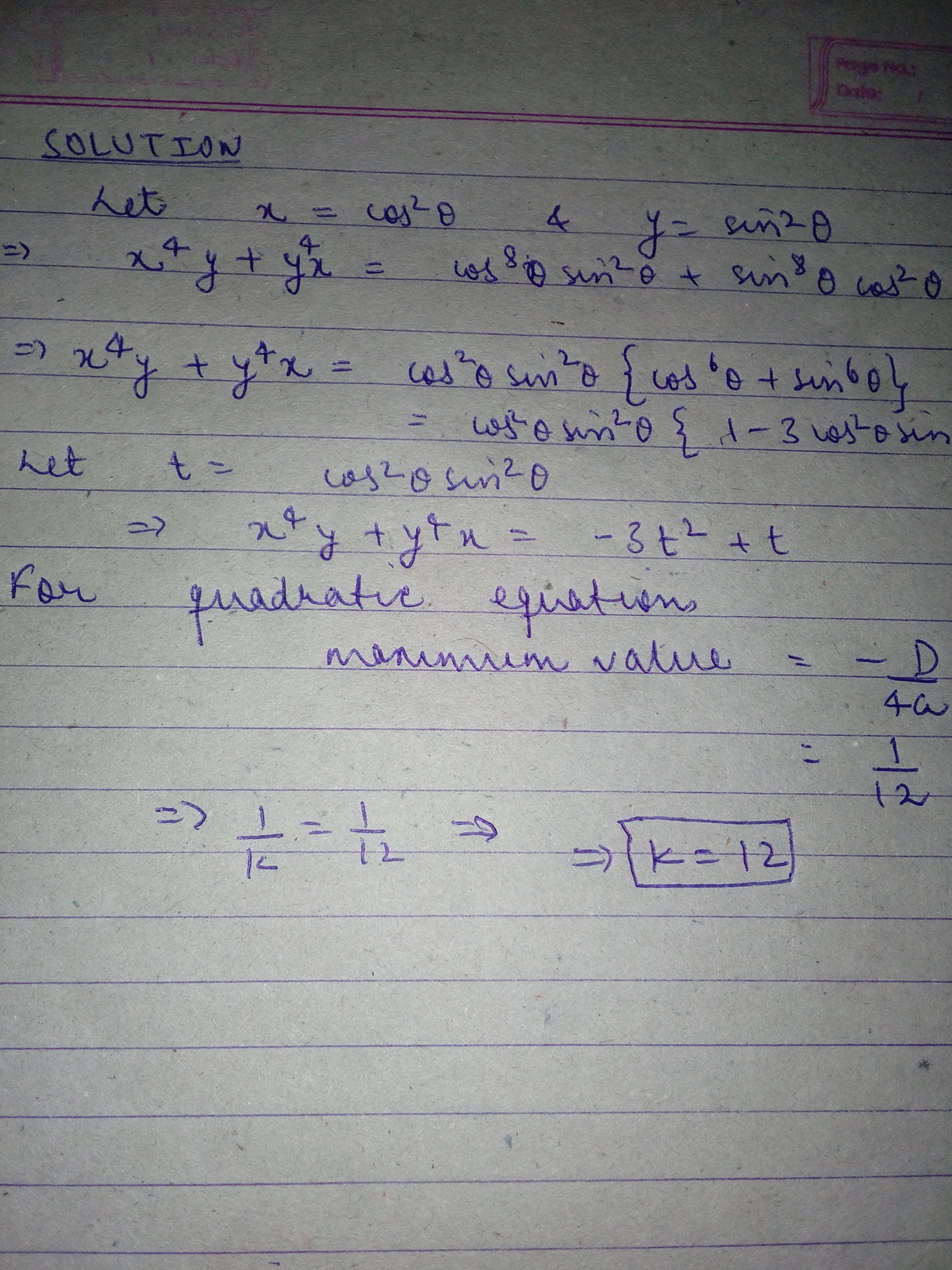
We factorize it as x y ( x 3 + y 3 ) ⇒ x y ( x 2 + y 2 − x y ) ⇒ x y ( 1 − 3 x y )
Now Applying AM-GM inequality.
2 3 x y + ( 1 − 3 x y ) ≥ 3 x y ( 1 − 3 x y )
Hence x y ( 1 − 3 x y ) ≤ 1 2 1