Dimples

In a spherical ball, a large number of dimples have been carved. The shape of these dimples is part of a sphere.
Is it possible for the dimpled ball to have a smaller surface area than it had before the dimples were carved?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
After carving, it should be stipulated that the before and after ball should have the same outside diameter. Otherwise, what's to keep me from carving it down to the same of a marble---with dimples?
Log in to reply
If you'd do that, it would hardly qualify as carving 'dimples'.
Log in to reply
Let us assume that the radius of original sphere (OS) is R. Therefore, SA (OS)=4πR^2 Now suppose we carve a dimple on the sphere (Since a picture of a golf ball is given and a dimple is given, according to psychological demand and appeal of question, each dimple will have a hemispherical shape)...Let radius of each hemispherical dimple(HD) be r Since R>>>r .°. SA of dimpled sphere is=4πR^2 + 2πr^2 - πr^2 Thus, SA of a dimpled sphere will always increase...irrespective if its a negligible quantity In response to the person who posted this question, Thus you are wrong. Since a dimple qualifies as a visible depression it will always increase the SA of the sphere
Log in to reply
@Eklavaya Singh – You have to subtract the surface area where you're putting the dimple in, then add the dimple curvature in. Looking at the question, they asked if it is possible to decrease SA. Yes! Is it possible to increase SA. Yes! You could do both! I consider a dimple as a new surface that is under the original surface. If you put a flat surface underneath, that will have less SA than the sphere. The person who made this was RIGHT! GOOD JOB, ARJEN!
Log in to reply
@Daniel Fisher – i did subtract the SA, and then added the CSA of the hemisphere
Log in to reply
@Eklavaya Singh – Then you added a piece with a larger curvature. If you do it that way, you can make the SA larger. I'm saying if the curvature is smaller, then you could decrease the curvature. The question only asked if it's possible to make the surface area smaller. It's possible to do both.
@Daniel Fisher – The question specifies that the dimples are sections of a sphere. Even if you are right about the flat bottom dimple, and since you ignore the walls of the cylinder you would create I am not convinced you are, the question does not allow that. "The shape of these dimples is part of a sphere."
Log in to reply
@Robert Balogh-Robinson – Even then, if the curvature is smaller (flatter) than the original surface, it's still a smaller surface area. Also, when someone claims that if the curvature is less, then the dimple is part of a larger sphere. HOWEVER, you must subtract parts of the larger sphere to fit the dimples onto the original spehere. I'm sorry if any of you got this wrong. The answer is still yes.
@Eklavaya Singh – The dimples on a golf ball are spherical, but certainly not half-spheres! Not only is that difficult to accomplish, but it would negatively impact the thermodynamics of the ball.
@Eklavaya Singh – It's wrong to assume that choosing a hemispherical shape of the dimples will give a general answer
@Eklavaya Singh – Exactly right! Is not the surface area of the dimple included?
@Eklavaya Singh – I agree with you
If one is a machinist, and is handed a steel ball, and uses a CNC mill to put in dimples, so that it looks like a golf ball, the machinist is going to find it a bit tricky not to end up undersizing the ball. Maybe I should post a geometry problem about that? Hmm...
Yeah, It would be carving caves !
I can't agree with.how can that be possible. explain me.
Log in to reply
I just did the math. It's not too complicated. Let's just say that the original sphere has a radius of 2.5 inches. If you cut a section of the sphere, which I call "section cap", with a radius of .2 inches, you will need to fill it with a dimple, which is the same as a section cap. The original SA of our sphere is 78.53981634 square inches. When we remove 1 section cap that is with a radius of .2 inch, the sphere's total SA will decrease by 0.125865414 square inches.
Not over yet! The hole needs to be filled with a new dimple. The new dimple has to have the same radius to fit in the hole. We can replace the original section cap with a new section cap from a larger sphere. Our larger sphere's radius is 3 inches. It's section cap with the same .2 inch radius would have an SA of 0.125803644 square inches. The new section cap (dimple) can fit in the same spot as the original section cap.
Since 0.125865414 square inches is greater than 0.125803644 square inches, the new total SA of our original sphere would be less after you add the new dimple SA to the original sphere's SA including the hole. If you're curious, the new SA is 78.53975457 square inches. 78.53975457 is smaller than 78.53981634. Just barely, but it is! That's just with one dimple. If you replace more original section caps with new section caps, the total SA will get even smaller.
The reverse is true if you use a new section cap from a sphere with a radius smaller than the original sphere.
Log in to reply
From the concept of surface tension we know every liquid wants to decrease it's surface area.as spherical shape has minimum area for a given volume so the shape of a drop is spherical. If dimple has less surface area than sphere so why the shape of a drop is not dimple shape?????
Log in to reply
@Emran Hossain – I'm not sure what you're asking. Sorry, but your English is a little weak for me to understand. But from my example, the dimples are small parts of spheres. If you take a part from a larger sphere, the SA will decrease. If you take a part from a smaller sphere, it will increase. I must have said that at least 4 times and no one seems to listen. The equations I used were provided by Arjen. I actually applied it and reached my results.
My calculations still agree with your statement about spheres having minimal surface area. You don't have to consider the sphere as a liquid.
Log in to reply
@Daniel Fisher – Emran asks a very good question... The answer is that the dimpled sphere also has a smaller volume than the smooth sphere. That is different from a liquid drop, which will attain the smallest area for the same volume.
If you were to make a "dimpled" water drop, you would have to compensate for the loss of volume by increasing the radius of the entire drop; this would cause the surface area to become bigger than before...
I'd like to have an actual formal proof or shown example, your little picture proves nothing. I've searched all over and have found nothing to support this reasoning. Sorry if I seem rude, but I hardly take anything at face value, especially when it comes to math. You also seem to disregard that you said a LARGE number of dimples. Just because one dimple can potentially reduce the surface area that means nothing if the surface is covered with these dimples.
Log in to reply
Here is a more formal approach.
Let R be the radius of the sphere, r the radius of a dimple, and r h o the radius of the circle C where the dimple intersects the sphere.
The part of the surface cut away by making the simple has the shape of a " spherical cap ". Its maximum height above the circle C is h 1 = R − R 2 − ρ 2 , and the area of the cap is A 1 = 2 π R h 1 = π ( ρ 2 + h 1 2 ) .
The area that is cut away is replaced by the inside surface of the dimple, which is also a spherical cap. h 2 = r − r 2 − ρ 2 , A 2 = 2 π r h 2 = π ( ρ 2 + h 2 2 ) . Thus carving the simple causes a change in the area of the sphere of Δ A = A 2 − A 1 = π ( ρ 2 + h 2 2 ) − π ( ρ 2 + h 1 2 ) = π ( h 2 2 − h 1 2 ) ; it is easy to see that Δ A < 0 if h 1 > h 2 and therefore R < r .
This proves the claim that "dimpling" the sphere lowers its surface area provided that the radius of curvature of the dimples is greater than that of the sphere.
In an extreme case, we can choose r → ∞ , which makes the "dimple" a flat circle of radius ρ . Then h 2 = 0 and Δ A = − π h 1 2 < 0 .
Log in to reply
Okay, there's been a lot of talk now about "reverse dimples" that result in net loss of surface area of a simple sphere. A flat spot is a kind of a "reverse dimple", only that the radius of curvature is infinite. Put in a single flat spot anywhere on the sphere, use a flat face grinder to create such a flat spot. The total surface area will then be less than before. Put in however many more flat spots one likes, which will further decrease the total surface area. Provided that the flat spot is created by using a grinding face that is wider than the original sphere, like how diamond cutters grind their stones to achieve...uh, brilliance.
At no time will grinding a new flat spot anywhere will increase the total surface area. This process can be continued until there's nothing left to grind.
Log in to reply
@Michael Mendrin – That is correct. I just did the math. It's not too complicated. Let's just say that the original sphere has a radius of 2.5 inches. If you cut a section of the sphere, which I call "section cap", with a radius of .2 inches, you will need to fill it with a dimple, which is the same as a section cap. The original SA of our sphere is 78.53981634 square inches. When we remove 1 section cap that is with a radius of .2 inch, the sphere's total SA will decrease by 0.125865414 square inches.
Not over yet! The hole needs to be filled with a new dimple. The new dimple has to have the same radius to fit in the hole. We can replace the original section cap with a new section cap from a larger sphere. Our larger sphere's radius is 3 inches. It's section cap with the same .2 inch radius would have an SA of 0.125803644 square inches. The new section cap (dimple) can fit in the same spot as the original section cap.
Since 0.125865414 square inches is greater than 0.125803644 square inches, the new total SA of our original sphere would be less after you add the new dimple SA to the original sphere's SA including the hole. If you're curious, the new SA is 78.53975457 square inches. 78.53975457 is smaller than 78.53981634. Just barely, but it is! That's just with one dimple. If you replace more original section caps with new section caps, the total SA will get even smaller.
The reverse is true if you use a new section cap from a sphere with a radius smaller than the original sphere.
Log in to reply
@Daniel Fisher – I tried it experimentally with a circle. The section cap from the larger sphere will have to have a smaller radius than 0.2"(considering your example) to fit in the smaller sphere. As Arjen later says that adding flatter dimples in the sphere reduces the volume, which is only possible if radius is reduced.
Log in to reply
@Mehdia Nadeem – That just further proves my example and Arjen's answer to this problem.
Log in to reply
@Daniel Fisher – I am a little confused, then why the following is written in your example " We can replace the original section cap with a new section cap from a larger sphere. Our larger sphere's radius is 3 inches. It's section cap with the same .2 inch radius would have an SA of 0.125803644 square inches. The new section cap (dimple) can fit in the same spot as the original section cap." If the new section cap has the same radius as the original section cap, it is not going to fit in the same spot from where the original section cap is removed.
Log in to reply
@Mehdia Nadeem – The hole in the original sphere has a radius of .2". That means there's an absence of material in that area. You fill that hole with something just as large as the hole (0.2" radius). It would fit PERFECTLY. If you used a smaller radius section cap, the section cap's surface area would be smaller, which still proves my point. Also, you would have a gap between the section cap and the original sphere if you used a smaller radius.
I guess we have a different definition of the section cap radius. Put the cap on any surface with the round side facing up. The bottom is the base. The radius comes from the base.
I don't understand why you're saying that if I remove something and replace it with something of the same size, it won't fit. That makes no sense. Just the shape of the object (curvature) changed.
Log in to reply
@Daniel Fisher – You are right, my definition of section cap radius was something else, my bad. Thanks for clearing it up though.
These are the equations that I used to help me reach my solution.
I think it would have been more interesting to require the volume to remain constant. I misunderstood that this was not part of the problem. The fact that a sphere has minimal surface area for a given volume is really the interesting part, don't you think? Do anything to the surface and you increase surface area if the volume must remain constant. Making large radius or flat "dimples" is not so interesting since you are also reducing the volume. Less volume leading to less surface is not surprising. Make one flat dimple and grind away everything. What's the big deal?
Log in to reply
The area-volume connection is certainly profound--
but what I like about this problem is that it addresses a misconception of how to apply that connection. The fact that 65% of people checks the wrong answer brings that out nicely.
So... I'd I had a sphere and carved one GIANT simple... That means I've created less surface area, that makes no sense. If I were to just create a HUGE single dimple despite the radius of dimple being larger, I have created waaaay more surface area. Your logic has come undone from a counterexample. I hope I don't have to provide a full proof/diagram. I'm literally saying you carve a giant dimple such that it essentially hollows out the sphere, but still retains much of the outer surface of the sphere. Not saying it's not possible, but I feel the argument given for your reasoning fails and is therefore incorrect.
Log in to reply
Your counterexample makes my point... and a picture really helps!
By making your big dimple, you
replace
the area shown in red by the area shown in green. This is clearly smaller!
Log in to reply
Of course, it is
possible
to increase the surface area. An extreme example is this:
However, the question was whether it was
possible
, rather than
necessary
for the new surface area to be less. Counterexamples cannot disprove it!
Log in to reply
@Arjen Vreugdenhil – Wait, people still commenting here LOL
BTW, great solution
Nice Question!
If you were to invert the dimple to make it a bump, that would increase the surface area, so wouldn't the same be true for the dimple?
Log in to reply
Good question... but if you reflect the dimple about a flat surface (the only way to preserve its area), the reflected dimple might have a smaller curvature than the ball itself. You would still be carving stuff away!
For all we know, the dimples could be totally flat (asuming an infinitely big sphere shape for the dimples). As long as the dimples have the shape of a LARGER sphere than the one being carved, the statement will be true. Same size gives same surface area, and smaller size gives a larger surface area.
If you mirror a small circular portion in surface it become a dimple in this way you can maintain the surface area just as previous. What if the dimple mirrored replaced with slightly bigger radius and it actually reduces the surface area and also curvature is preserved. This is my solution I got it right...!
Shaping the dimple with a section of the same diameter taken from any larger sphere will result in less surface area since the larger sphere's curve over the same circular sector will be flatter. As the the radius of the larger sphere approaches infinity the limiting (and minimum) case is the smaller sphere with flat dimples that are chord sections completely cut through when the dimple shape will no longer be part of the exterior shape of any sphere, even if every instance leading up to the limit does satisfy the problem statement.
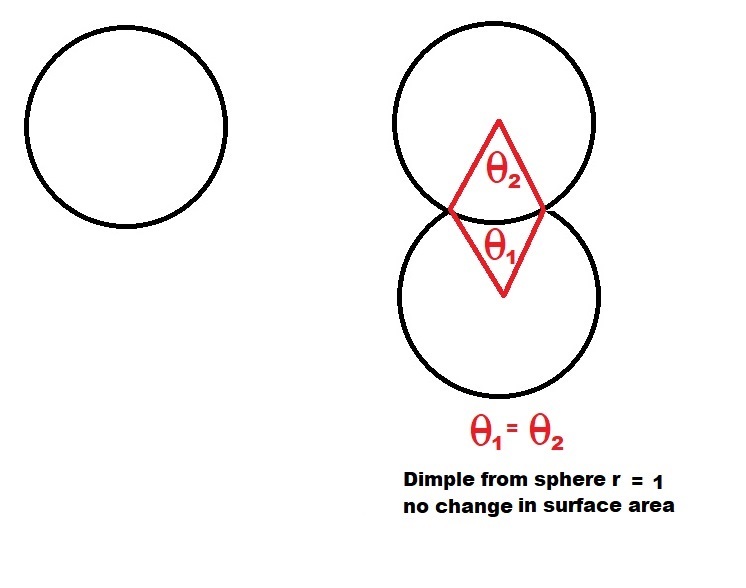
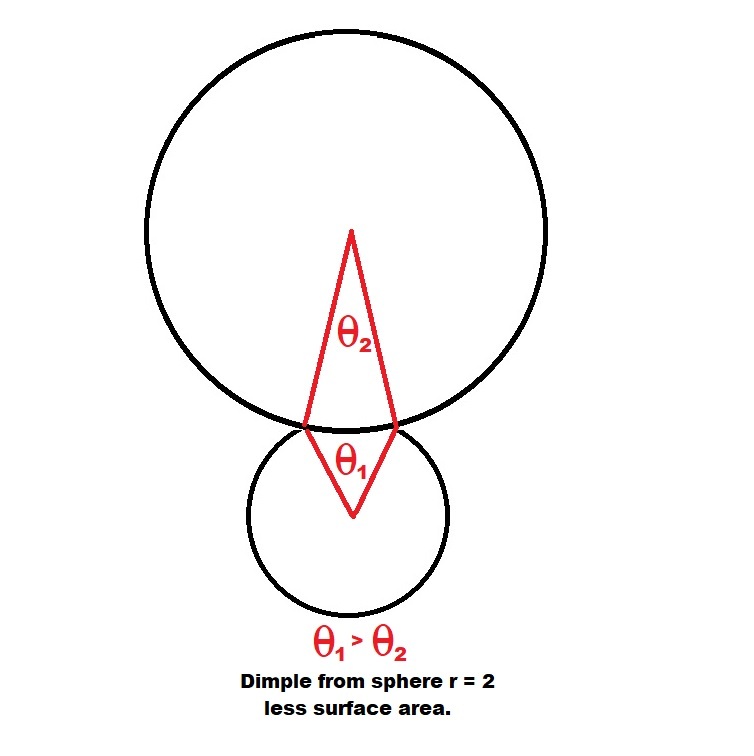
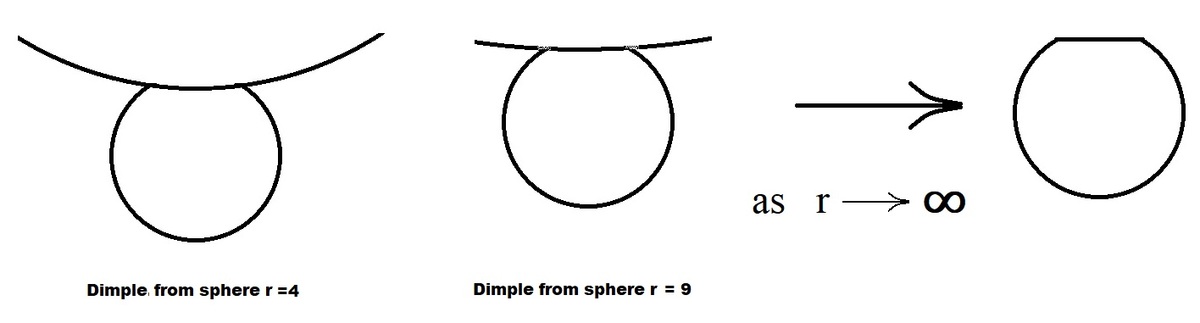
It just seems to me that the concave surface area created by dimpling would be less surface area as well as less overall mass.
The mass/volume will naturally be less. But if the curvature of the dimples is stronger than that of the ball (i.e. radius of curvature less than that of the ball), the area increases. It is therefore possible but not necessary for the surface area to decrease.
Compare flattening the sphere across the dimple circle, cutting the chord section completely (the shape of an "infiniite sphere", and the limit of all actual spheres as radius increases) against a dimple shaped like a sphere with the same radius as the circular edge of the dimple that goes in a deeply as possible, and a dimple shaped exactly like the sphere being dimpled.
I just imagined one huge dimple that cuts into pretty much all of the ball and leaves just a concave shell. For dimple diameter less than ball diameter, this object clearly has a lower surface area.
Depending on the size and number of the dimples , the radius is reduced to that extent inturn reducing the surface area. If the dimples are uniform , we can imazine them as 2 spheres with different surface areas
It is possible if the concave surface of the dimple has a larger radius of curvature than the convex surface of the ball.