Dipole and Ring Dynamics
This problem is based on a suggestion from Neeraj Anand Badgujar .
A particle with mass m = 1 and charge q = + 1 is confined to the ring x 2 + y 2 = 1 , where it can otherwise move freely. There is a charge q 1 = + 1 fixed at position ( x 1 , y 1 ) = ( 0 , 0 . 1 ) , and there is a charge q 2 = − 1 fixed at position ( x 2 , y 2 ) = ( 0 , − 0 . 1 ) . The particle on the ring is initially at rest at position ( x , y ) = ( cos ( π / 6 ) , sin ( π / 6 ) ) .
What is the time period of the particle's motion?
Details and Assumptions:
1)
Electric permittivity
ϵ
0
=
1
2)
There is no gravity
The answer is 68.48.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
@Karan Chatrath Can we solve it using Newton laws
Log in to reply
I see you edited this comment and deleted others. To answer your question, yes we can, but it would be much more tedious than what I have already done. While applying Newton's laws, you have to consider the reaction force between the particle and the ring. This introduces an additional variable in the problem. Using Lagrangian mechanics and energy conservation allows us to avoid this extra work.
Log in to reply
@Karan Chatrath
where did you use Lagrangian??? Did at that point conservation of( potential +k•E)
No matter how tedious it will be,I want to be done through Newton, tell me the concept I will do.
Log in to reply
@A Former Brilliant Member – In my previous comment I said 'Using Lagrangian mechanics and energy conservation allows us to avoid this extra work'. Instead of 'and', I should have typed 'or'. That was a typo. I did not use Lagrangian mechanics in this problem.
As for the Newtonian approach, I suggest you refer to the cone dynamics problem where I have shown how to approach a dynamics problem using the laws of motion.
Log in to reply
@Karan Chatrath – @Karan Chatrath can you give me link of any problem??
Log in to reply
@A Former Brilliant Member – https://brilliant.org/problems/cone-surface-dynamics/?ref_id=1588833
@A Former Brilliant Member – The concept remains the same. First, identify the forces acting on the particle. In this case, it is electrostatic force on the particle due to two fixed charges and a normal force on the particle due to the ring. Resolve each of these three forces along the X and Y directions and apply the second law of motion to obtain the acceleration along each direction. The accelerations you will get will be in terms of the normal force. Eliminate the normal force to obtain the final equation of motion. The expressions that you will work with are going to be very large.
@Karan Chatrath why did you integrate at last second step (L.H.S) from zero to 2 T p
Log in to reply
This is because the motion is periodic. The fact that motion is periodic is mentioned in the problem so I did not make the extra effort to prove that it is. In fact, proving that rigorously is difficult.
I mentioned in the solution that 'it is important to know that the particle moves from one extreme position to another in half a time period'. In periodic motion, a particle moves from its initial position back to its initial position in one time period. So it must move to from initial position to its other extreme position in half that time.
Log in to reply
@Karan Chatrath THANKS finally I understood your whole solution. Your solution is awesome and perfect
@Karan Chatrath agar apne part2 solve kar liya hai to. Please pehle sol. mai daluga Ok!
Log in to reply
@A Former Brilliant Member – Okay, I will share my solution after you do.
Log in to reply
@Karan Chatrath – @Karan Chatrath Bhaiya mera i m i n second order differential equation aarha 1 0 v − 1 + v ˙ = − 0 . 1 v ¨ iske solve karenge to v as a function of t aayega. Usko differntiate karenge time ke respect me, phir equal to 0.pgir vo jo time aayega usko vaapis put karenge.Bina kisi tool ke ye khud se nhi hoga i think.???
Log in to reply
@A Former Brilliant Member – The derivative of the velocity will have many roots. More than two, actually. You have to find all those roots and do a second derivative test to see which are local minima. Here too, you will find that many (more than 2) points fulfil the criterion for a local minimum. This work will be tedious.
@A Former Brilliant Member – Solve the differential equation and plot the graph of v ( t ) . Spot the minima using that graph. You can do it on Excel or over the internet by using this link:
https://www.desmos.com/calculator
Log in to reply
@Karan Chatrath – @Karan Chatrath ? Mujhe sirf 1 order aati hai bhaiya?
@Karan Chatrath Sir without graph how can we detect that range of θ is 6 − 7 π ≤ θ ≤ 6 π
Log in to reply
By using Rolle's theorem to show that there exist turning points in the graph, and also by computing the derivative of the P.E at the points θ = 6 π , θ = 6 5 π and θ = 6 − 7 π . Check the sign of the derivatives. At θ = 6 π the derivative will be positive and therefore the motion cannot exceed θ = 6 π as the PE cannot exceed its initial value. At θ = 6 − 7 π the derivative will be negative which means that PE will decrease as θ exceeds θ = 6 − 7 π
Plotting a graph is easier for me so I did it this way.
Log in to reply
@Karan Chatrath and how did you solve that last integral??
Log in to reply
@A Former Brilliant Member – Substituted all expressions and used Wolfram-Alpha for the rest.
Log in to reply
@Karan Chatrath – @Karan Chatrath Ok! BTW wolfram doesn't show solution of many integrals , how can we see solution of hard integrals??
Log in to reply
@A Former Brilliant Member – For single integrals:
https://www.integral-calculator.com/
Log in to reply
@Karan Chatrath – @Karan Chatrath Yeah its good. I like it. BTW double integrals??
Log in to reply
@A Former Brilliant Member – I don't know about any other online tool apart from Wolfram-Alpha.
The equilibrium position of the particle is at ( 0 , − 1 ) . The amplitude of motion is 3 2 π . So the particle will move between − 6 7 π and \dfrac{π}{6}. The problem with such problems is that they can't be solved analytically. Numerical technique is a must.
@Karan Chatrath
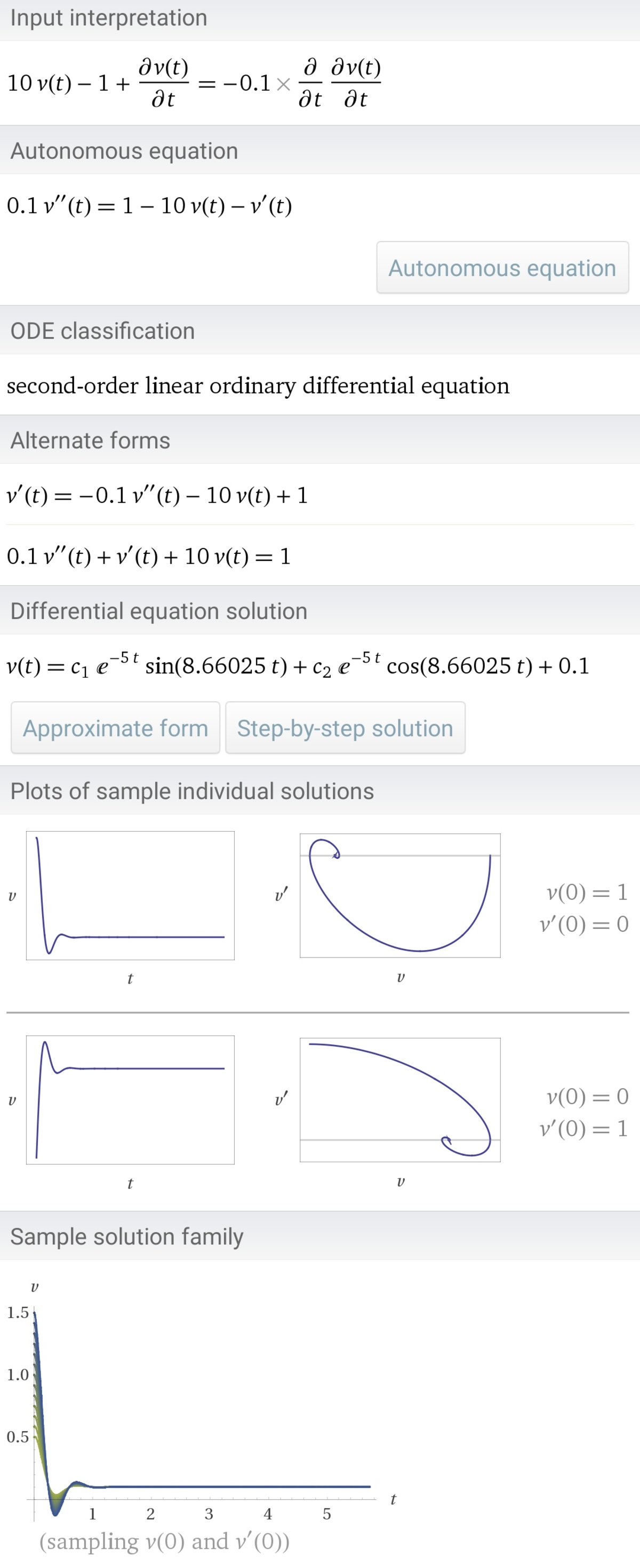
Using wolfram I am getting this but what does
c
1
and
c
2
mean????
Log in to reply
They are arbitrary constants. You can find them by substituting the initial conditions v ( 0 ) = ? and v ˙ ( 0 ) = ?
Log in to reply
@Karan Chatrath I am getting c 1 = − 0 . 1 c 2 = − 0 . 1 7 3 2
Log in to reply
@A Former Brilliant Member
–
@Karan Chatrath
after putting c1 and c2 I plotted this graph
Log in to reply
@A Former Brilliant Member – Check the 2nd order equation that you obtained. You might have made an algebraic error while deriving that.
Log in to reply
@Karan Chatrath – @Karan Chatrath now again after solving I am getting now 1 0 0 v − 1 0 + v ˙ + v ¨ = 0
Log in to reply
@A Former Brilliant Member – This is correct. I will not reply anymore.
@A Former Brilliant Member – @Karan Chatrath are these values correct c1 and c2??
Consider the particle to be at any arbitrary point on the ring. Its coordinates can be parameterised in polar coordinates as such:
x = cos θ y = sin θ
The potential energy of the particle due to the di-pole is:
V ( θ ) = 4 π 1 ⎝ ⎛ cos 2 θ + ( sin θ − 0 . 1 ) 2 1 − cos 2 θ + ( sin θ + 0 . 1 ) 2 1 ⎠ ⎞
The kinetic energy of the particle is:
T = 2 x ˙ 2 + y ˙ 2 = 2 θ ˙ 2
From this point, the problem can be easily solved using Lagrangian mechanics and numerical integration. However, I present a semi-analytical approach as follows.
In order to understand how the particle moves, it is important to first understand that since there are no dissipative forces acting on the system, energy is conserved. This means:
T + V ( θ ) = V i n i t + T i n i t
Here, the initial kinetic energy is zero as the particle is initially at rest and the initial potential energy can be found by substituting θ = π / 6 in the expression for the potential energy. This gives:
T + V ( θ ) = V i n i t
In the plot, θ ranges between 6 − 7 π ≤ θ ≤ 6 5 π . The black dashed line is V i n i t . The potential energy intersects the black line at three points just as mentioned earlier. The three points being θ = 6 π , θ = 6 5 π , and θ = 6 − 7 π .
It can be seen that in the interval 6 − 7 π ≤ θ ≤ 6 π , the particle's potential energy is lower than or equal to the initial potential energy. Therefore, the range θ is:
6 − 7 π ≤ θ ≤ 6 π
Now, having established the bounds of motion, it is important to know that the particle moves from one extreme position to another in half a time period. Using all this information and the energy conservation principle, we get:
T = V i n i t − V ( θ ) ⟹ 2 θ ˙ 2 = V i n i t − V ( θ ) ⟹ θ ˙ = − 2 ( V i n i t − V ( θ ) )
An extra negative sign is introduced as since time increases, θ decreases. Let the time period be T p Separating variables and integrating:
∫ 0 T p / 2 d t = − ∫ π / 6 − 7 π / 6 2 ( V i n i t − V ( θ ) ) d θ T p = 2 ∫ − 7 π / 6 π / 6 2 ( V i n i t − V ( θ ) ) d θ ≈ 6 8 . 4 8 0 7