Disc and Flux in a lane
A disc contains
1
C
charge and is uniformly distributed all over the disk surface and is placed at
x
=
0
,
y
2
+
z
2
≤
1
Find the electric flux passing through the surface
x
=
1
,
y
2
+
z
2
≤
1
I have provided the view of system from
−
Y
direction
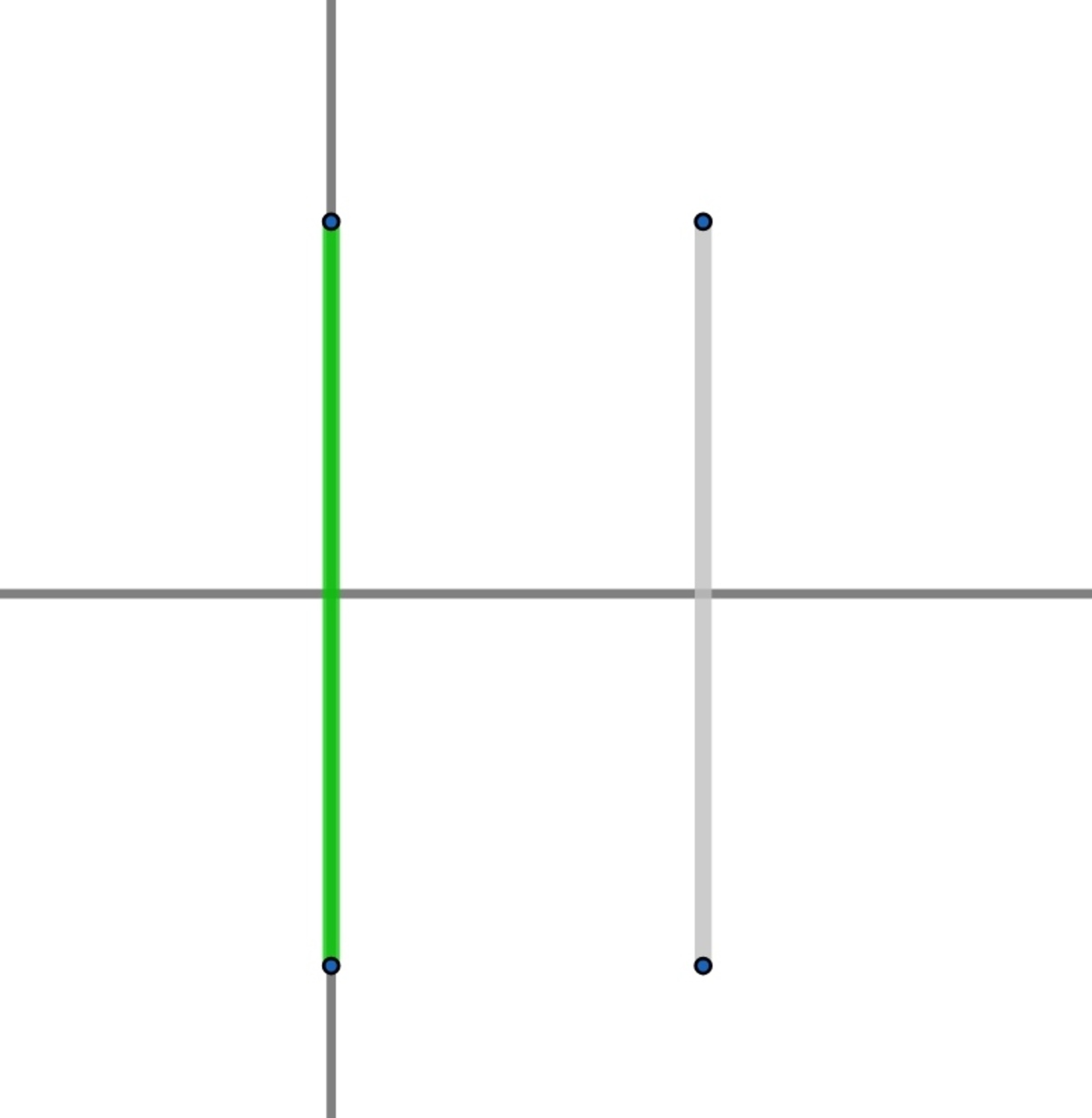 Inspiration
Details and Assumptions
1) Electric permittivity
ϵ
0
=
1
Inspiration
Details and Assumptions
1) Electric permittivity
ϵ
0
=
1
The answer is 0.116.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution. I have solved it with triple integration because if you take a circular elementary washer at ring by going a random distance x the electric field due to a particular ring in disc at that all point is same. That way leads to triple integration. . I have uploaded a new question on moment of inertia https://brilliant.org/problems/expected-moment-part-3/
Log in to reply
@Karan Chatrath
i have copied your code to brilliant coding environment and here the code is not running. Can you help me in identifying the mistake??
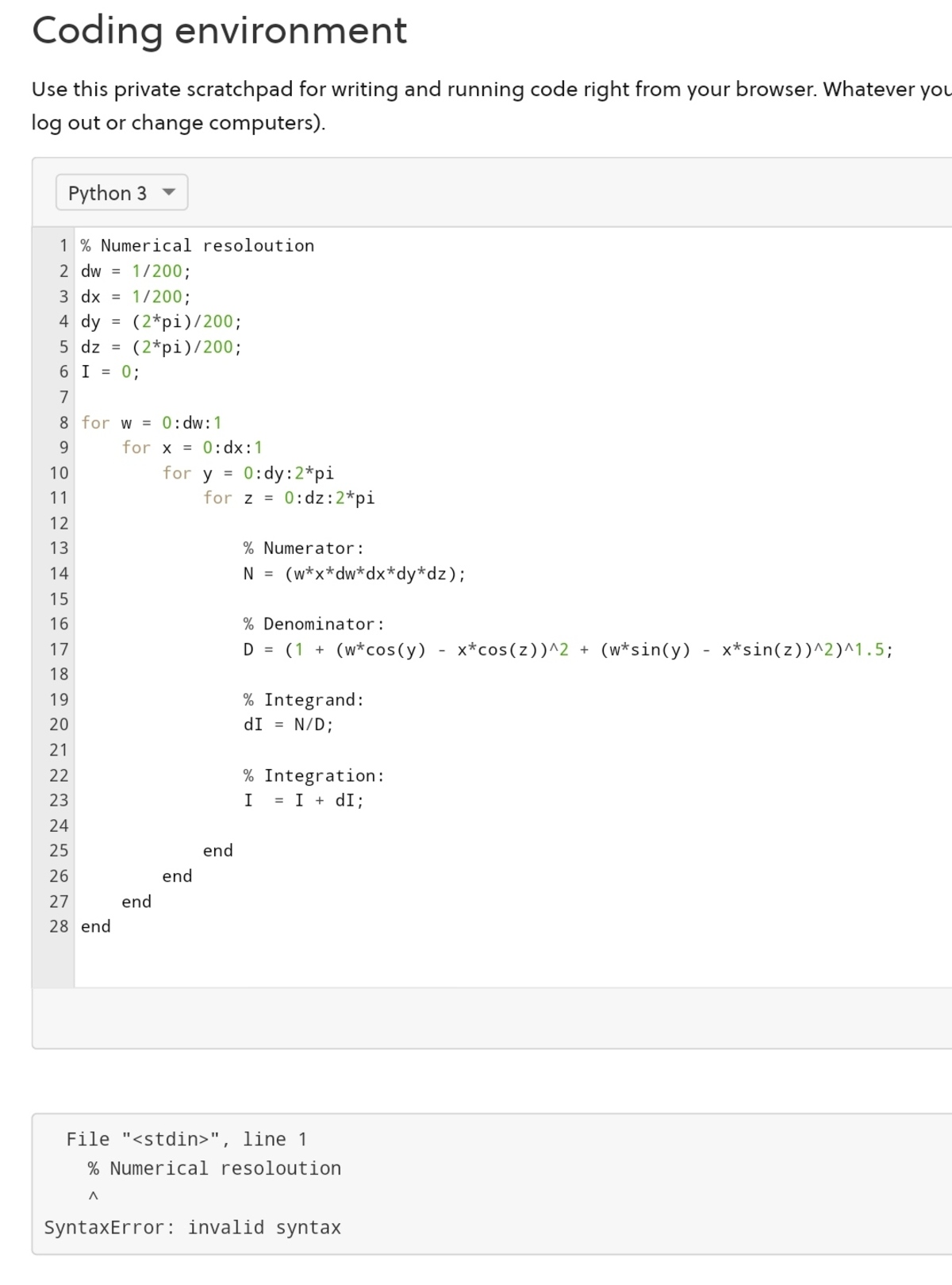
@Karan Chatrath Sir I was running this code in my laptop in sublime text editor version 3.2.2 . I copied you code and the code was not running. Can you please tell me where is the problem??
Log in to reply
The code is not typed in the Python language. In fact, my codes will not run in the Brilliant coding environment.
Nice problem. This one ends up being a quadruple integral. Given that these are disks, I recommend describing the surfaces as y 2 + z 2 ≤ 1
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 |
|
I observe different results. On taking N = 1 0 0 , I get ϕ ≈ 0 . 1 2 0 3 and on taking N = 2 0 0 , I get ϕ ≈ 0 . 1 1 8 2 . Given that a quadruple integral is to be solved, I find it strange that the results are so different from yours. Of-course the programming style is different but that shouldn't affect the numerics as the integration technique is similar to what you did. I will post my solution soon.
As for the problem statement, I would recommend that apart from the surface definitions, the phrasing of the charge distribution needs to be made clearer. It should be mentioned that 'the charge is uniformly distributed all over the disk surface'.
Log in to reply
Interesting. This one is difficult to do convergence testing on, because the problem scales as N 4 . It was fortunate that N = 1 0 0 and N = 2 0 0 gave similar results. I also thought about finding the flux through a cylindrical surface as well as an identical disk on the other end, to check against Gauss's Law (but didn't do so).
Log in to reply
Nice idea. But as you rightly say, computationally expensive. I have shared my solution. Please take a look and see if something catches your eye. Thanks in advance.
Log in to reply
@Karan Chatrath – I gave it a rough looking over, and the two solutions appear the same
@Steven Chase Sir I will post a question like this only and in that question the surface charge density in a disk is varying, and we have to calculate flux, like this only. I think it would be more interesting.
Log in to reply
@A Former Brilliant Member – Yeah, that sounds like a good one
Log in to reply
@Steven Chase – @Steven Chase I have uploaded a new follow up here https://brilliant.org/problems/expected-moment-part-3/
@Steven Chase Sir I am crying why you rotate the loop, it's centre normal vector in the direction 1 , 2 , 3 . I will not able to solve. I just want to ask can I solve that question with pen ,page and wolfram ??please.
@Karan Chatrath I have updated the question.
Consider a point on the charged surface:
r 1 = ( 0 , r 1 cos α , r 1 sin α )
Consider an elementary charge on that surface around this point which is:
d Q = π r 1 d r 1 d α
Consider a point on the second surface:
r 2 = ( 1 , r 2 cos β , r 2 sin β )
A surface area element on this surface is:
d S = r 2 d r 2 d β i ^
Electric field due to the elementary charge is:
d E = 4 π d Q ( ∣ r 2 − r 1 ∣ 3 r 2 − r 1 )
Elementary flux is:
d ϕ = d E ⋅ d S
This simplifies to:
d ϕ = 4 π 2 1 ⎝ ⎜ ⎛ ( 1 + ( r 2 cos β − r 1 cos α ) 2 + ( r 2 sin β − r 1 sin α ) 2 ) 1 . 5 r 1 r 2 d r 1 d α d r 2 d β ⎠ ⎟ ⎞
ϕ = 4 π 2 1 ∫ 0 1 ∫ 0 1 ∫ 0 2 π ∫ 0 2 π ( 1 + ( r 2 cos β − r 1 cos α ) 2 + ( r 2 sin β − r 1 sin α ) 2 ) 1 . 5 r 1 r 2 d r 1 d r 2 d α d β
Code attached below. Here, w = r 1 , x = r 2 , y = α , z = β .