Disc Partitioned - 1
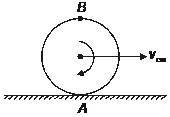
There is a circular disc of radius R which is undergoing pure rolling on a surface.
If V is the velocity of center of mass of the disc, then find the area of collection of points on the disc for which the magnitude of velocity is less than V in SI units.
Given R = 1 meter .
The answer is 1.228369.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Great question
nice one!!
Good ques bro Is it original ??
Log in to reply
Not really. Kinda modified though. It'll be a better question if I ask for the ratio of kinetic energies of the two parts. But I wasn't sure if people would be able to solve that much. I might make a part two!
Log in to reply
Yes I am waiting for that!!!!!!!!!
Log in to reply
@Gauri shankar Mishra – Try this now! Disc Partitioned - 2
Really enjoyed solving and looking for part 2
Log in to reply
Putting up part two. I think its crazy tough and messy too!
Log in to reply
where is it?
Log in to reply
@Aryan Goyat – Disc Partitioned - 2 There you go! Enjoy :D
Log in to reply
@Jatin Sharma – i wanted to know the ratio of the moment of inertia has to be found about cm in part 2 and if yes is the answer around 1.71 as it my last chance to answer it correctly, i will immediately delete the comment after your respond .
Log in to reply
@Aryan Goyat – Really sorry for the confusion there. Totally My bad! I have amended the question accordingly. And there is no need for you to delete the comment :) Its alright. And sorry for wasting your chances. I will post the question again deleting this one. So you can restart :). There is no other one who has attempted anyway.
Wow. Brilliant solution. I was thinking about the same question and posted it here. Thought it was original till I saw your question right now. Could you please check my question (https://brilliant.org/problems/geometry-or-rotation/?ref_id=1431938). I know its very similar, but if you want, I shall remove my question. Waiting for your reply. Thanks.
Log in to reply
Its alright! No need to remove it :) Glad to find someone with similar though process btw.
If we adopt a coordinate system O x y z with O x horizontal, O y vertically upwards, and O at the centre of the disc, then the angular velocity of the disc is ω = ⎝ ⎛ 0 0 − R V ⎠ ⎞ (since the disc is rolling, the point of contact A must be instantaneously at rest, and this determined the magnitude of the angular velocity). Thus the velocity of a point on the disc with coordinates ( x , y , 0 ) is v = ⎝ ⎛ V 0 0 ⎠ ⎞ + ω × ⎝ ⎛ x y 0 ⎠ ⎞ = ⎝ ⎛ V + R V y − R V x 0 ⎠ ⎞ and hence ∣ v ∣ < V precisely when x 2 + ( y + R ) 2 < R 2 . Thus the required region of the disc is the intersection of the two discs x 2 + y 2 < R 2 x 2 + ( y + R ) 2 < R 2 By standard circle-thinking, this region has area 2 [ 2 1 R 2 3 2 π − 2 1 R 2 sin 3 2 π ] = [ 3 2 π − 2 1 3 ] R 2 making the desired answer 3 2 π − 2 1 3 = 1 . 2 2 8 3 7 .
∣ v ∣ < ∣ V ∣
⇒ ∣ ω × r ∣ < ∣ ω × R ∣ Because V = ω × R where R is the position vector of COM of disc. As angle between ω and r (radius vector) is always 2 π , we can write it as : ∣ ω ∣ × ∣ r ∣ < ∣ ω ∣ × ∣ R ∣ ∵ s i n ( 2 π ) = 1
⇒ ∣ r ∣ < ∣ R ∣
Thus we can make an arc of radius R from the point of contact and the area of the disc inside that arc can easily be calculated by splitting it into two segments of equal area.
The final answer is 3 2 π − 2 3 square meters.