Disc Partitioned - 2
I suggest you check Disc Partitioned - 1 before you try this question.
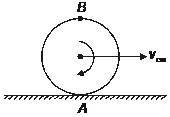
There is a circular disc of radius R which is undergoing pure rolling on a surface.
If V is the velocity of center of mass of the disc, let a part of the disc be the collection of points on the disc for which the magnitude of velocity is less than V in SI units.
Thus the disc is now partitioned. That is divided into two parts.
Find the ratio of the kinetic energies of the two parts of the disc.
The ratio must be greater than 1 i.e. the ratio of the more energetic part to the lesser one is required.
You may use a calculator in the end for the decimal answer.
The answer is 7.14094104.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice. Pretty lengthy wasn't it? Just a small suggestion. If you find the KE of the small one you can subtract it from the total KE to find the energy of the other part. Need not put the limits again. :)
Log in to reply
YEAH the solution was lengthy and for that very reason I didn't type it out. But I loved the hidden complexity of the Question. Hope you keep on posting such questions. And the limits thing I wrote was just to make it look more fancy ;P
Great solution
oh i got it but a REAL LENGTHY ONE.
-
you just need to find the ratio of moment of inertia of two parts about IAR ie instantaneous axis of rotation in this case the bottom most point.
-
just found the moment of inertia of lower most part and for the inertia of uppermost subtract it from total.
-
to find the the moment of inertia of the lower most part ,i found the moment of inertia of minor segments most challenging,i found moment of inertia about the center of circle,found the cm of the the segment and then finally found it about the bottom most point.
Kudos! Congrats! And I know right(its lengthy!)? The integration ticks you off! Tell me how you did it.. lets share methods.
Log in to reply
really enjoyed it looking for part 3
Log in to reply
I don't really have any ideas for part 3 xD
Log in to reply
@Jatin Sharma – u could try innovative problems in mechanics for ideas :)
Log in to reply
@Rohith M.Athreya – I already did one of them :). The last one seems lengthy even to read. But i'll get to it!
Log in to reply
@Jatin Sharma – yeah!! all the best
i will add as and when i get ideas
let me know when u post a good one :)
But i do have a slightly better solution. You can find the moment of inertia about IAR directly. Need not find the cm of segment! (i actually tried your way earlier but dropped it when i found i'll have to find com of segment!! Phew) Take the differential elements as arc drawn taking IAR as centre. Integral is a bit lengthy but surely lesser than what you must have done!
This isn't a solution but if you have attempted this question. Please share your line of thought and method!
well it was just ratio of moment of inertias. if u find moment of inertia of one part it suffices. of course about iaor as rotational kinetic energy alone can be considered at this point but was quite cumbersome to do the integration
Log in to reply
It really was. What did you take as your differential element?
Log in to reply
arc of a circle with differential angular displacement about IAOR
Log in to reply
@Rohith M.Athreya – Same here!
Log in to reply
@Jatin Sharma – but nice question
hadnt done any question along such lines before:)
looks u still didnt get collision after-effects
I could solve the first part because you had told it to me during our practicals :P This one was just calculus.
Great questions btw!
Since no one has done a LaTeX solution yet, I thought I would write one up!
First, we need to determine the section of the disc that has velocity less than V .
We note that since the disc is rolling without slipping, each point on the disc would be moving with velocity V , if the disc was not rotating. In addition, we know that with spinning, the angular velocity, ω is given by ω = R V .
Let θ be the angle between the vertical and the line extending from the centre to some point ( r , θ ) of the circle. For such a point, the translational velocity from rotation is given by ω r , so we break it into components, which gives us a general velocity vector:
v ( r , θ ) = ( V 0 ) + ( − ω r cos θ ω r sin θ ) = ( V − ω r cos θ ω r sin θ ) = V ( 1 − R r cos θ R r sin θ )
We can then conclude that the magnitude of velocity at the point ( r , θ ) is the norm of this vector:
v ( r , θ ) = v x 2 + v y 2 = V ( 1 − R r cos θ ) 2 + ( R r sin θ ) 2 = V 1 + R 2 r 2 − R 2 r cos θ
We are interested in points ( r , θ ) such that v ( r , θ ) < V :
V 1 + R 2 r 2 − R 2 r cos θ < V ⇒ 1 + R 2 r 2 − R 2 r cos θ < 1 ⇒ R 2 r 2 − R 2 r cos θ < 0 ⇒ 0 ≤ r < 2 R cos θ
Clearly, it must also be true that 0 ≤ r ≤ R . We know that cos ( π / 3 ) = cos ( 5 π / 3 ) = 1 / 2 , so it follows that for angles ranging from 0 to π / 3 and from 5 π / 3 to 2 π , all of the points on the disc will travel with velocity less than V .
We also note that cos ( π / 2 ) = cos ( 3 π / 2 ) = 0 , so from θ = π / 3 to θ = π / 2 and from θ = 3 π / 2 to θ = 5 π / 3 , the range of possible values of r is given by 0 < r < 2 R cos θ . This allows us to integrate across each infinitesimal contribution to the kinetic energy in these bounds. We must calculate two integrals, with each set of bounds. Note that we use the symmetry of the problem to simplify the integrals:
K 0 = 2 ∫ 0 π / 3 ∫ 0 R 2 1 v ( r , θ ) 2 d m = ∫ 0 π / 3 ∫ 0 R v ( r , θ ) 2 A M r d r d θ = π R 2 M V 2 ∫ 0 π / 3 ∫ 0 R r + R 2 r 3 − R 2 r 2 cos θ d r d θ
= π M V 2 ∫ 0 π / 3 4 3 − 3 2 cos θ d θ
We set up the second integral in a similar fashion, but using the second set of bounds:
K 1 = π R 2 M V 2 ∫ π / 3 π / 2 ∫ 0 2 R cos θ r + R 2 r 3 − R 2 r 2 cos θ d r d θ = π M V 2 ∫ π / 3 π / 2 2 cos 2 θ − 3 4 cos 4 θ d θ
where we used the symmetry of the problem to simplify the integrals. We wish to find the total kinetic energy, K = K 0 + K 1 , so we have:
K = π M V 2 [ ∫ 0 π / 3 4 3 − 3 2 cos θ d θ + ∫ π / 3 π / 2 2 cos 2 θ − 3 4 cos 4 θ d θ ] ≈ π 0 . 2 8 9 4 M V 2
where we evaluated the final integral numerically. Finally, we note that the total kinetic energy of the rotating disc is given by the rotational kinetic energy, plus the translational kinetic energy:
K tot = 2 1 M V 2 + 2 1 I ω 2 = 2 1 M V 2 + 4 1 M V 2 = 4 3 M V 2
so the kinetic energy of the other pat of the disc, K ′ is equal to K tot − K . This allows us to find the final ratio between the kinetic energies of the components of the disc:
R = K K tot − K = K K tot − 1 = π 0 . 2 8 9 4 M V 2 4 3 M V 2 − 1 = ( 4 ) ( 0 . 2 8 9 4 ) 3 π − 1 ≈ 7 . 1 4
I would like to provide a solution to this fantastic question !!! PLEASE UPVOTE if you like it !!

