Disc Rotated Flatly?
A flat disc on the top of a rough, horizontal table with coefficient of friction μ is being rotated with angular velocity ω o .
How long will the disc rotate (in seconds) before coming to rest?
First, generalize, and then plug in the following values for the answer: ω o = 1 0 radian/s , R = 4 m , μ = 0 . 3 , g = 1 0 m/s 2 , M = 4 kg .
The answer is 10.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
great solution!!!!!
Log in to reply
:) Thanks. Then can you upvote?
Log in to reply
yes sure!!!
Log in to reply
@A Former Brilliant Member – Its original. I made it :) . How was the question?
Log in to reply
@Md Zuhair – Unfortunately, it already exists. [https://www.physicsgalaxy.com/lectures/1/1/44/239/Solved-Example-6]
Log in to reply
@Swapnil Das – :( I didnt knew.
Log in to reply
@Md Zuhair – Actually its a common problem .( its in irodov as well)
@Md Zuhair – great ..... i had previouly done a "rod" and "cone" version of it.
Log in to reply
@A Former Brilliant Member – Here in brilliant? Can you please share the links. I'd love to do those!
Log in to reply
@Md Zuhair – https://brilliant.org/problems/variable-friction-on-horizontal-rod/
@Md Zuhair – https://brilliant.org/problems/a-small-trick/?ref_id=1404304
@Md Zuhair – https://brilliant.org/problems/variable-friction-on-the-horizontal-disc/?group=ksfPlKRpzV87&ref_id=475764
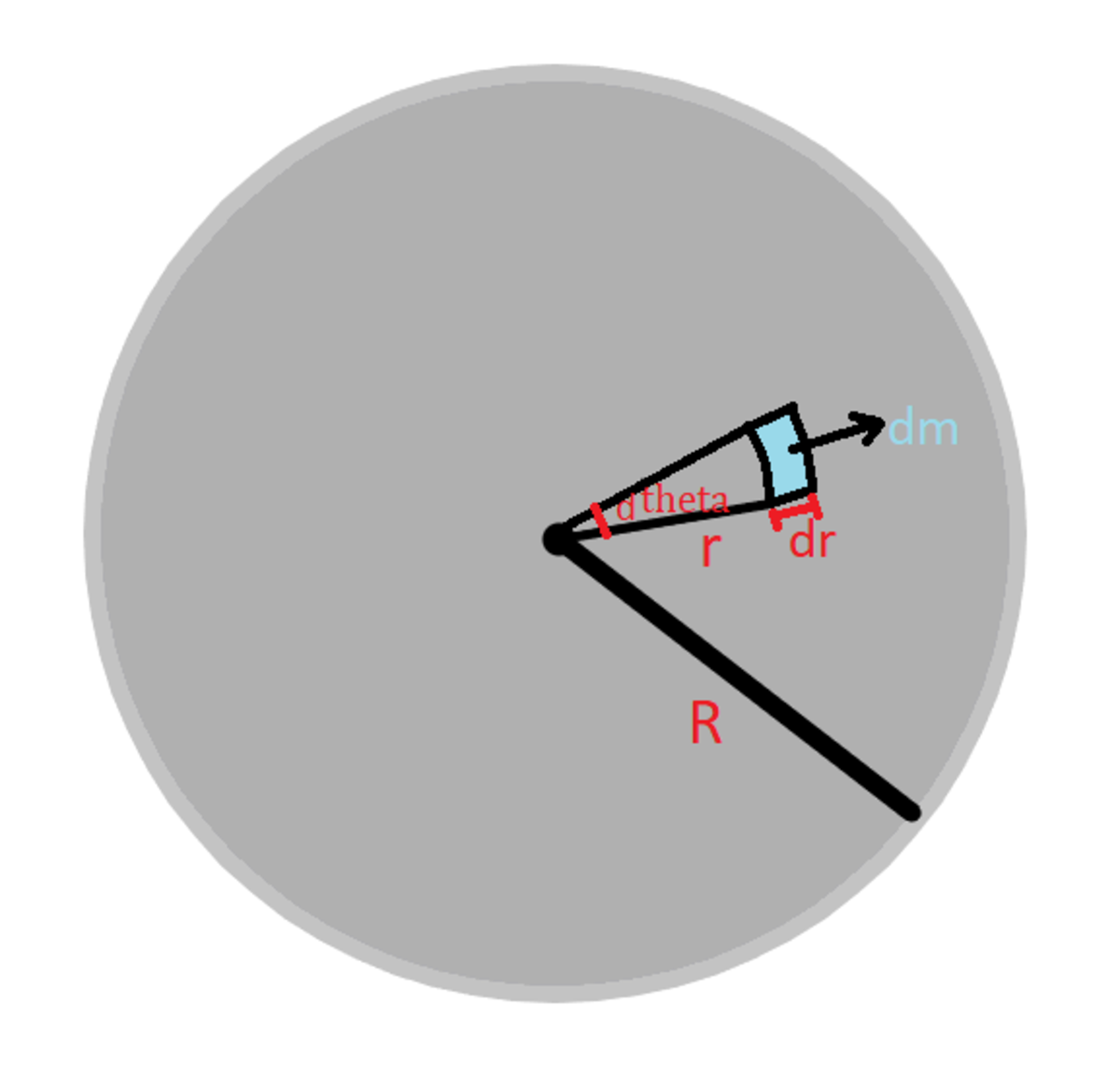 Mass element(dm)
Mass element(dm)
Assuming uniform mass distribution,
π R 2 M = r d θ d r d m ⇒ d m = π R 2 M r d θ d r
Now, since d τ = μ d m g r = π R 2 μ M g r 2 d θ d r ,
∴ τ = ∫ d τ = ∫ 0 2 π d θ ∫ 0 R π R 2 μ M g r 2 d r = R 2 2 μ M g ( 3 R 3 ) = 3 2 μ M g R
Using τ = I α
α = I d i s c τ = 3 R 4 μ g
as I d i s c = 2 M R 2 . Finally,
ω 0 = 3 R 4 μ g t ⇒ t = 4 μ g 3 ω 0 R
Evaluating at the given values, we get t = 1 0 s. As you can see, stoppage time is independent of mass.
Lets take an elemental part at distance x from center whose width is d x .
So Mass of elemental part d m = π R 2 M 2 π x d x
So d N = d m g
⟹ d N = π R 2 M g 2 π x d x [Normal reaction of the element]
d F = π R 2 M g μ 2 π x d x [Friction on the element]
Then Torque due to friction which stops it is
d F . x = π R 2 M g μ 2 π x 2 d x
⟹ d τ = π R 2 M g μ 2 π x 2 d x
Integrating from 0 → R we get
⟹ ∫ 0 τ d τ = ∫ 0 R π R 2 M g μ 2 π x 2 d x
τ = 3 R 2 2 M g μ R 3
τ = 3 2 M g μ R
I α = 3 2 M g μ R
α = 3 I 2 M g μ R
Now by equation of rotation we know
0 = ω o − α t
α ω o = t
⟹ 3 I 2 M g μ R ω o = t
Now for disc, I = 2 1 M R 2
Putting it we get
⟹ 4 g μ 3 ω o R = t
⟹ t = 4 g μ 3 ω o R
Putting values we get
t = 1 0 s