Displacement Dilemma
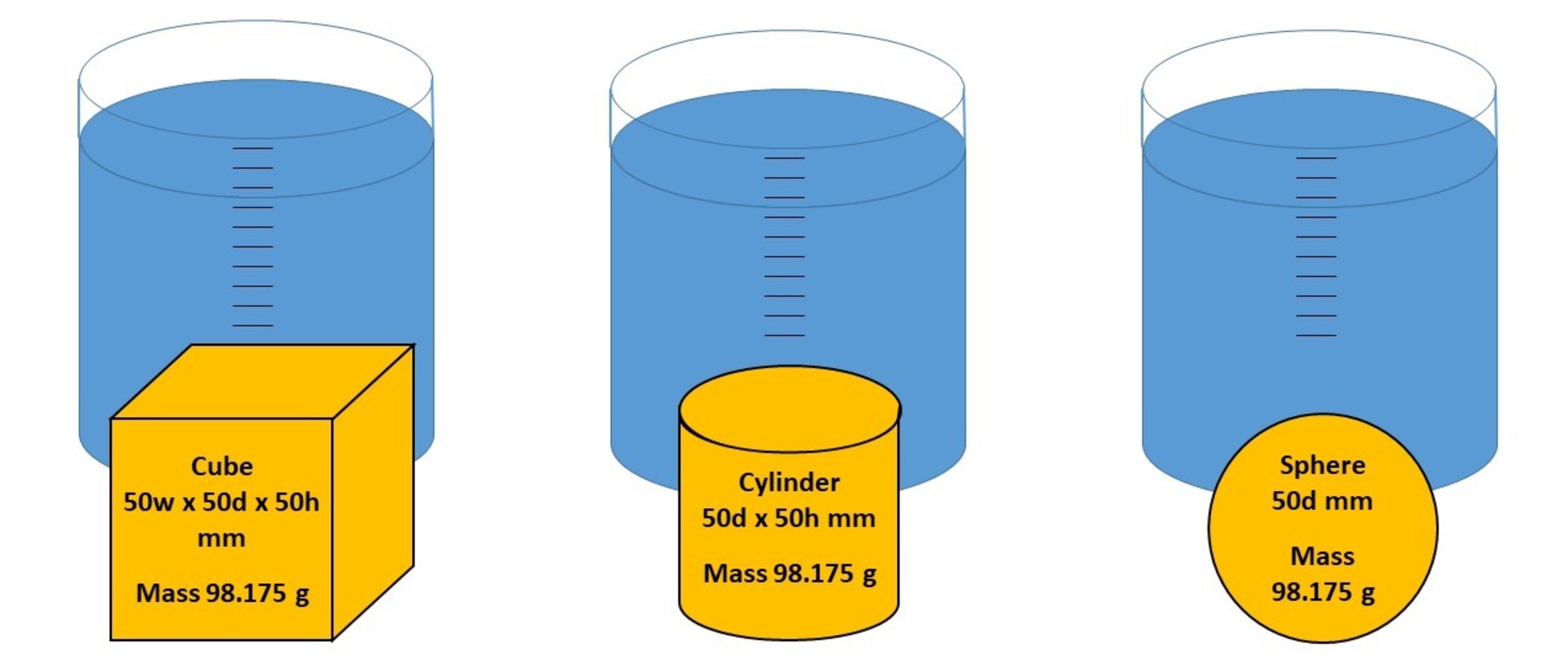
Given 3 identical containers with equal amounts of water in each and three geometric shapes as follows:
- Cube measuring 50 mm wide by 50 mm deep by 50 mm high
- Cylinder measuring 50 mm diameter by 50 mm high
- Sphere measuring 50 mm diameter
with all three shapes weighing 98.175 grams each.
Which shape will displace the greatest volume of water when placed in one of the containers?
Assumptions:
- One milliliter (1 ml) of water equals one gram (1 g).
- Volumes are rounded to 3 places after the decimal.
- There is no significant effect from air or water pressure, temperature, or surface tension.
- The shapes do not absorb water.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
BONUS QUESTION: How would your answer change if the container held a liquid that had a density of 1.5 grams per milliliter or .75 grams per milliliter?
Simple Explanation It can be observed that the sphere will fit inside the cylinder and the cylinder will fit inside the cube, both with space not occupied, therefore the cube has the most total volume and the sphere has the least.
The key is what happens when they are placed in the water as the cube floats, the cylinder has neutral buoyancy, and the sphere sinks. Because of this, the sphere displaces its entire volume (65.450 ml), the cylinder displaces its entire volume (98.175 ml) which equals its weight (98.175 g), and the cube displaces only that portion of its volume that is under water due to it's weight (98.175 ml), therefore the cube and cylinder displace the same amount and more than the sphere.
Detailed Explaination First calculate the volume of each shape as follows:
Next, determine if the shape will sink or float by subtracting the weight of the water the shape would displace (if submerged) from the weight (mass) of the shapes.
Therefore: the cube and the cylinder each displace 98.175 ml of water, more than the 65.450 ml that the sphere displaces.