∣ x ∣ , Hoplessly Positive.
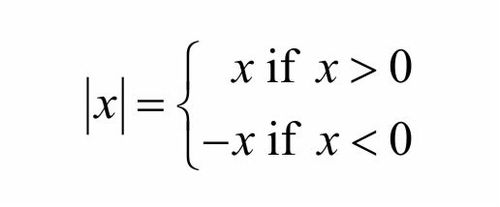 If
∣
x
∣
2
+
∣
x
∣
−
6
=
0
,
If
∣
x
∣
2
+
∣
x
∣
−
6
=
0
,
then which of the fowling option is true?
-
(A) Product of roots is − 6
-
(B) Sum of the roots is + 1 or − 1
-
(C) Both (A) and (B)
-
(D) None of these.
AYWC?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Well actually there are also infinitely many complex roots, e.g. x = ± 2 i , x = ( 1 ± i ) 2 , etc.
Edit: the general solution is − 2 ≤ Re ( x ) ≤ 2 , Im ( x ) = ± 4 − ( Re ( x ) ) 2 It is a circle of radius 2 centered about the origin in the complex plane. So the product is divergent and the sum is 0 .
or just observing the coefficents
Log in to reply
Sorry, what?
Log in to reply
vieta formula
Log in to reply
@Mardokay Mosazghi – hmm...we are having extraneous roots, will vieta work?
Log in to reply
@Soumo Mukherjee – i agree i guess it was just an observation btw nice solution sir
Log in to reply
Log in to reply
@Soumo Mukherjee – ok bro but sir is a term used for respect
Note: ∣ x ∣ isn't the variable. x is the variable.
∣ x ∣ 2 + ∣ x ∣ − 6 = 0 ⇒ ( ∣ x ∣ + 3 ) ( ∣ x ∣ − 2 ) = 0 .
But, ∣ x ∣ + 3 = 0 because ∣ x ∣ = − 3 (i.e ∣ x ∣ cannot be negative.)
Therefore, ∣ x ∣ − 2 = 0 ⇒ x = 2 o r − 2 . .
Clearly sum of roots is 2 + ( − 2 ) = 0 and product of roots is 2 × ( − 2 ) = − 4 . None of which are given in the options.
Hence the answer is (D) None of these ''.