Distance between furthest points on a specified trefoil curve.
The problem's question is: What is the distance between furthest points on a specified trefoil curve?
Points on the curve are { 2 sin ( 4 π t ) − sin ( 2 π t ) , − cos ( 2 π t ) − 2 cos ( 4 π t ) , − 3 1 sin ( 6 π t ) } where t ∈ [ 0 , 1 ) .
The answer proved not be what I had expected initially, the distance between the points on the curve most distant from the origin. It is slightly greater than that, which is 3 3 .
The answer is 5.48275162794062875804.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I solved it the same way you did, but somebody could also easily guess the answer, since you have told them that it is slightly greater than 3 3 . They could multiply that base value by 1.03, and if that doesn't work, multiply it by 1.03 again (since Brilliant has a 3 percent margin for decimal answers)
Log in to reply
@Steven Chase Sir, is this problem solvable by hand??? I tried but it seemed of no use to me........Also, I have observed that you solve problems easily using computer programs. Could you suggest a good book to start learning Coding from?? (Pertaining mostly to applications in Maths and Physics)....
Log in to reply
Hello. I can't say that it isn't solvable by hand, since I haven't proven that. But even if it is, it's probably too much effort. I'm sure there are good books on the subject of program-based problem solving, but that's not how I learned. I learned C++ in school, but really started writing a lot of code some years later when I picked up Python. The great thing about Python is that it is simple and free. I learned mostly by playing around and writing code.
In optimization problems, you can perform the standard "differentiate and set to zero" trick when solving by hand. Or with a computer, you can do a parameter sweep. In that method, you discretize the parameter space, vary the parameter over a range using a loop, and store the value which maximizes or minimizes an objective function. You can also use iterative approaches (like Newton-Raphson) to do the same thing more efficiently (but with more setup work).
You can also replace anti-differentiation (hand analysis) with numerical integration, which is hugely useful. Essentially, you are just straightforwardly computing a discrete Riemann sum, with Riemann sums being the first thing they teach in integral calculus classes (many of them, at least). With numerical integration, I would recommend looking into the Euler integration technique. It is the simplest and most intuitive method (although not the best). I will post a problem for this, which explains how to do it.
Log in to reply
@Steven Chase – In my case, I have been using Wolfram Mathematica (Version 12 currently). Although, it is an expensive package, there are legal ways to get it inexpensively -- it is included free in the Raspbian operating system on Raspberry Pi computers, which can be purchased as cheaply as US$5. This is because Stephan Wolfram made it available to the Raspberry people.
Here is a list of some computer algebra systems , many of which are open source or free.
In this problem, I used a numerical maximization procedure. I do not have a closed form solution.
First of all, this is a very pretty curve! Thanks for sharing.
Secondly, a couple of observations that help with solving (if I can work these into a full solution I will, but they need firming up):
- if the parameters ( t 1 , t 2 ) correspond to a pair of maximally separated points, then so do ( t 1 + 3 1 , t 2 + 3 1 ) . You can verify this numerically from your results, but the reason is the curve's threefold (trefoil?) symmetry
- as you've observed, if t appears in your list, so does 1 − t
Combining these, there is a maximally separated pair (please tell me a better way of wording this if you have one!) ( τ , 3 1 − τ ) with 0 < τ < 6 1 . Again, this can be verified numerically from your results.
This makes searching somewhat easier; instead of a two variable problem it is now just one variable. I haven't found an analytical solution, but that doesn't mean one doesn't exist!
The firming up that's needed before this is actually a solution is justifying the second observation. I only noticed it after solving the two variable problem numerically. Is there a justification that I'm missing?
You are correct. They could guess the answer that way. Would they learn anything that way? My purpose is that the obvious answer is not the correct answer in this case. The first iteration would have given an answer that was close enough .
All of the points are 3 n ± τ where τ is the same for all points. Actually it is not necessary to stay within the [ 0 , 1 ) interval; the trigonometric functions will take care the reduction to the interval.
I could not find an analytical solution either.
The first two images are a stereo-optic pair of the trefoil. The third image is a side view. The colors encode the z value of the trefoil.
Here is a view with the three solution lines plotted with the trefoil.
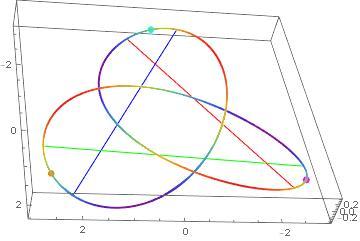
I solved in the two variable form and therefore did not worry about the second observation.
I found the answer by searching for sets of points yielding maximum distance. I found three pairs of such points, using t values: 0.029738945872856085 and 0.30359438738355093, 0.36307227921000046 and 0.6369277207314614, and 0.6964056125727761 and 1-0.029738945872856085.