Distance of closest approach
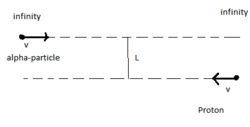 A proton and an
α
-particle are projected with velocity
v
=
4
π
ε
0
m
L
e
2
each from infinity as shown.The perpendicular distance between their initial velocities is
L
.Let the distance of their closest approach be
D
.
A proton and an
α
-particle are projected with velocity
v
=
4
π
ε
0
m
L
e
2
each from infinity as shown.The perpendicular distance between their initial velocities is
L
.Let the distance of their closest approach be
D
.
Given x = ( L 8 D − 5 ) 2 .Find x
Details and assumptions
1)mass of proton= m ,charge= + e
2)mass of α -particle= 4 m ,charge= + 2 e
3) ε 0 =Vacuum Permittivity
The answer is 89.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
please post the answer on brilliant. I don't find answer by the given link
Log in to reply
I will help:
m 1 a 1 = F 1 2
m 2 a 2 = F 2 1
Let F 1 2 = − F 2 1 = f ( r )
Now if we go into m 2 's frame of reference we have inertial force on \(m_1) so second Newton's Law:
\(m_1 a_{rel} = f(r)-m_1 a_2\)
m 1 a r e l = f ( r ) − m 1 m 2 − f ( r )
which is
m 1 a r e l = f ( r ) m 2 m 1 + m 2
m 1 + m 2 m 1 m 2 a r e l = f ( r )
Let m 1 + m 2 m 1 m 2 = μ Integrating this equation we will get equation of energies:
2 1 μ v r e l 2 + V ( r ) = c o n s t
Where V ( r ) is potential energy, similarly you can prove angular momentum conversation in form:
r v r e l = c o n s t
I tried something like this T1=mv^2/2+4mv^2/2 T2=mv1^2/2+4mv1^2/2 L1=L2 mvL=mv1D
T1-T2=k*2e^2/D
Can anyone tell me whats wrong here ?
If we use the conservation of energy and if we assume that the two charge do not radiate during deceleration(which seems to be a pretty good assumption in this case) then D=0.8L and that means X=1.96. What is wrong with this????????????????Can you explain this ???????
Please can you explain why did you take the system as reduced mass system and its initial velocity to be 2v. Things are unclear in the thread posted. I will appreciate if you could please explain in detail about the assumptions.
Or is there any other method.
I made the following equations-
1)energy conservation
2)conservation of momentum(in vertical and horizontal direction)
Log in to reply
Yeah i did it using the method used by you only! :)
Log in to reply
For the distance of closest approach they should lie on a vertical line
Log in to reply
@Prakhar Bindal – I didn't get it why they will lie in a Vertical line?
@Prakhar Bindal – I think minimum distance would be when velocity is perpendicular to the direction of force between them
I solved this in the method based on the following assumptions.1)For closest distance their velocity along the line joining them must be zero.2)Momentum conservation along the x,y directions.3)Energy conservation.4)Conservation of angular momentum about the centre of mass.This yielded 1 0 0 x 2 − 2 5 x − 4 = 0 .where ( x = D / 5 L ) .So the answer came out to be 8 9 . Although conservation of momentum along x,y is quite apparent better method would be to conserve it along radial and tangential directions.
It seems to be very heavy try doing the calculations by sitting on one of the particle and observing the motion of another particle. In this frame conserve angular momentum and apply energy conservation. It simply Comes out to be 89
Log in to reply
Seems heavy but isn't.Note that one could conserve momentum along radial and tangential directions.....I took time getting the idea but solved it quickly then
Please write solution in detail
it is a closed system therefore angular momentum in centre of mass frame isconserved about any point hence we can chose it about alpha particle by this we can solve question in 4 steps
Log in to reply
Better post a solution.....its not about having the shortest solution but thinking in various ways to solve a problem... Students at IMO write abt 11 pages for a solution(some tough ones) and they are still acknowledged even if there exists a single clean trick to crack the problem in a few pages......
As usual, a two-body problem like this (i.e. with a potential depending on the relative position of the particles) can be cast as a problem of a single particle subject to a potential. One needs just to choose the centre-of-mass frame, in which the Lagrangian is the following: L = 2 1 μ ( r ˙ 2 + r 2 ϕ ˙ 2 ) − 2 π ϵ 0 r e 2 , where r and ϕ are the polar coordinates of the relative position between the α -particle and the proton and μ ≡ m + m α m m α = 5 4 m is the reduced mass.
Now, it is not difficult obtain the Euler-Lagrange equations of motion and to integrate them once, obtaining: E = 5 2 m r ˙ 2 + 8 m r 2 5 l 2 + 2 π ϵ 0 r e 2 , where E is the energy and l ≡ μ r 2 ϕ ˙ , is the angular momentum. Both E and l are constants of the motion.
Now we use the data that the problem provide. The energy is given by the sum of the kinetic energies of the particles at infinity: E = 5 2 m r ˙ 2 = 5 2 m 4 v 2 = 5 π ϵ 0 L 2 e 2 , where recall that the relative velocity is twice v .
Similarly, the angular momentum is given by l = μ L 2 v = 5 8 m L v .
Now, we substitute these result in the equation we found above for the energy. The closest approach distance is given by the condition r ˙ = 0 , since this is a turning point. In other words, the relative position decreases from infinity to D as the particles approach and then starts to increase again.
Therefore, we have, after some algebra: L 2 D 2 − 4 L 5 D − 1 = 0 . In order for the x defined in the problem to appear, we must multiply by 64 and add 25. This leaves the result: x = 8 9
http://www.physicsforums.com/showthread.php?t=763108 Watch this link to get the answer.