Distances in a Right Triangle
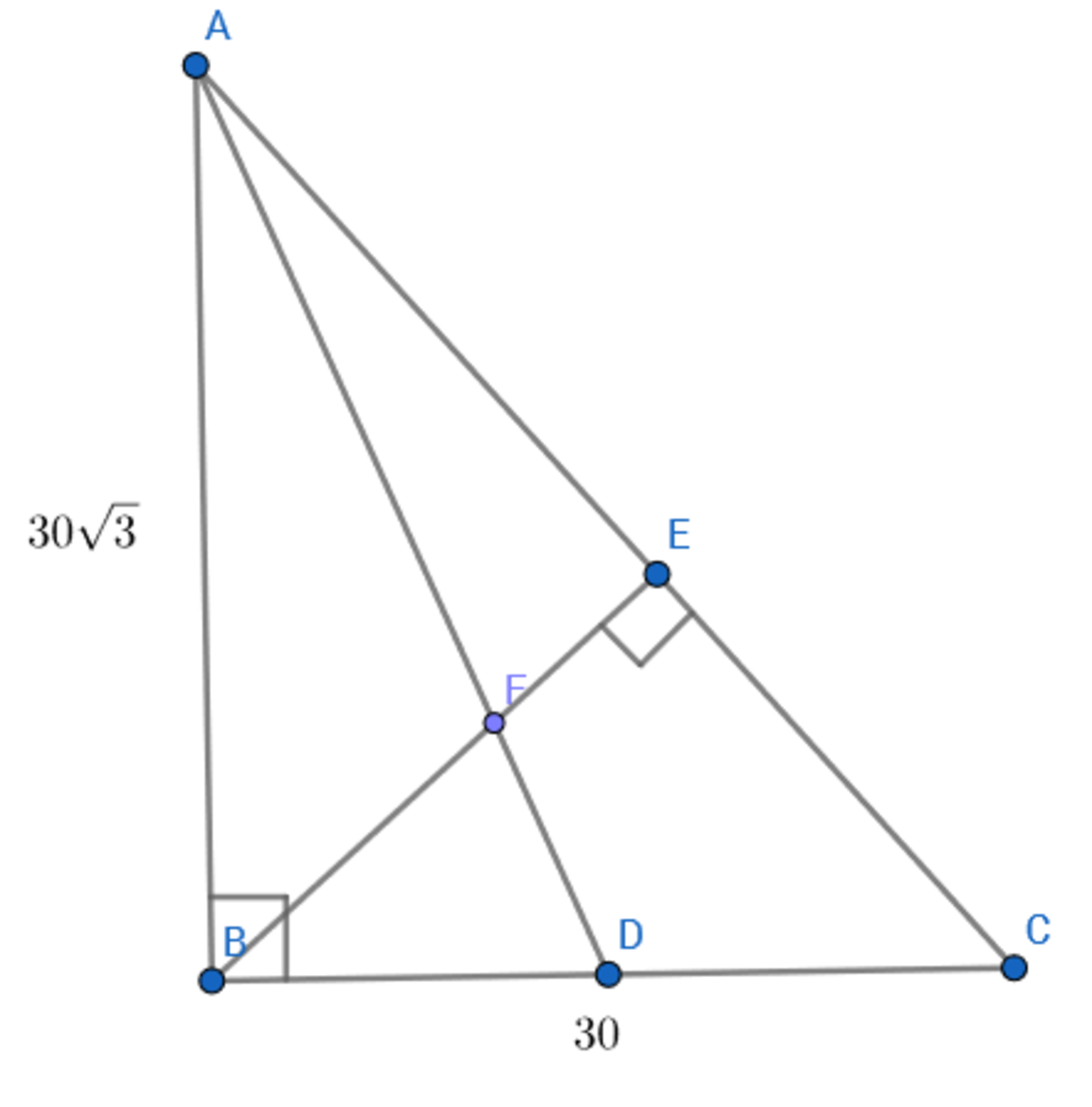
A B C is a right triangle with ∠ A B C = 9 0 ∘ with A B = 3 0 3 and B C = 3 0 . D is a point on segment B C such that A D is the median. E is a point on segment A C such that B E is perpendicular to A C . A D and B E intersect at F . If E F = c a b , where a and c are positive, coprime integers and b is not divisible by the square of any prime, what is the value of a + b + c ?
The answer is 55.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Did the same!!
Dang I did this right until 'from D drop a perpendicular'.... ok i get it.
I too used absolutely the same steps, using for 30-60-90 the side rations 1: 3 :2.
Almost the same solution, but I used little trigonometry :)
Key Ideas :
(1). Form equation of lines AD and BF and then find their point of intersection E.
(2). Using distance formula find EF.
Calculations:
To form the equation of straight line AD using two point formula- Take BC along x axis and B as origin, find points A and D. It will come out to be A (0, 18 3 ) and D (9,0).
To form the equation of straight line BF - If you know how to find the foot of a perpendicular from a point on a straight line find point F and hence equation BF
Otherwise, use the the slope point formula to derive the equation of BF. Note that to find the slope of line BF you can use the fact that BF is perpendicular to AC.
After finding the equations of both the lines find their point of intersection E.
Finally, using the distance formula find distance between the point E and F and hence you have EF which is required in the question.
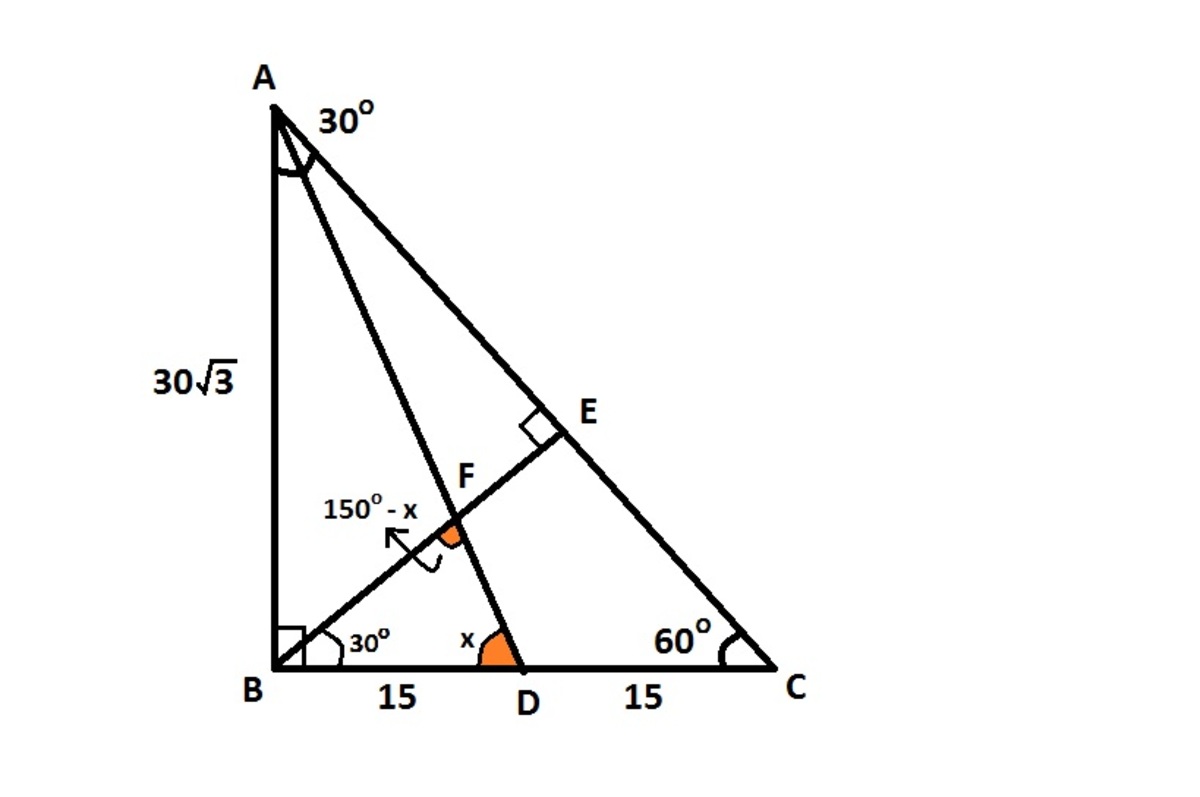
We find B E first using area of the triangle. 2 1 × B C × A B = 2 1 × A C × B E
Using A C = A B 2 + B C 2 , we get B E = 1 5 3
Now, tan ( x ) = B D A B = 2 3 . So, sin ( x ) = 1 3 2 3 and cos ( x ) = 1 3 1
Using sine rule in Δ B F D , we get 1 5 sin ( 1 5 0 o − x ) = B F sin ( x ) which upon expanding and solving gives us B F = 7 6 0 3
Finally, E F = B E − B F = 7 4 5 3
And, of course, 4 5 + 7 + 3 = 5 5
AC=√[(30√3)²+30²]=60
From similarity, AE=45 and EC=15
Also in triangle ABD, AD=√[(30√3)²+15²]=√2925=15√13
Applying cosine rule in traingle ADC (taking angle DAC=∅)
cos∅= (AD²+AC²-CD²)/(2xADxAC)
cos∅= (2925+3600-225)/(2x15√13x60)=7/2√13
Which gives sin∅=√3/2√13 and tan∅=√3/7
In triangle AEF, right angled at E,
EF=AE tan∅=45√3/7
Hence a+b+c=45+3+7=55
Relevant wiki: Menelaus' Theorem
 In
Δ
A
B
C
,
In
Δ
A
B
C
,
By Pythagorus theorum, we have :
A C = ( 3 0 3 ) 2 + 3 0 2 = 6 0
In Δ A B C and Δ B E C we observe:
∠ B = ∠ E = 9 0 ∘
∠ C = ∠ C
Therefore Δ A B C ∼ Δ B E C
⇒ E C = 2 3 0 and B E = 1 5 3 so A E = 6 0 − 1 5 = 4 5
Now, In Δ B E C , D , F , A are externally colinear. So by Menelaus' Theorem ,
D C B D × A E C A × F B E F = 1
1 5 1 5 × 4 5 6 0 × F B E F = 1
F B E F = 4 3
and we also have E B = E F + F B = 1 5 3
⇒ E F = 4 5 7 3
So the answer is 5 5 .
Simple calculations yield A E = 2 7 , B E = 9 3 , and CE = 9. Thus AE/CE = 3, and BD/DC = 1. We assign a mass of 1 to A, so B and C get masses of 3, E has a mass of 4, and D has a mass of 6. Thus EF/FB = 3/4, so EF/EB = 3/7. Thus E F = 3 / 7 × 9 3 = 2 7 3 / 7 , so the answer is 37.
[Note: There wasn't a need to calculate the mass at D.]
There are numerous ways to approach this problem, ranging from similar triangles, construction of a point, coordinate geometry, area of triangles, parallel lines, etc.
Using mass points (as in Kevin's solution) helps to simplify the calculations, and we can get a simple result extremely quickly.
@Calvin Lin Is this solution correct?
Log in to reply
Yes it is. As stated,
Using mass points (as in Kevin's solution) helps to simplify the calculations, and we can get a simple result extremely quickly.
Log in to reply
@Calvin Lin The answer is 55.. not 37
Log in to reply
@Abhijeet Verma – This is an old problem from back in the day when we allowed for different values to be used in problems. We have since fixed it, and so the solution is to a slightly different problem. Let me bump this down so that it's not too confusing.
First, we use the trig operator tan and cos respectively over ∠ B A E to find that ∠ B A E = 3 0 ∘ and A E = 4 5 .
Now we let ∠ E A F = θ which implies that ∠ B A D = 3 0 ∘ − θ . Therefore, tan ( 3 0 ∘ − θ ) = A D B D = 6 3 .
Using the angle subtraction formula for tangent ,we solve that, tan θ = 7 3 . Since △ A E F is also right angled we conclude that, E F = A E × tan θ = 7 4 5 3 and hance the ans is 4 5 + 3 + 7 = 5 5

Applying the Pythagorean theorem on triangle A B C , we have A C = A B 2 + B C 2 = ( 3 0 3 ) 2 + ( 3 0 ) 2 = 6 0 . Thus C B A is a 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangle as C B : B A : A C = 1 : 3 : 2 . Therefore ∠ A C B = 6 0 ∘ and ∠ B A C = 3 0 ∘ . This implies that ∠ E B C = 3 0 ∘ and so triangle B E C is a 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangle. Hence E C = 1 5 and B E = 1 5 3 . Thus it follows that A E = A C − E C = 6 0 − 1 5 = 4 5 .
From D drop a perpendicular to A C at G . So, we have that triangle D G C is a 3 0 ∘ − 6 0 ∘ − 9 0 ∘ triangle, thus D G = 2 1 5 3 and G C = 2 1 5 . Hence A G = A C − G C = 6 0 − 2 1 5 = 2 1 0 5 . We also have that triangles A E F and A G D are similar by angle-angle-angle. Thus A E E F = A G D G ⇒ E F = A G A E ⋅ D G = 2 1 0 5 4 5 ⋅ 2 1 5 3 = 7 4 5 3 . Hence a + b + c = 4 5 + 3 + 7 = 5 5 .