Divide 10 circles

Geometry Level 1

10 identical circles are stacked in a pyramid shape, where $A$ and $B$ are centers of two of the circles. A line is drawn through $A$ and $B,$ dividing the figure into 2 areas: red on the left and and blue on the right.

What is the ratio of the red area to the blue area?

{\color{#D61F06}3}:{\color{#3D99F6}4}

{\color{#D61F06}2}:{\color{#3D99F6}3}

{\color{#D61F06}3}:{\color{#3D99F6}5}

{\color{#D61F06}1}:{\color{#3D99F6}2}

8 solutions

Calvin Lin Staff
Nov 21, 2017

Consider the addition of the 4 circles with a black outline. Since the figure is now rotationally symmetrical, there must now be an equal area of red and blue. With 14 circles, there is now 7 red and 7 blue circles, which means that there previously was $7 - 3 = 4$ red and $7 - 1 = 6$ blue circles.

Hence, the ratio is $4 : 6 = 2 : 3$ .

Moderator note:

This solution exploits the inherent symmetry in the problem to justify that the "parts can be replaced".

This approach also works in cases where the parts cannot be replaced nicely, but the images are still on a grid.

Different rotation argument.

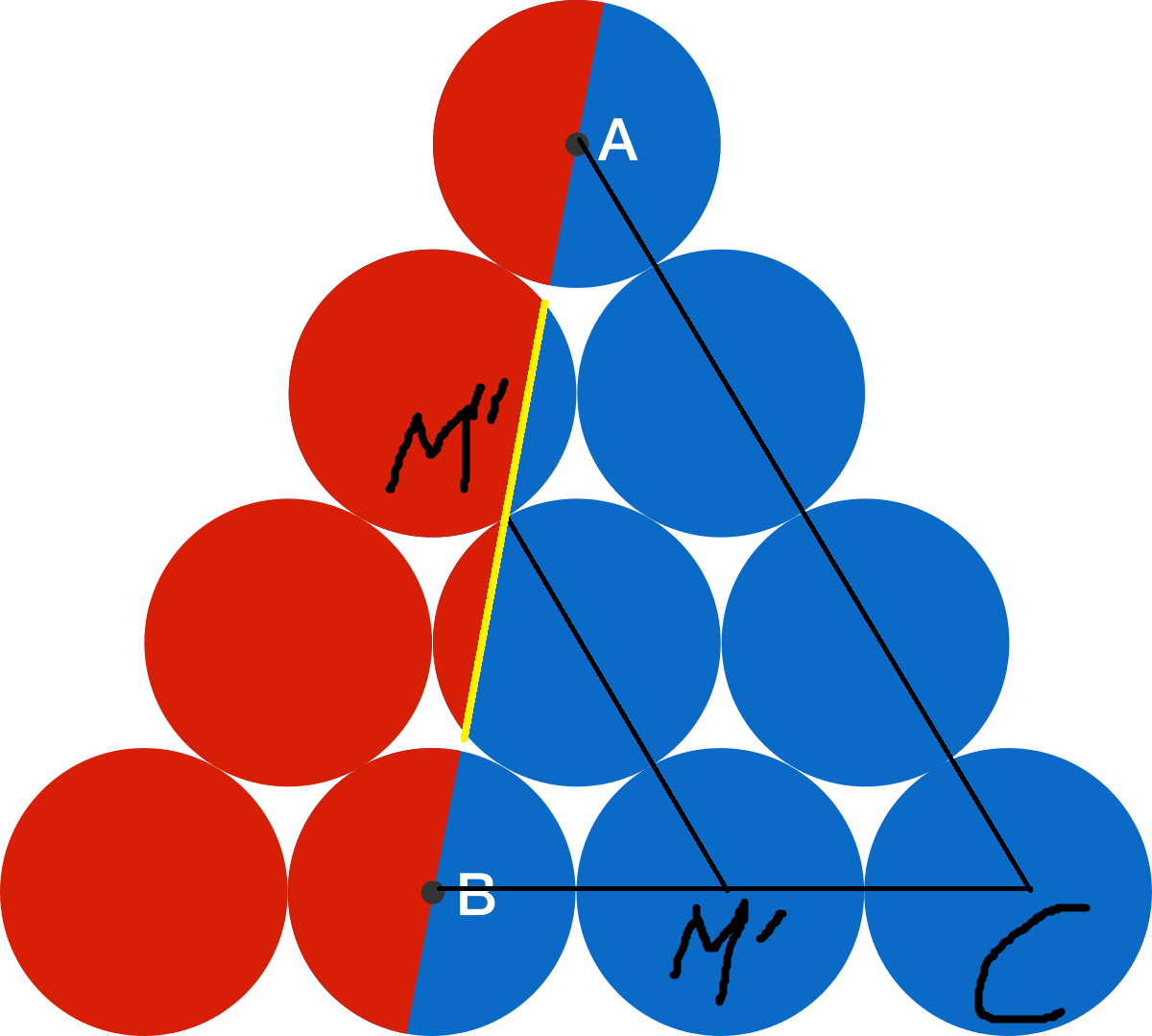
Define C so it is at the center of a center of the circle. Define M' so that it divides BC in two and is the center of a circle. Define M'' to be the point where the two circles meet. Now notice that when translating the line AC and placing it on M'M'' they on each other and are parallel. If M' is at the center of BC then triangle BM'M'' is similar and is twice as small as triangle ABC by similar triangles (the fact the lines AC and M'M'' are parallel BM'). Since ABC and BM'M'' are similar then the line AB is split in half by M'. This means the yellow line is split in half by M'. This means that if M' acts as a point of rotation then the mostly red circle can be rotated to fit on the mostly blue circle showing their segments are equal.

It can then easily be shown that the area is split by the ratio of 3:2. (The small red segment fits perfectly on the small blue segment and the small blue segment fits perfectly on the small red segment to lead a much simpler case)

Mo H - 3 years, 6 months ago

Just realized, the rotation argument used here adds no simplicity. Since the circles are all the same then merely proving that the yellow line is bisected and the segments have the same chord length then the segments are equal in area.

Mo H - 3 years, 6 months ago

Essentially, you want to argue about the symmetry around point $M''$ . That is also the point where my figure is rotationally symmetrical.

Your approach presents good details about why "the areas will fit into each other".

Calvin Lin Staff - 3 years, 6 months ago

Hana Wehbi
Nov 10, 2017

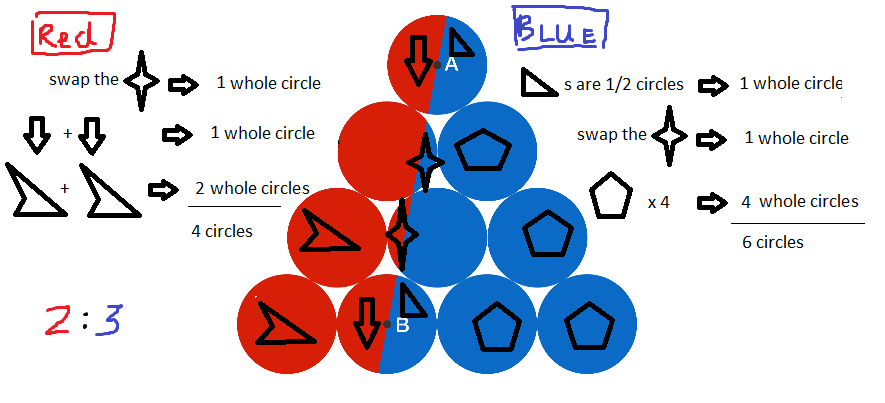
From the image, you can tell the parts I replaced; thus, Area of $\frac{B}{R} = \frac{6 \text { blue circles}}{4 \text { red circles}}= \frac {3}{2} = 1.5$

How do you know that the parts can be replaced?

I agree that for the top and bottom circles, since the line passes through the center, hence we have 2 halves of the circle. For the other 2, there needs to be an explanation.

Calvin Lin Staff - 3 years, 6 months ago

Ok, l will try another solution. Thanks for letting me know.

Hana Wehbi - 3 years, 6 months ago

Parts must be replaceable since the line goes through center of two out of 10 evenly spaced out circles, which are all the same radius.

pero kvrgo - 3 years, 6 months ago

it can easily be measured by measuring length of the line inside the circles and measuring radius of circles.

pero kvrgo - 3 years, 6 months ago

We don’t need measuring. Since all circles are congruent and the line goes through the center of two of them so the parts divided will be congruent as well.

Hana Wehbi - 3 years, 6 months ago

@Hana Wehbi – Yes thats what im saying...But i guess someone removed the comment where they were asking themselves if the parts are replaceable and how can they be sure...

pero kvrgo - 3 years, 6 months ago

@Pero Kvrgo – I guess my ''measuring'' comment was supposed to be reply to Calvin Lin's comment... Its interesting that Staff is clueless...

pero kvrgo - 3 years, 6 months ago

@Pero Kvrgo – Ok, no problem.

Hana Wehbi - 3 years, 6 months ago

Zain Majumder
Nov 20, 2017

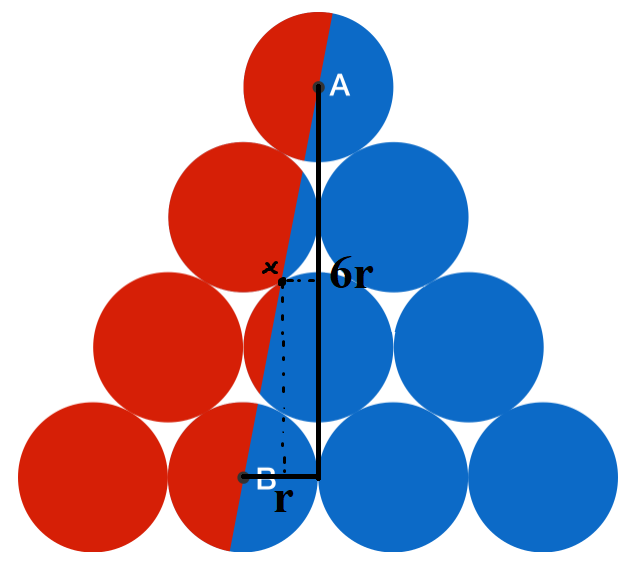
Circles $A$ and $B$ are divided into two semicircles. We can swap the red half in circle $A$ with the blue half in circle $B$ to create a red and blue circle.

If the radius of one circle is $r$ , the horizontal distance between points $A$ and $B$ is $r$ , and the vertical distance is $6r$ . The point of tangency $X$ is $3r$ above $B$ and $0.5r$ to the right of $B$ , so it must fall on $AB$ .

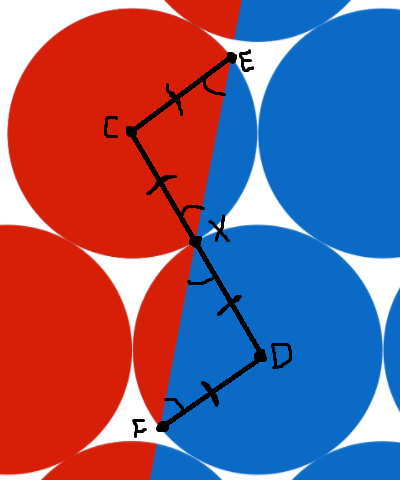
It seems that we may swap the red and blue pieces in these circles as well, but we need to prove that the small red and blue segments are congruent. $\angle CXE \cong \angle DXF$ since they are vertical angles. Both triangles are isosceles, so $\angle CXE \cong \angle CEX$ and $\angle DXF \cong \angle DFX$ . Therefore, $\angle ECX \cong \angle FDX$ , and so the red and blue segments must be congruent.

We can swap these two segments to create a new red and blue circle. Now, we have $6$ blue circles and $4$ red circles, so the area ratio is $6:4=\boxed{3:2}.$

While the second part of your argument is correct, I don't think that's 6r in the figure on top. Just draw horizontal lines from the bottoms of the circles and you can see.

John John - 3 years, 6 months ago

Good point. Don't know how I missed that :/ I don't know how to prove $RX$ is half the vertical distance.

Zain Majumder - 3 years, 6 months ago

Draw horizontal and diagonal lines which join the centers of the circles to form equilateral triangles, and note that the diagonal lines pass through the points of tangency. The vertical distance, rather than 6r, would be 3r sqrt 3. To show X is half this vertical distance below A, consider lengths of altitudes of various equilateral triangles.

Steve Shaff - 3 years, 5 months ago

Leonardo Bozza
Nov 20, 2017

There are ten circles in total, only one ratio adds up to 10, or at least a factor of 10, therefore that is the only valid option.

Moderator note:

As pointed out in the comment, this makes the assumption that the areas work out such that they can be rearranged as whole circles; this is not necessarily the case.

that is assuming that there is a whole number of circle area in each part

Josh Willwerth - 3 years, 6 months ago

A Former Brilliant Member
Nov 23, 2017

I thought quite randomly. There are 3 full circles in the blue area without the line intersecting them. In the same way the red part has 2 full circles. Other parts are negligible. That's why I thought 3:2 😁 I know it seems legit.

Michael Fitzgerald
Nov 21, 2017

Simple! This was exactly my way of thinking too :-)

Malin de Koning - 3 years, 5 months ago

Number the circles from 1 to 10 beginning with the top circle as 1, those in the next row are 2 and 3 from left to right, etc. Now consider the area ratio red : blue in stages as follows: circles 1 and 7 balance each other in a ratio 1 : 1. Circles 2 and 5 also balance each other, so the ratio now becomes 2 : 2. There are now 2 red circles and 4 red circles remaining, so the final ratio is 4 : 6, or 2 : 3. Done.

Steve Shaff - 3 years, 5 months ago

Samuel Walker
Nov 21, 2017

Due to the rotational symmetry along the line, the area of the 2 red segments will add to 1 and the 2 red semicircles will also be 1. The same can be applied to the blue circles and simple addition will give you an answer of 6:4, or 3:2.

Sayantan Mondal
Feb 28, 2018

As the circles have been replaced with the blue and red parts we can just add up then and have the ratio as 4:6 that is 2:3

Divide 10 circles

8 solutions

Moderator note:

Moderator note:

0 pending reports