Attack Cities and Conquer
As Sheldor the conqueror, you're supposed to conquer the kingdom of Wonder-blunder-berg , which happens to be a collection of cities connected with roads.
Your first plan is to attack cities, which when blocked, splits the kingdom into parts that cannot communicate with each other.
For example,
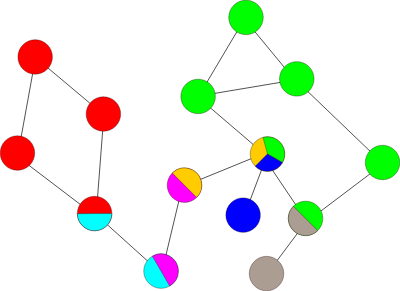
In the above kingdom, the multicolored cities, when removed, disconnect the road network.
This is the Adjacency List of the road network of Wonderblunderberg showing which city has a direct road to which other city.
How many such vulnerable cities exist in the kingdom?
Clarification: A component is a maximal set of cities such that there is a walk between any two cities of the set. A vulnerable city is a city which when, along with its roads, removed, increases the number of components.
The title is just a title, it has nothing to do with the algorithm you'll need.
Image Credit: Wikimedia Zyqqh .
The answer is 28.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Agnishom Chattopadhyay : In your "Carrot" problem file, some of the x-coordinates have value 1000. Is that an error?
Log in to reply
Yes, can you disregard those points and let me know what answer you are getting?
Log in to reply
@Agnishom Chattopadhyay : Sure. If I could at all solve it ;)
Log in to reply
@Snehal Shekatkar – I am sorry about the error. I will try to fix this soon.
Hi; Only Agnishom could get me to think about graphs.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
|
Nice brute force approach and thanks for posting it here. :)
Let me clear up a few misconceptions you have: The original graph was
not
connected. When you ran
g = Graph[rules, VertexShapeFunction -> {"Circle"}];
, you removed the vertices without the edges. What you should have run was
g = Graph[Range[274], rules];
Count[ConnectedGraphQ[VertexDelete[g, #]] & /@ (VertexList[g] // Sort), False]
is not what we meant by a Vulnerable City, although you are close. Because the only components other than the large network were the isolated vertices, you got away with this.
Here is the foolproof Mathematica code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
|
Hi Agnishom;
Had I even noticed those vertices without edges, I would have removed them. But you are correct, the original graph is not connected.
A few misconceptions? Ah ha, I got ya! I have thousands of misconceptions. As you well know, I am not good with Mathematica. Coupled with my inexperience with graphs (second graph theory problem I ever worked on ) we now see why I produced kaboobly doo. Yep,I got lucky, again, it is the secret I do not tell anyone.
Thank you for the code, I will need to study it for a couple of years.
This solution is based on this idea:
We remove one city a from the graph.
if the cities previously connected to a are not in the same component , this is a vulnerable city.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
|
In Graph Theory, we call such vulnerable points Cut Vertices or Articulation Points . In the following analysis, we'll assume that the graph is connected. If it is not, we run the algorithm separately for each component.
We could explore our graph using Depth First Search . While doing so, we could think of a spanning tree called the DFS tree . In the DFS tree ,
The non-tree edges are classified into forward edges, backward edges and cross edge depending on the depths they connect.
Consider this graph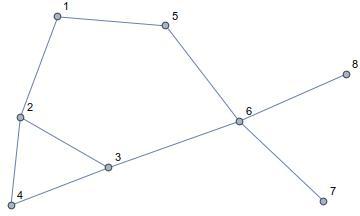 and its corresponding DFS tree
and its corresponding DFS tree
We define a concept called the lowpoint of a vertex. For each vertex v , the lowest depth of neighbors of all descendants of v in the DFS tree is l o w p o i n t ( v ) . For example, the lowpoint of 2 in this graph is d = 1 , since one of its descendants have a backedge to a vertex at depth 1.
Now lets take a graph and draw its DFS tree. If there is a child v of a vertex u such that there is a back-edge from v to u or its ancestors, then v is not an articulation vertex. That is because, even if v were removed, that backedge would still be keeping the graph connected. So, if v is a (non-root) articulation point, v has a child such that l o w p o i n t [ y ] ≥ d e p t h [ v ] .
The root needs to be dealt separately. The root is an articulation point iff it has more than one children.
Alright, time for action.