Diving Cone
A solid right circular cone of uniform mass density is initially at rest above a body of water, so that its vertex is just touching the water's surface with its axis of symmetry along the vertical.
Now, the cone falls into the water, and has zero speed at the instant it becomes fully submerged. What is the ratio of the density of the cone to the density of the water? Submit your answer to 2 decimal places.
Details and Assumptions:
- There is an ambient downward gravitational field.
- Assume that the buoyant force is the only force exerted by the water on the cone.
The answer is 0.25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Very nice solution.
You could include the observation that the kinetic energy is zero at the beginning and the end of the process, and then use the conservation of energy explicitly.
Log in to reply
Thanks, I'll add it.
Log in to reply
Hi Rohit,
There is another wrinkle to this problem - we have to assume that no energy has been carried away by the spreading waves in the fluid.
Calculating this is so far beyond a level 2 problem that we can assume we are intended to ignore it, but this should really be stated in the assumptions of the problem!
Log in to reply
@Peter Macgregor – I think assumption #2 already covers this.
Log in to reply
@Steven Chase – @Peter Macgregor , the assumption is only about the force exerted by the water on the cone. While it tells nothing about forces exerted by the water elsewhere. Of course it does not mind in this particular case, as said @Rohit Gupta .
@Rohit Gupta I understood what m w a t e r d i s p l a c e d g 4 h means. But what is m c o n e g h ? What does it quantify?
Log in to reply
m cone g h is the loss of potential energy of the cone when it enters into the water.
Let us call:
- m as the cone mass
- R as the cone base radius
- H as the cone height
- y as the portion of the cone height which is submerged
- r as the radius of the base of the cone sector which is submerged
- v as the cone vertical velocity downwards
- ρ H 2 O as the water density
- ρ c o n e as the cone density
First, by triangle similarity:
r = H R y
Writing the differential equation of the cone:
m d t d v = m g − ρ H 2 O g 3 π r 2 y
d t d v = g − ρ H 2 O g 3 m H 2 π R 2 y 3
Let us define:
k ≜ ρ H 2 O g 3 m H 2 π R 2
d t d v = g − k y 3
d y d v d t d y = g − k y 3
d y d v v = g − k y 3
v d v = ( g − k y 3 ) d y
Since at y = 0 , v is also 0 (cone begins at rest):
∫ 0 v v d v = ∫ 0 y ( g − k y 3 ) d y
2 v 2 = g y − 4 k y 4
At y = H (instant in which cone fully submerged), v is also equal to 0 :
0 = g H − 4 k H 4
H 3 = k 4 g
H 3 = 4 g π R 2 g ρ H 2 O 3 m H 2
3 π R 2 H m = 4 ρ H 2 O
ρ c o n e = 4 ρ H 2 O
ρ H 2 O ρ c o n e = 4 1 = 0 . 2 5
We posted same solutions at same time!!!!
Nicely explained! Does this mean that the answer does not depend on the angle of the cone?
Same!! I love solving these types of problems using calculus
applying thekinetic energy theorem
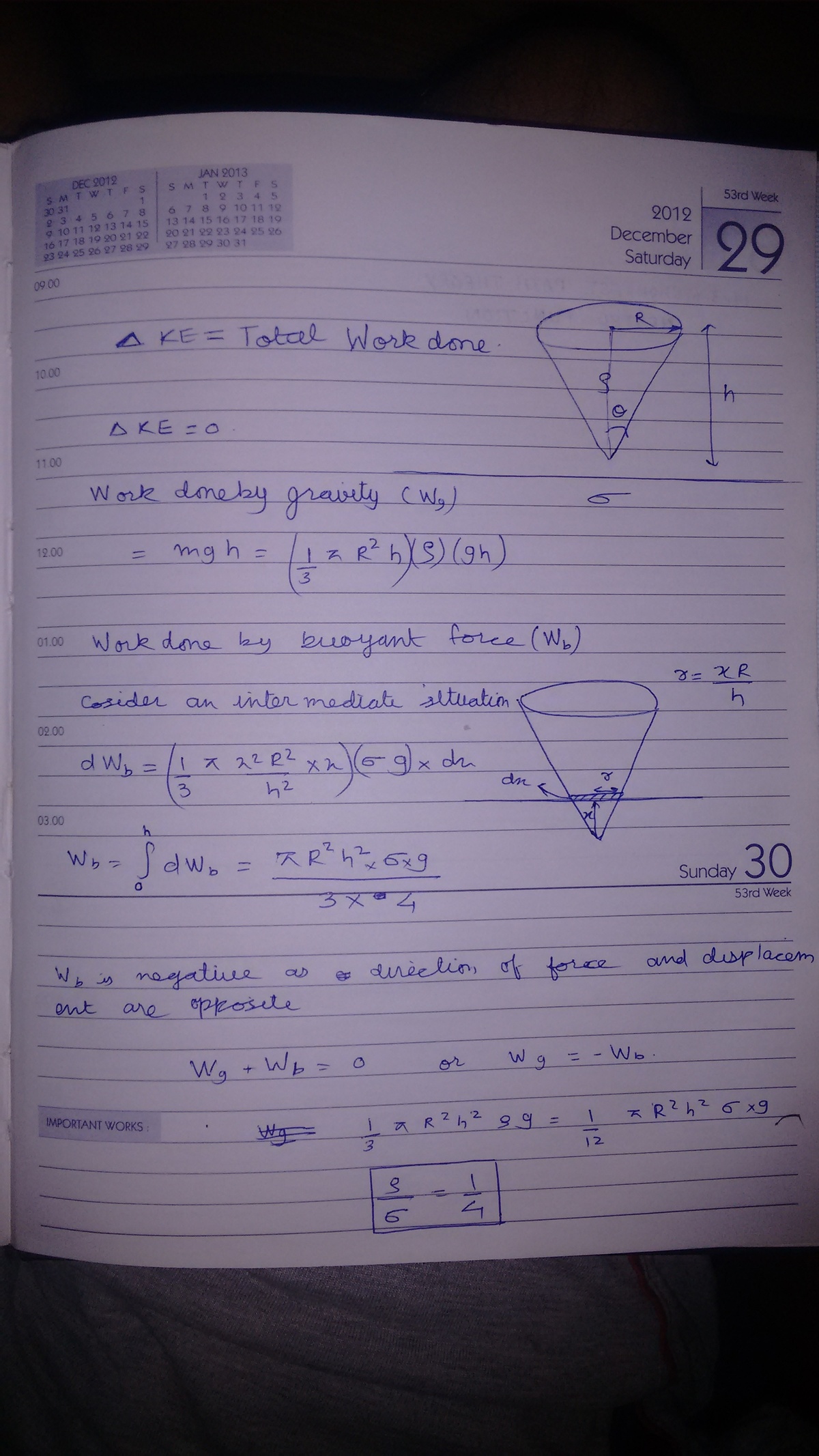

I didn't get how you found the expression for d W b . Could you explain how you found out the magnitude and direction of the force?
@Pranshu Gaba please refer the edited solution. If required refer the figure in first picture
Log in to reply
Thanks, it is clear now :)
Log in to reply
@Pranshu Gaba I'm really fond of your problems!!!
I noticed that the acceleration depends on x 3 , which looks very similar to simple harmonic motion. Do you think the cone will oscillate in a periodic motion?
At the place where the cone ends up, there is initially water. That water is pushed toward the surface. Thus the water gains potential energy in the amount Δ U w = m g y = V ρ w ⋅ g ⋅ 4 1 h = ( 4 1 ρ w ) V g h . The factor 4 1 is due to the fact that the center of mass of a solid cone lies at 4 3 from its vertex.*
Meanwhile, the cone loses potential energy because its center of mass drops the cone's height. Thus Δ U c = − m g h = ρ c V g h . Since the mechanical energy is conserved and no kinetic energy was gained or lost, we have Δ U w + Δ U c = 0 ∴ 4 1 ρ w = ρ c , showing that the cone's density is 0 . 2 5 times the density of the water.
- Proof: let the radius of the cone by R and the height h . Divide the cone into infinitesimal disks; the disk at height y will have radius r ( y ) = R y / h . Therefore ⟨ y ⟩ = ∫ 0 h r 2 d y ∫ 0 h y r 2 d y = ∫ 0 h ( R y / h ) 2 d y ∫ 0 h y ( R y / h ) 2 d y = ∫ 0 h y 2 d y ∫ 0 h y 3 d y = 3 1 h 3 4 1 h 4 = 4 3 h .
What happens after the cone has fully submerged and has come to rest?
Log in to reply
It will start moving upward. If there it no friction (quite unrealistic under water!), the cone will pop up out of the water, to its original height. If it does not tip over (quite unlikely as it is top-heavy!), it will fall back. Thus, without friction the cone would theoretically oscillate up and down between the two extremes.
In reality, accounting from friction, the cone will eventually come to a rest, with its tip pointed down, at its point of minimum potential energy, which means 75% of its volume sticking out above the water.


Relevant wiki: Conservation of Mechanical Energy
We know that the center of mass of a right circular cone is at a height of 4 h from the base. When the cone goes into the water, the water displaces and comes to the surface. Thus, the cone is losing the gravitational potential energy which is gained by the water. The kinetic energy is zero at the beginning and the end of the process, thus using the conservation of energy, we get.
m cone g h = m water displaced g 4 h
m water displaced m cone = ρ water ρ cone = 4 1 = 0 . 2 5