Divisible by 3?
How many of the following numbers are divisible by 3?
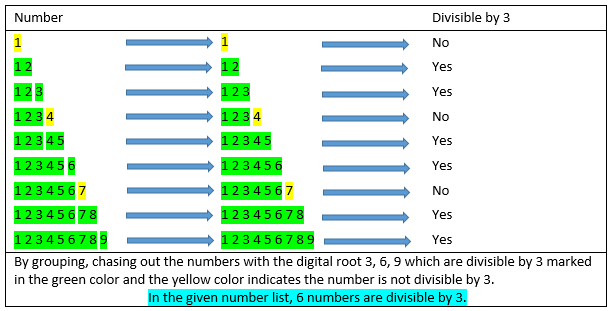
1 1 2 1 2 3 1 2 3 4 1 2 3 4 5 1 2 3 4 5 6 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Hi Venka, great explanation. I like the visual aspect which makes your explanation immeidately apparent.
To check for divisibility of 3, you must add the digits of the number and if the digital sum is divisible by 3, then the number is divisible by 3.
Checking each of the digital sums,
1 − 1 not divisible by 3
1 2 − 1 + 2 = 3 divisible by 3
1 2 3 − 1 + 2 + 3 = 6 divisible by 3
1 2 3 4 − 1 + 2 + 3 + 4 = 1 0 not divisible by 3
1 2 3 4 5 − 1 + 2 + 3 + 4 + 5 = 1 5 divisible by 3
1 2 3 4 5 6 − 1 + 2 + 3 + 4 + 5 + 6 = 2 1 divisible by 3
1 2 3 4 5 6 7 − 1 + 2 + 3 + 4 + 5 + 6 + 7 = 2 8 not divisible by 3
1 2 3 4 5 6 7 8 − 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 3 6 divisible by 3
1 2 3 4 5 6 7 8 9 − 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 4 5 divisible by 3
Therefore 6 of the above numbers are divisible by 3
Note: To calculate the digital sums you can use the formula 2 n ( n + 1 )
Divisible ( not diverse sable!! Autocorrect..) 😂
Save some work and when you know the previous number is divisible by three discard all those numbers. Good example is 1 + 2 + 3 + 4 + 5 = 15.
When you go to 6 you can forget about 1 - 5
When you go to 7 it fails since you discard everything before 6.
When you go to 8, 7 + 8 = 15
When you go to 9 discard everything before 9, so :)
10 is not, based on discarding everything before 10.
11 is because 10 + 11 is 21 and so on. Much less work.
Note below is based on adding everything before it:
12 good
13 bad
14 good
15 good
16 bad
17 good
18 good
You get the idea.
Log in to reply
I think what you want to say is that it's simpler if you keep a running total of the digital sum. Or, better yet, keep a running total of the digital sum (mod 3).
Log in to reply
No I mean that you forget about the preceding numbers in the sequence as soon as you find a sum that is divisible by three you only deal with the subsequent sum until you find something divisible by three.
So in computer thinking:
Scenerio 1: False (Sum = 1)
Scenerio 2: True (Sum = 3) which equals 0 mod 3 (that part is right)(conditionally Set Sum to 0)
Scenerio 3: True (Sum = 3) (Conditionally set sum to 0)
Scenerio 4: False (Sum = 4)
Scenerio 5: True (Sum = 9) (mod 3 = 0) set sum to 0
Scenerio 6: True (Sum = 6) set sum to 0
This is how I did it in my head. So without the computer this methodology was simpler for even high numbers you can continue to eliminate the preceding sum. Then you can use the 3 trick to test them no matter how big the number. So I eliminate part of the digital sum everytime I hit a mod 3 = 0 (sorry for the lack of equivalence symbols). But you are sort of correct. I thought the initial explanation was pretty clear anyways. The "Better yet" statement was definitely a more accurate portrayal of what was happening. But Computer Science is my field so I think of everything algorithmically. The outcome isn't as important as the efficiency of the method.
Log in to reply
@Eric Belrose – Mod 3 would be easier if implemented but mechanically unless you are a computer it is difficult to ascertain when the sum exceeds 4 or 5 digits. (I know not required for this question)
They are all diverse sable by three. Maybe not resulting in whole numbers, but that was not a requirement of the question.
Log in to reply
When you check whether a number is divisible, you always talk about resulting in whole numbers. No need to say that extra :)
In mathematics, "X is divisible by X" is defined as X is capable of being divided without remainder by Y.
The correct answer is 9. They are all divisible by 3 Only 6 are evenly divisible by 3..... But that is not what the question asked.
Moderator note:
In mathematics, " X is divisible by Y " is defined as X is capable of being divided without remainder by Y .
Mathematicians conventionally use the definition of divisibility in which the remainder is 0. https://brilliant.org/discussions/thread/number-theory-divisibility/
Because divisibility by 3 is the sum of the digits, we can check the sum of the digits for divisibility by 3. Instead of checking all the sums, we can recognize that the sum of consecutive digits (which these are) is n ( n + 1 ) / 2 . Hence divisibility occurs when either n or n+1 is a multiple of 3. This happens at 2,3,5,6,8,9 => 6 .
An integer is divisible by 3 only when the sum of its digits is divisible by three. For instance, 27 is divisible by 3 because 2+7=9 and 9 is divisible by 3.
- 1 - 1 and 1 isn't divisible by 3
- 1 2 - 1 + 2 = 3 is divisible by 3
- 1 2 3 - 1 + 2 + 3 = 6 is divisible by 3
- 1 2 3 4 - 1 + 2 + 3 + 4 = 1 0 is not divisible by 3
- 1 2 3 4 5 - 1 + 2 + 3 + 4 + 5 = 1 5 is divisible by 3
- 1 2 3 4 5 6 - 1 + 2 + 3 + 4 + 5 + 6 = 2 1 is divisible by 3
- 1 2 3 4 5 6 7 - 1 + 2 + 3 + 4 + 5 + 6 + 7 = 2 8 is not divisible by 3
- 1 2 3 4 5 6 7 8 - 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 3 6 is divisible by 3
- 1 2 3 4 5 6 7 8 9 - 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 4 5 is divisible by 3
Therefore, there are a total of 6 integers that are divisible by three from the list.
Actually all of these numbers are divisible by 3. Only six are EVENLY divisible by 3. Small distinction but an important one.
In mathematics, "X is divisible by Y" is defined as X is capable of being divided without remainder by Y.
Really all of them can be divided by 3, as the question does not specify that the answer is an integer...
In mathematics, if say, x is divisible by b , then b can fit into x with no remainder.
Relevant wiki: Divisibility Rules (2,3,5,7,11,13,17,19,...)
Using the below logic, we can use the previous calculation of the divisibility by 3 for the next number.