Divisible By 41
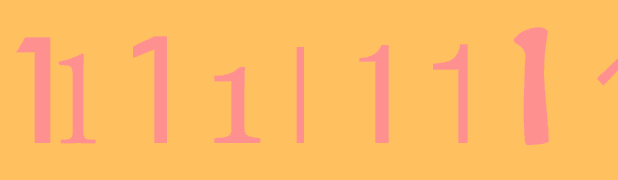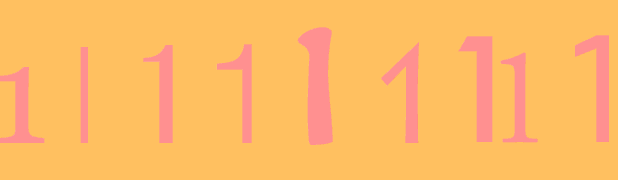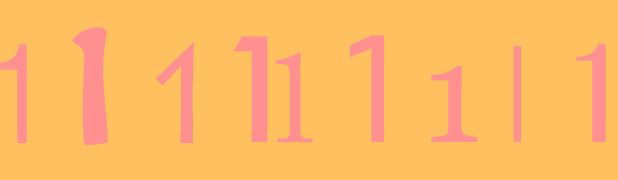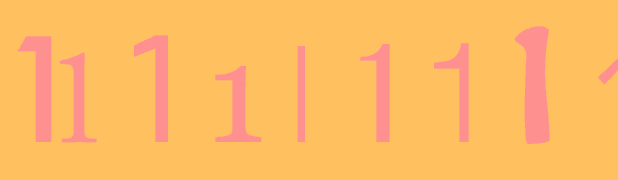 Consider all values of
n
such that the number
1
1
1
…
1
1
1
in which the number 1 occurs
n
times is divisible by 41.
Consider all values of
n
such that the number
1
1
1
…
1
1
1
in which the number 1 occurs
n
times is divisible by 41.
What is the largest integer which must be a factor of n ?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
I used the method to multiply of elementary school student. I'm new here, and I don't find a how to present this kind of method.
-
You see that for the result to be all one, the first number must be 1. So you have the upper line 1, and the second line 4x1=4. Pic
-
For the result to be 1, the upper line must be 7 Pic Therefore the next number on the second line is 8, because 4x7 = 28 (write 8, keep 2)
-
Remember that your previous calculation, 4+7 =11, not 1, so you must keep 1. Therefore the number on the first line is 2 (2 + 8 = 10, and add your 1 is 11. Write 1, keep 1) Pic
-
4x2=8, and add 2 from the 4x7=28 calculation, you have 10. Write 0, keep 1. Remember the previous calculation, 2+8+1=11, you kept 1, so you have to make the sums of the row to 10 to make 10 +1 =11. However, you can't do that with a 0 on the bottom line. The upper line therefore will be 0 too, so 0 + 0+1=1 Pic
-
4x0=0, and add 1 from the 4x2+2 = 10, you have 1 on 2nd line. Aware that you only did 0+0+1 =1 in the previous calculation, and no keeping. Thus, you have to add up to 11 or 1 this time. You can't add to 11, so you add 0 to make 0+1=1 Pic
-
4x0=0, and no keeping, therefore it's 0 on the bottom line. Hence the upper line is 1. Pic
-
Notice that it has come back to 1. It's easy now. So you find out the number is ...271002710027100...00271. Do whatever you want to find out the answer. Use a calculator, or prove anything. I used a calculator and count the number for my dinner's sake.
I just used long division to see if there is a pattern and found that 4 1 × 2 7 1 = 1 1 1 1 1 .
Your first solution I guess?
I also came to have a look at his very first solution.
Every time 5 ones come together the number is divisible by 41!!!
Why???
Log in to reply
i did as follows...start with 111 and start doing long division by 41 if you get a remainder then put another "1" with the dividend...keep doing this till your remainder becomes zero...you will see the remainder becomes 0 after 5 ones this method will work as long as the number of ones remain small, after which it will get tedious.
Log in to reply
Thanks Sahil.......yours was a great approach....
I checked it on the calculator actually...just try it ...11111/41 gives you no remainder so now if u have 5,10,15....ones together the number will be divisible by 41
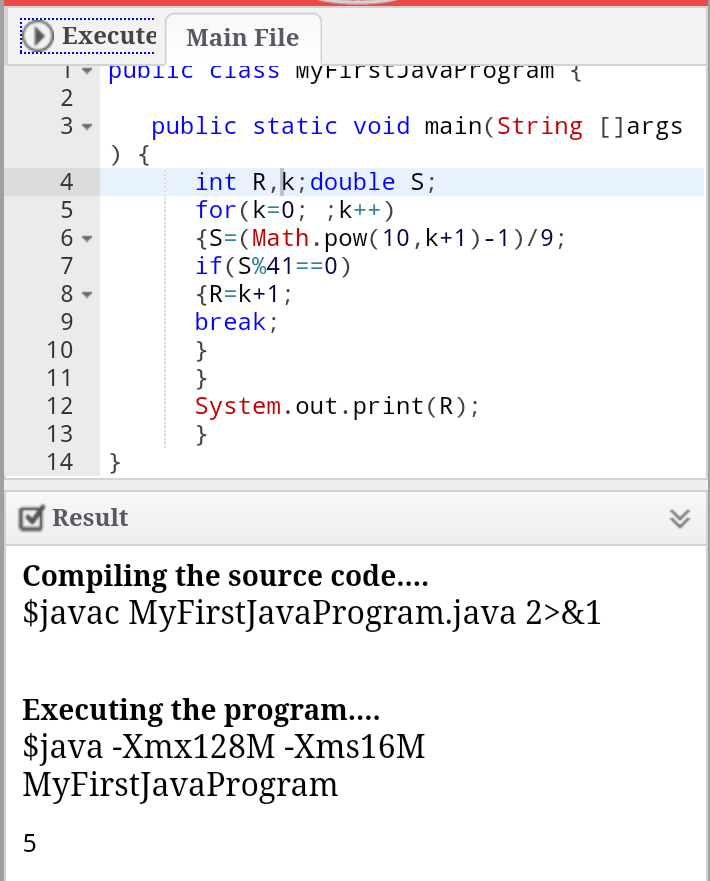 A JAVA code is all you need
A JAVA code is all you need
Here is another solution 1111111111/41=27100271 .Therefore answer. also can be 10
11..1(n times) is divisible by 41=>41| 99..9(n times).now 99..9=(10)^n-1. now order of 10 modulo 41 must divide n which is 5
when we take that n 1's are divisible by 41 then by checking we get that after every five number a integer as a result , than n must be factor of five.
The smallest number is 11111 in which n=5 so the largest factor of 5 is 5 itself
1111.......upto n mod 41 n must be of the form 40k where k is any natural number 40 = 2^3*5 Therefore, 5 is the largest integer
It isn't very elegant, but just doing 11/41, 111/41,... you get 11111/41 = 5