Dizzy on a circular path!

Generalizing:-
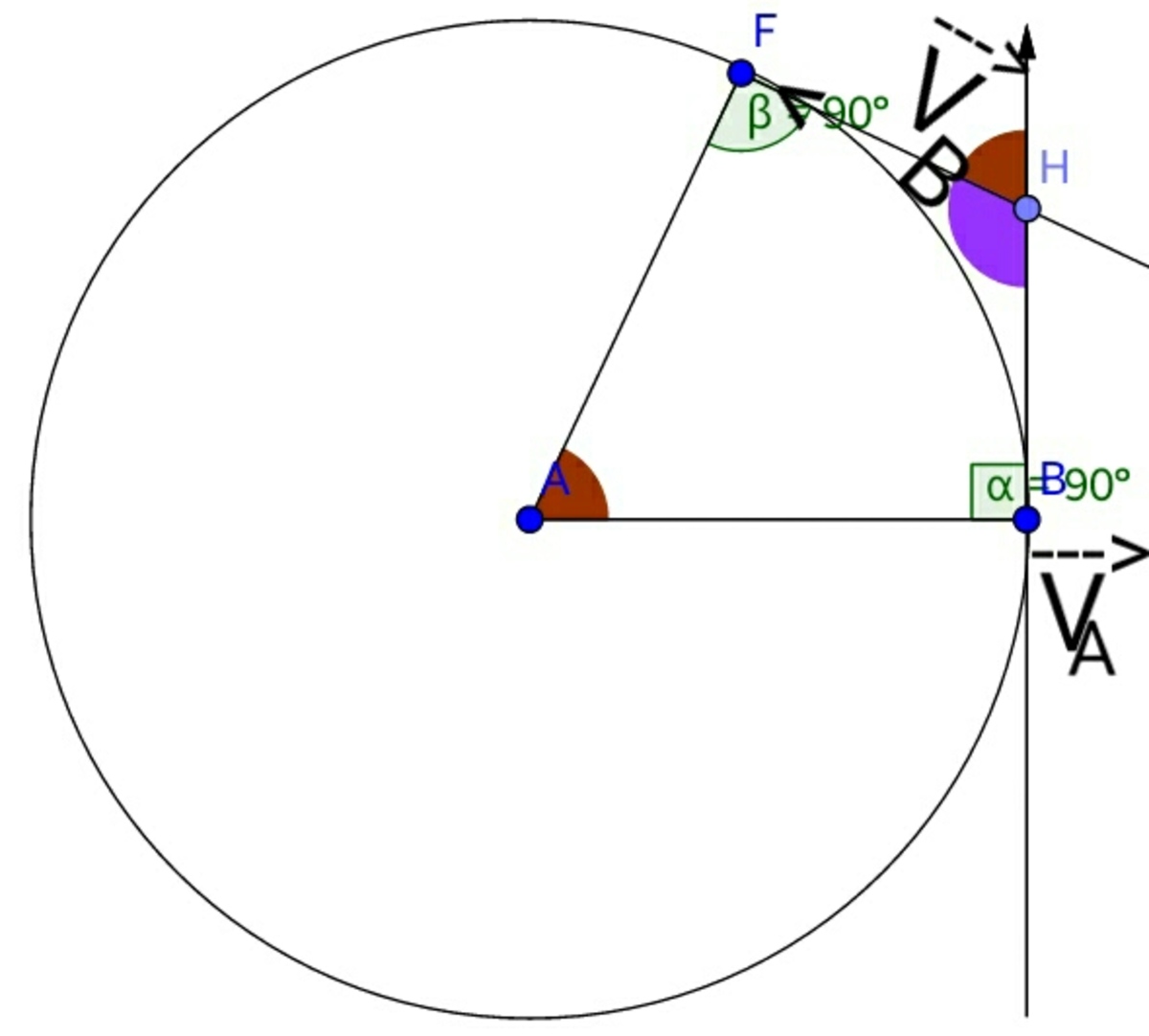The red angle is theta.

Let the speed be $s$ and angle be $\theta$ .
Now velocity has speed and direction, so:-
$\begin{aligned} \triangle{V} & = \vec{V_B} - \vec{V_A}\\ & = \vec{V_B} + \left(-\vec{V_A}\right) \longrightarrow \boxed{1} \end{aligned}$

Now, the vectors can be redrawn as the following:-

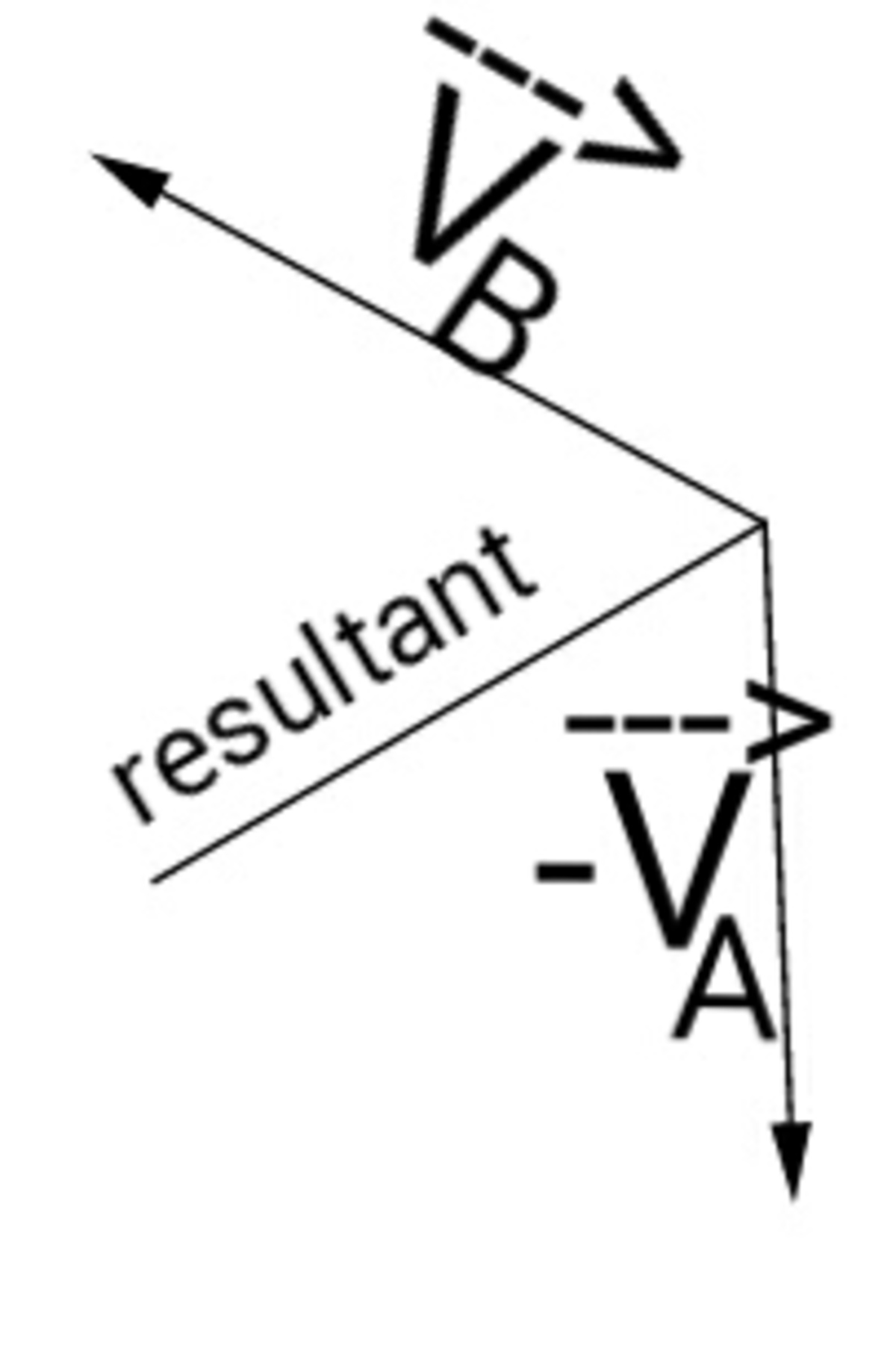
But we dont know the angle between the vectors. So, observe in the first figure that $\angle{\text{FHB}} = 180 - \theta$ anditis the angle between the vectors we want.

So, taking the value in $\boxed{1}$ we get:-
$\begin{aligned} \triangle{V} & = \sqrt{s^2 + s^2 - 2×s×s×\cos\left(\theta\right)}\\ & = \sqrt{2s^2\left(1 - \cos\theta\right)} \longrightarrow \boxed{2}\\ \\ \cos2\theta & = 1 - 2{\sin}^2\theta\\ \cos\left(\dfrac{2\theta}{2}\right)& = 1 - 2{\sin}^2\left(\dfrac{\theta}{2}\right)\\ \cos\theta & = 1 - 2{\sin}^2\left(\dfrac{\theta}{2}\right)\\ 2{\sin}^2\left(\dfrac{\theta}{2}\right) & = 1 - \cos\theta \longrightarrow \boxed{3}\\ \\ \text{Substituting} \ \boxed{3} \ \text{in} \ \boxed{2}, \ \text{we get}:-\\ \\ \triangle{V} & = \sqrt{2s^2 × 2{\sin}^2\left(\dfrac{\theta}{2}\right)}\\ & = \color{#20A900}{\boxed{2s\sin\left(\dfrac{\theta}{2}\right)}} \end{aligned}$

So, in this question, we have $s = 150$ and $\theta = 120$
So, $\begin{aligned} \triangle{V} & = 2×150×\sin\left(\dfrac{120}{2}\right)\\ & = 300 × \sin 60\\ & = 300 × \dfrac{\sqrt{3}}{2}\\ & = 150\sqrt{3}\\ & = 259.807\\ & \approx \color{#3D99F6}{\boxed{260}} \end{aligned}$

v^2+v^2-2v v cos(120) gives the answer... Simple geometry