Dlanod's adventures, the End

Geometry Level 4

As it often happens in the life of a cunning real estate developer, Mr. Dlanod's plans have changed once again. He is now planning to build on a grander scale: Ten hotels in the wilderness (complete with casinos and golf courses), at the points $(x,y)$ with $x=0,6,12,18,24$ and $y=0,6$ , where distances are measured in kilometers. A network of roads needs to be built so that any hotel is connected to any other, but the budget now allows for at most 50 km of roads.

Can the task be accomplished?

This is a sequel to this problem .

No They are working on finding out Yes

2 solutions

Mark Hennings
Nov 15, 2018

This paper summaizes the results for this class of problem. If we are trying to find a minimal Steiner tree for an $m \times 2$ array of equally spaced points (the paper calls this a "ladder"), then the length of the minimal Steiner tree is $\sqrt{\Big[m\left(1 + \tfrac12\sqrt{3}\right) - 1\Big]^2 + \tfrac14}$ when $m$ is odd (the paper gives a formula for even $m$ as well), if the distance between adjacent points is $1$ . In this case, this means that the length of a minimal Steiner tree is $6\sqrt{\Big[5\left(1 + \tfrac12\sqrt{3}\right) - 1\Big]^2 + \tfrac14} \; = \; 6\sqrt{35 + 20\sqrt{3}} \; = \; 50.07071581$ kilometres. This means that the task is impossible.

Exactly! Dlanod cannot afford those extra 70 meters, and the project will be scrapped.

Otto Bretscher - 2 years, 6 months ago

Is it possible to get a picture of the roads network that illustrates this result ? Trying to play with the Steiner points, I couldn't get less than 51.67 km... Thanks Gérard

Gerard Boileau - 2 years, 6 months ago

You find a picture here , on page 195, the one labelled $n=5, b=1$ .

Otto Bretscher - 2 years, 6 months ago

@Otto Bretscher – Very interesting. Thank you for sharing this problem and the reference paper !

Gerard Boileau - 2 years, 6 months ago

@Gerard Boileau – I was introduced to this topic by the great magician Persi Diaconis some 30 years ago as we were teaching Linear Algebra together at Harvard (with Persi being the very senior colleague, of course). Rather than writing the next problem set or exam together at our weekly lunches (which he left to me), he was always eager to show me some "interesting maths," and many Harvard Faculty Club napkins were wasted on Steiner trees (or, rather, put to good use).

I'm glad to have found a forum at Brilliant to share this fun stuff, and I want to thank you for your continuing interest, Gérard.

Otto Bretscher - 2 years, 6 months ago

@Otto Bretscher – Nice story, indeed ! :-) I retired one year ago, and enjoy this new period of my life as maths hobbyist, what my sons definitely do not understand ! I appreciate having such an opportunity of having pleasant conversations with nice people...

Gerard Boileau - 2 years, 6 months ago

@Gerard Boileau – I plan to retire next year, and Brilliant will be one of my ways to keep the mind active... Enjoy!

Otto Bretscher - 2 years, 6 months ago

Otto bretscher sir can you tell me about some more such interesting stuff

Mr. India - 2 years, 6 months ago

But of course; I'm always interesting in hearing about interesting stuff.

Otto Bretscher - 2 years, 6 months ago

David Entwistle
Nov 24, 2018

Nice problem. I think my numerical solution arrives at the right general arrangement, but not quite the minimal solution. I arrived at 50.78 km.

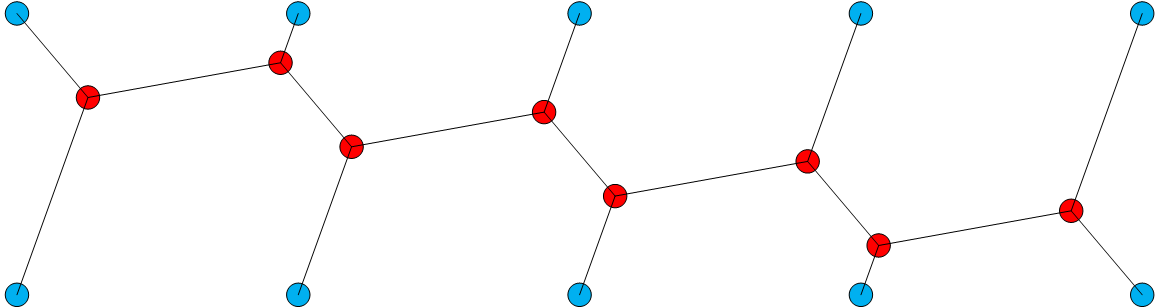
Thank you for sharing this intriguing design!

Actually, the Steiner minimal tree has more of an alternating pattern of "columns," as you can see here on Page 195, the tree labeled $n=5,b=1$ . Your design is their tree $n=5,b=0$ . (They work with a distance of 2 km between the vertices.)

The length in the case of the $b=0$ design comes out to be 50.78 km, so, your numerical approximation is very good indeed.

Otto Bretscher - 2 years, 6 months ago

Ah, thanks - I see my original mistake now.

Now I get 50.07 km.

David Entwistle - 2 years, 6 months ago

Beautiful! Thank you!

Otto Bretscher - 2 years, 6 months ago

Dlanod's adventures, the End

2 solutions

0 pending reports