Does this needs construction?
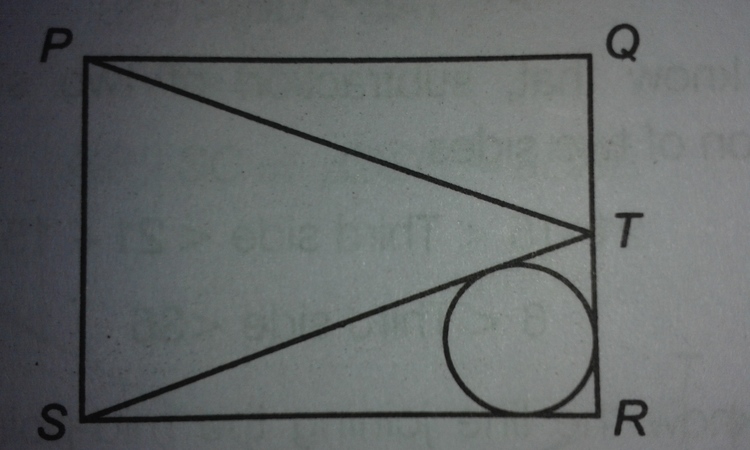 P
Q
R
S
is a square of side 6 cm each and
T
is a mid-point of
Q
R
. What is the radius of circle inscribed in triangle
T
S
R
?
P
Q
R
S
is a square of side 6 cm each and
T
is a mid-point of
Q
R
. What is the radius of circle inscribed in triangle
T
S
R
?
The answer is 1.1458.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Sir, i solved using quadratic equation and giving two positive solutions why is this so ?
Log in to reply
What was your quadratic equation? Perhaps the second solution is the radius of the circumcircle.
Log in to reply
now i get it since other solution is about 7 which is not possible in right triangle with hypotenuse is 6 !!!
@Abhay Kumar I think that you meant triangle TSR, as TQR is a side of the square. :)
1.5 (3 - 5 ) = 1.145898033750315455386239496903+
Just the same way.
Name the points where the circle touches QR as U, where the circle touches SR as V and where the circle touches ST as W. Clearly as TR=3 so UT=3-r (r is the radius of the circle which we need to find). So, TW=3-r( TW and TU are tangents from an external point T). Also, VR=r so VS=WS=6-r. This means that TS=3-r+6-r=9-2r. But TR=3√5 by Pythagoras Theorem in ∆TRS. So, 9-2r=3√5, which means r=1.146cm
same way buddy u think a lot like me
Log in to reply
Maybe You can upvote my solution then?
You look right, but if we square you last equation and then solve for R there are actually two positive values. Can you explain me why and which one to choose ?
Log in to reply
What are the two values you are getting?
Log in to reply
Ok. I Got it. One value is the answer and the other is 7.85 which is not possible as the longest side is 6 cm itself.
Log in to reply
@Vishal Yadav – Yes Exactly and what was the need to square a linear equation?
In any rt. triangle ABC where /_B=90°, in-radius = (AB+BC -AC)/2. In this case, r=(6+2 -√45)/2~1.1459 cm

The formula we can apply here is r = s A , where r is the radius of the incircle of a given triangle and A , s are respectively the area and the semi-perimeter of the triangle. A proof of this formula is given here .
In this case, Δ T S R is a right triangle with side lengths ∣ T R ∣ = 3 cm and ∣ S R ∣ = 6 cm, giving us an area of A = 2 1 ∗ 3 ∗ 6 = 9 sq. cm.. Since the hypotenuse S T has length 3 2 + 6 2 = 4 5 = 3 5 cm., the semi-perimeter is then s = 2 1 ( 9 + 3 5 ) cm..
Thus we find that r = s A = 9 + 3 5 9 ∗ 2 = 2 3 ( 3 − 5 ) = 1 . 1 4 6 cm. to 3 decimal places.