Dodecahedron Space Station
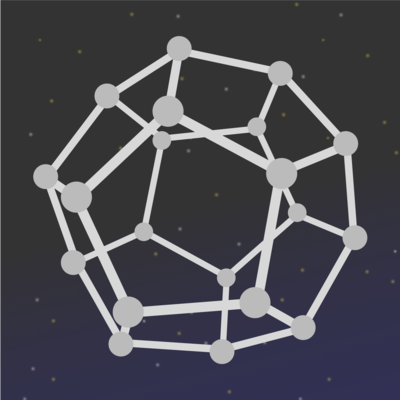
You're on Space Station Dodecahedron (shaped exactly like a regular dodecahedron), where each vertex is a research node, and the edges are tubes which connect the nodes.
To fix a critical failure in life support systems, you must travel by connecting tubes, visiting each node of the space station exactly once, and then return to your starting node.
Is this possible?
Hint : The vertex graph of a dodecahedron is provided below.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
11 solutions
contradictory question. ONLY "ONCE" then RETURN to the original node..... You are now at the original node TWICE. Hmmmmmm
Log in to reply
You count up the "once"s before returning. After you're done "visiting each node of the space station exactly once," then you stop counting and THEN return. ;-)
Log in to reply
That's the correct interpretation, and it makes the solution very easy (but it is probably not intended that way).
Log in to reply
@A Former Brilliant Member – Except that is exactly what it says, so it would be logical that it was intended.
GRAPH METHOD we can straight forward put the concept of 'eularian bridges' according to which in a graph if we call travel all the edges only once and come back to the starting point if and only if the no. of odd nodes is even. odd nodes-a node connected to odd no. of edges
Log in to reply
I've made this exact mistake myself... The thing is that in this problem we don't need to travel all EDGES only once, we just need to visit all nodes.
Also, you're not stating the condition correctly. There is an eulerian cycle (that comes back to the starting point) iff the number of odd nodes is ZERO. There is an eulerian path (that doesn't necessarily come back to the starting point) iff the number of odd nodes is at most two. (And FWIW in absolutely any graph, by the fact that each edge connects two nodes, there will always be an even number of odd nodes.)
I think you are mistaking the eulerian path with the hamiltonian path . The eulerian path is the problem of visiting every edge and is as easy as you described to compute. The hamiltonian path is the problem of visiting every node and is actually NP-complete.
thanks for correcting me i didn't know about hamiltonian paths so thanks
"Here they are"
Isn't this the "Hamiltonian cycle" problem, since you are required to return to the initial node?
Here is one possible path:
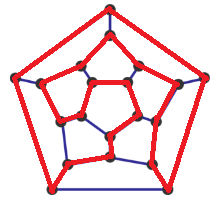
Ohhhh each NODE once, ignoring vertices.
I continue to fail to read the questions right.
Log in to reply
Jajaja it also happens to me usually
The nodes are the vertices...
I thought I was supposed to connect the nodes with the tubes as well, so that would be impossible.
Does it matter where the start is?)
Very professional. I love it!
voted for art :)
It's important to note that Hamilton path exists iff there's even (except 0) number of vertices that has odd number of edges connected to them.
In this problem all 20 vertices are odd edged. 20 is even, that means path exists.
This is the only answer using a theorem and not relying on other concepts. Great answer.
Brilliant Answer. It doesn't rely on brute force or esoteric facts. The only rule used applies to ALL networks.
This answer is incorrect. Try making a graph which does not follow this rule, where there's an odd number of vertices with an odd number of edges connected to them.
Log in to reply
Hint: It's impossible. Any edge will connect to 2 vertices, hence summing the number of edges connected to each vertex will always yield an even number. If there were an odd number of vertices with an odd number of edges connected to them, this sum would be odd, which isn't possible.
The dodecahedron may be observed in the vertex graph as three concentric "rings". Starting from any node in either the center "ring" or outer "ring", the "ring" is traversed until the last node of the "ring" is reached, thus completing the "circumference", and then the traveler moves to the next ring. In this manner, all nodes may be visited only once.
But you have to end at starting position.
Log in to reply
agreed. I missed the requirement that you must end where you begin!
A Hamiltonian path exists if every node has an even number of edges or if an even number of nodes has odd number of edges. The dodecahedron satisfies this condition... so it's possible.
Correct me if my intuition here is incorrect but this problem is similar to the Bridges of Königsberg problem and thus Euler's solution to that problem applies to this one. But kudos are due to those who mapped a solution.
This is a variation of the Hamiltonian Path Problem. The original one has no start or finishing points. However, this adds a twist to it as you must determine that one exists with a specific point as starting and finishing point.
THE VARIATION IS CALLED A HAMILTONIAN CYCLE
Use the coloring principle
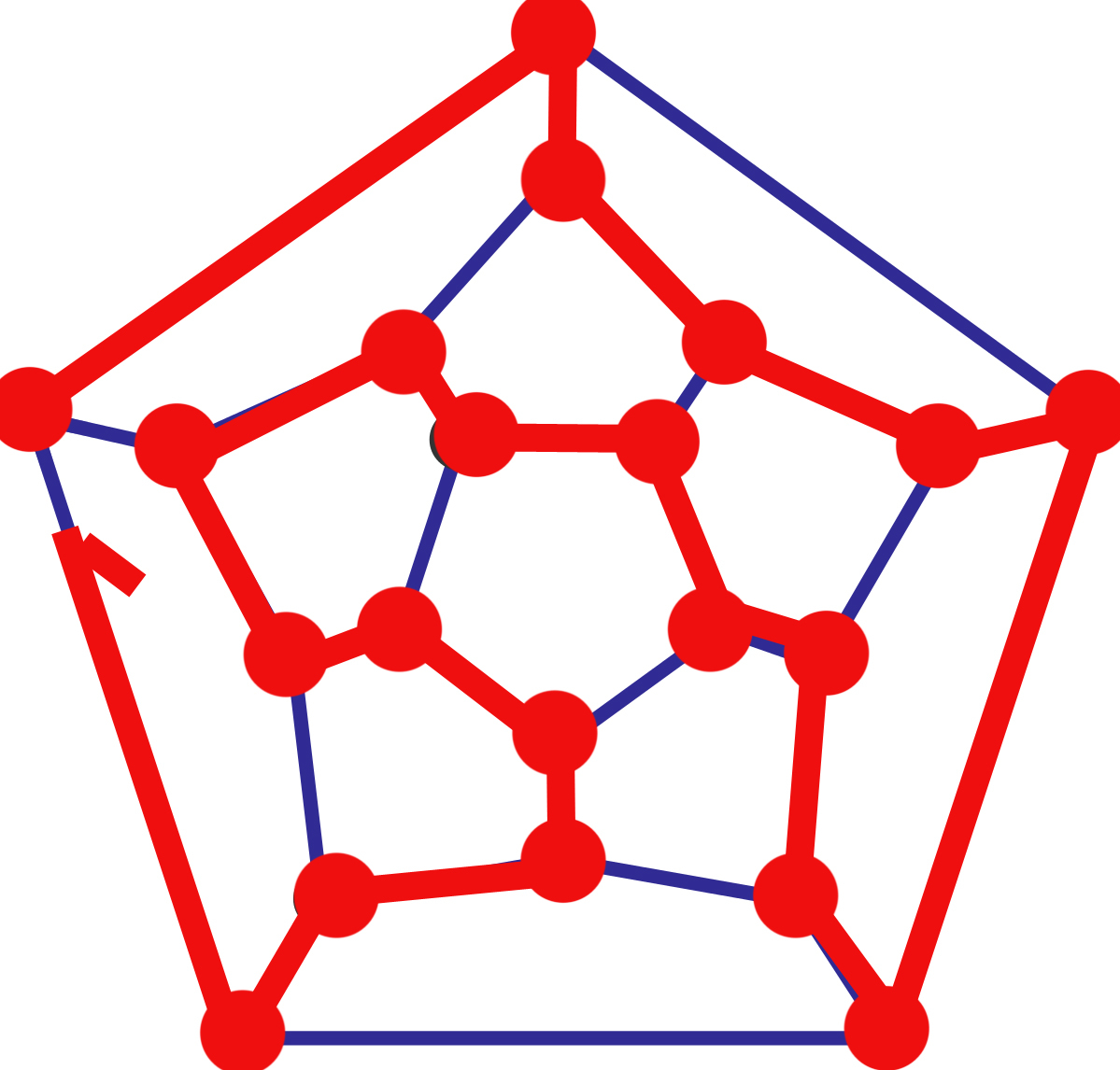
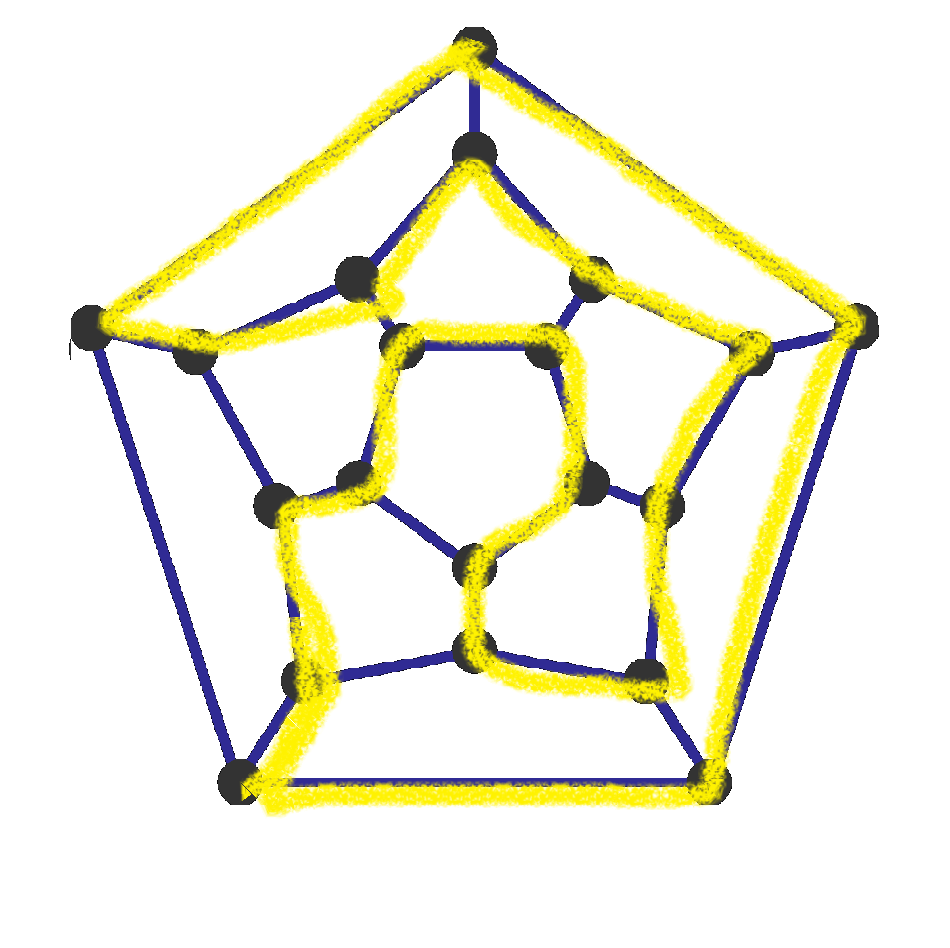
This problem is asking if there is a Hamiltonian path on a dodecahedron. We know that every platonic solid has a Hamiltonian path. Here they are: