Does the couch fit through the door?
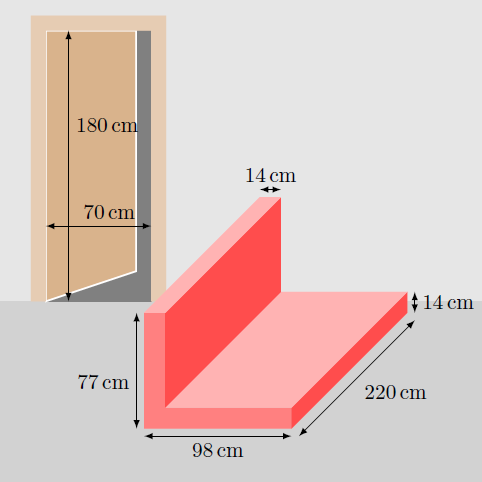
Peter has ordered a new couch for his TV room, which has a rectangular L-shape as a cross-section. The piece of furniture is 220 cm long, 98 cm wide, and 77 cm high. In addition, the padding has a thickness of 14 cm.
Now Peter notices that the opening of his room door is only 70 cm wide and 180 cm high.
Does the couch still fit through the door anyway?
Assumptions: The couch can be rotated arbitrarily. It fits through the door if its cross-section lies completely in the rectangle of the door frame. Additional wiggle room is not necessary.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Take the door off first, unless there is no wall on the left side
Log in to reply
Peter will probably have to remove the door leaf for the couch to fit through, since we considered only the door frame.
Nevertheless, I would not recommend buying furniture that fits EXACTLY through your door
Log in to reply
When I came up with the figure of 70, I got so excited that I hit the "discuss solution" button instead of the "submit" button. Ahh, that happens... anyway, yes, I've had plenty of experience with trying to get stuff through doorways, and taking doors off has almost become routine because for some reason, it's always the last couple of inches that count.
I liked your method of solving this one, very unusual.
Log in to reply
@Michael Mendrin – The points that can be collected here through correct answers are not the actual motivation for me. If a problem or an idea changes the way you see the things, then it's definitely worth it.
If someone asks me the question, what linear algebra is useful for in everyday life, then at least I have an answer. (Although a purely geometric solution would probably be easier)
The couch can fit if the L-shaped cross-section is rotated parallel to the wall with the door and then tipped diagonally, as shown:
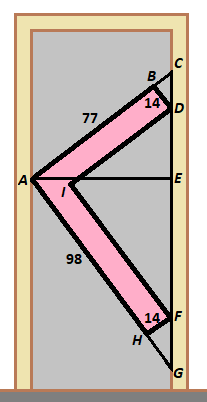
If the sides of the couch are extended as in the diagram, then there are several similar right triangles we can use in our calculations to show that it will fit through the door.
Since I D = 7 7 − 1 4 = 6 3 , I F = 9 8 − 1 4 = 8 4 , B D = 1 4 , F H = 1 4 , and △ I D F ∼ △ B C D ∼ △ H F G , B C = 1 4 ⋅ 8 4 6 3 = 2 2 1 and H G = 1 4 ⋅ 6 3 8 4 = 3 5 6 .
This means A C = 7 7 + 2 2 1 = 2 1 7 5 and A G = 9 8 + 3 5 6 = 3 3 5 0 . By Pythagorean's Theorem on △ A C G , C G = ( 2 1 7 5 ) 2 + ( 3 3 5 0 ) 2 = 6 8 7 5 . (Since this is less than the door's height of 1 8 0 , we know that this orientation of the couch will fit through the door by height.)
Finally, since △ A C E ∼ △ A C G , A E = 3 3 5 0 ⋅ 6 8 7 5 2 1 7 5 = 7 0 , and we know that this orientation of the couch will also fit (just barely) through the door by width.
Since the coach is longer than the height of the room door, you can not just get upright through the door. Instead, the coach has to fit through the door frame with its entire cross section of the L-shape. Therefore, we consider only the two-dimensional problem definition, whether the L-shape fits properly turned into the rectangular area of the door cross-section.
The cross section of the coach is a polygon A B C D E F . We consider the line g , which goes through the two points C and E . This line has a distance d to the point A . So if d ≤ 7 0 , then the coach fits through the door frame.
We put the point A in the origin of our coordinate system. The line g is then spanned by the two position vectors C = ( 9 8 , 1 4 ) and E = ( 1 4 , 7 7 ) . This results in a straight line equation g = { C + λ ⋅ V ∣ λ ∈ R } with the difference vector V = E − C = ( − 8 4 , 6 3 ) , which is parallel to g . The distance to point A corresponds to the minimum length of all position vectors in g . This minimum is determined by setting the derivative after the parameter λ to zero: ⇒ ⇒ ⇒ d 0 λ d = λ ∈ R min ∣ C + λ ⋅ V ∣ = d λ d ∣ C + λ ⋅ V ∣ = 2 ∣ C + λ ⋅ V ∣ d λ d ( C + λ ⋅ V 2 ) = 2 ∣ C + λ ⋅ V ∣ d λ d ( C 2 + λ 2 ⋅ V 2 + 2 λ ⋅ C ⋅ V ) = ∣ C + λ ⋅ V ∣ λ ⋅ V 2 + C ⋅ V = − V 2 C ⋅ V = − ( − 8 4 6 3 ) ⋅ ( − 8 4 6 3 ) ( 9 8 1 4 ) ⋅ ( − 8 4 6 3 ) = − 1 1 0 2 5 − 7 3 5 0 = 3 2 = ∣ ∣ ∣ ∣ C + 3 2 ⋅ V ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ( 9 8 1 4 ) + 3 2 ⋅ ( − 8 4 6 3 ) ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ( 4 2 5 6 ) ∣ ∣ ∣ ∣ = 4 2 2 + 5 6 2 = 7 0 Thus, the couch fits from the width exactly through the door.
As a second condition you would have to check if the height fits. However, this is not a problem since the diagonal of the L-shape has the length 9 8 2 + 7 7 2 ≈ 1 2 5 and is therefore much smaller than the door height.
The solution is illustrated here graphically: