Domino waves
Two identical rows of 1 0 0 0 dominoes are initiated in two different ways:
- In row A, the first domino is barely tipped over, and hits the second domino in 1 s .
- In row B, the first domino is pushed so that it hits the second domino in 0 . b a r 3 3 s .
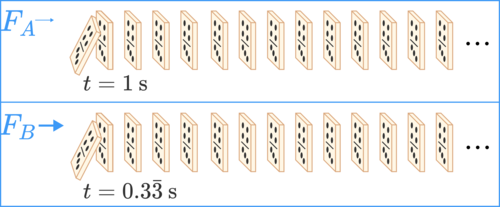
How long will the two rows take to finish falling?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
13 solutions
What about conservation of momentum ? Assuming we have ideal conditions, the gravity is in vertical direction and if we just consider the horizontal direction, the CoM of the first domino moved 1/3 times faster and will stop giving its total momentum to the next domino.
Log in to reply
The momentum of the system is negligible because all the dominos are not moving simultaneously. In the end, they will be lying at their original positions and hence the center of mass has not moved at all or very little.
I didn't get it. The initial push of the second was 3 times faster than the first, so it means the momentum it has is 3 times as much, and assuming no energy is lost, momentum will still be conserved. And yes the G.P.E is the same in both, but there is more energy in the second case which is 3 times as that if the first...
I must be missing a point, but I don't seem to get why the initial push would somehow be negligible..
Log in to reply
The momentum is not conserved due to the friction of the table
Log in to reply
The momentum of a single domino is not conserved because it is hitting with the others and the momentum of all the dominoes as a system is itself very small and obviously not conserved as at the end the dominoes will be at rest on the ground.
Regardless of the idea that each domino will fall at the same rate due to gravity, row B will finish first because it has a head start. It starts 2/3 of a second earlier and will retain that advantage throughout the simulation.
Haha. If we can claim that the initial force becomes negligible, then we can pass every physics problem. Without doing any math! Useless questions with pathetic answers often cause me to leave this poorly managed website for a couple months. It's not brilliant, it's just a hack job. Hopefully this time I'll remember how annoying it is and never comee back. Unsubscribe me!
Log in to reply
Think about the fact that velocity is a vector. At the time the domino's touch in row B, some of the horizontal momentum of the initial domino has been converted into vertical (downward) momentum. This means that each subsequent domino in row B will receive a fraction less horizontal force than the previous to the point that the initial horizontal velocity becomes negligible.
Log in to reply
Nonsense. Momentum does NOT convert into momentum in other directions. Momentum is a vector quantity, of which projection onto any plane or axis is conserved in the absence of external forces.
Log in to reply
@Manuel Ruiz – With the assumption that the dominos does not slide along the ground they make a rotational movement around their back base edge (as they are tipping over), at the impact of one domino to the other, the new domino can only move in a direction perpendicular to the axis of their back base edge, right? So all the momentum from the previous domino (at the moment of impact) that can not be represented by a component vector in a direction perpendicular to the new dominos back base edge cannot move that new domino, and is then lost, No?
I think the conversion Daniel was talking about was the behaviour of rotational momentum as observed by other vectors in a fixed grid? I don't know.
Log in to reply
@Gustaf Carstam – The vertical component is indeed "lost" due to contact force. But it's not like the momentum vector would be rotating with constant length or something. The vertical story is completely indepent from the horizontal story.
If you think the answer is wrong, then why don't you post your own answer, preferably with lots of math. Please enlighten us.
Agree. This kind of problem with limited choices, often in radio button UI, is really annoying. Some sort of a trap. And they removed the 'Relevant Wiki' link in Problems of the Week for some unknown reasons.
If you read the option correctly then the answer actually is 100 percent correct. The option says 'Row A and Row B take "about the same time" to finish'. See that? There was nothing wrong. This place teaches this one very important thing. Always read the statements properly. There are a lot more examples that I can give you. Even when you study the courses you can understand how crucial it is to pay attention. When I solve problems and have doubts then I look back and read the course again. After reading it word by word again I am able to point out the parts where I didn't pay attention but which turned out to be important. Because of that now I am way more focused while reading 'and explaining' anything to anyone and that is one of the most crucial parts one needs to learn to study science. So next time you think some question or explanation in wrong and that this platform isn't good, think ten times before posting stuff like this. Ignorance like this is the reason why people like you leave this platform sooner or later.
While the force on the initial domino B is 3 times the force on the initial domino A, the dominoes within each chain are not touching, so the force on each domino in chain B does not remain at triple the force on chain A. They will finish at just about the same time. Try this out for yourself!
Would not a more agressive initiation of the first domino cause it to impart more force upon the second, though, regardless of initial contact?
Log in to reply
That’s what I thought Certainly a faster moving domino would also cause the subsequent domino to move faster as well
Log in to reply
The effect of the initial force would be negated within a few Domino’s as the system normalises to an F=Mg model - given the 1000 domino criteria the expected result would be for the 2 chains to fall at the same speed with one slightly behind the other.
Log in to reply
@Trev Lahy – Please show mathematically (other than simply stating F=mg (which should be F=ma in this case)) why the system would 'normalize'.
Log in to reply
@Jesse Otis – The answer is friction. Without friction, all dominoes in row B would have a higher energy than the corresponding dominoes in row A. However, in that case, the energy of the last domino in both rows would be dominated by the potential energy of the 999 dominoes before, and not the initial push. As velocity scales as the square root of energy, the speed will be very similar.
In practice, due to friction, both rows will ultimately fall at exactly the same speed. However, row B will remain slightly ahead of row A. Not just by 0.6666... seconds, as the second and third (etc.) dominoes will also fall at slightly higher speed. But probably more like 1 second sooner. Over all 1000 that 1 second is negligible. 1000 dominoes probably takes over 1 minute.
Not a fan of this problem, it seems to me since the first and second B dominos touch 2/3 faster than the first and second A domino's they would all finish falling first.
Assuming the dominoes have the same mass, the initial domino in B has a higher velocity and more momentum. This higher momentum would be transferred to the second domino, and so on.
Also, there is insufficient information to know if the initial domino in A would even cause the second domino in A to fall.
Log in to reply
Even if the dominoes are started by gently placing the first one diagonally against the second one, as shown in the image, the whole row will fall. The first domino pushes the second domino towards the right, and due to friction, the second one will fall over instead of remaining vertical. You can place dominoes diagonally in a stable manner against a block of dominoes without separation.
If the kinect energy is converted to potentional, the force that a dominoes in the roll B would hit other wouldnt be 3 times that in the roll A? Within that, the colum B would take 1/3 of the Colum A time to fall everything.
Log in to reply
Why would/could you convert kinetic energy to potential energy?
Log in to reply
Because of conservation of energy? When you throw a ball to a level roof, the kinetic energy required for the ball to reach there will be converted into the potential energy it will have to fall back down...
This is technically the wrong answer. It doesn't explain why the two rows finish in about the same time.The answer right below this is the correct explanation.
Run a mental simulation or write a code in python with the mechanics of dominoes falling, you will see that whilst B gets a minuscule head-start they both equalize exponentially since the initial force doesn't translate to every domino tile equally. So whilst there is there that row B will finish by a 0.66 secs faster, it will never finish 2/3 or 1/3 of the time A finishes, so the logical conclusion is to answer the one option that comes closest to the prediction and eliminate those who are off by a large margin, so we are left with the answer of A and B finishing in "about the same" time. (note the key word "about" and not not necessarily "the same")
I've been learning Python for almost a year now and even I can't figure out how you can possibly write such a code...
'Whilst.' I've never said whilst. I've gotta toss that in at a Sales meeting. That'll shake 'em up.
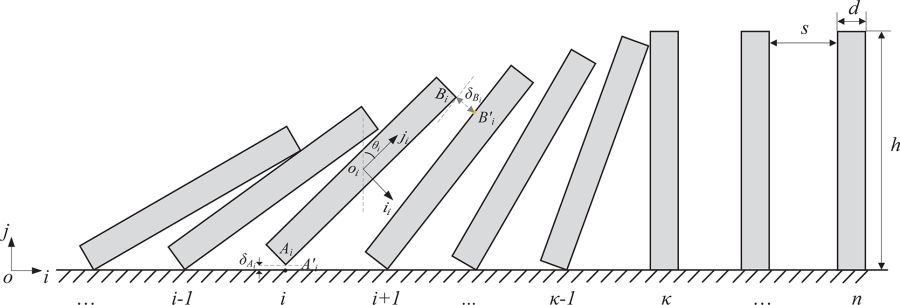
If the dominos were evenly spaced in an exactly straight row in gravity-free space, and if you strike the first one with some velocity v , thus imparting the system with a certain amount of energy E , then by Conservation of Energy, the system will only contain constant energy E throughout, and so at the end of the row of domino, the last one will fly off with the same velocity v . The faster v is, the faster the "wave" will get to the other end. It might seem that, therefore, F B would finish quicker.
However, on the ground with gravity, we have to consider the gravitational potential energy of falling dominos, and it's not necessarily a fact that all of the energy of one falling domino is transferred to the next. After all, one domino could miss the next. But assuming that the wave is asymptotically moving forward with constant speed, if the instantaneous velocity of the tip of one standing domino just struck by the previous one is v , then it's the same for the next standing one when struck. Given ( v , h , d , s , g ) , or standing tip velocity, height of domino, thickness of domino, space between dominos, and gravitational constant, one can compute the tip velocity of one falling domino at the moment of its impact on the next standing domino, which determines its standing tip velocity, which is the same v . Solving for v in terms of ( h , d , s , g ) involves elliptic integrals, but regardless of the exact answer, the initial velocity at the start doesn't have a bearing on this long term asymptotic wave speed. Regardless of how the first domino is struck, the long term wave speed of falling dominos depends only on the dimensions and spacing of the dominos and gravitational constant.
Striking the first domino such its initial instantaneous tip speed is less than the asymptotic wave speed can be replicated by having a few more dominos before the first one, such that the "new first one" is barely tipped over, so that F B becomes like F A in the long run, which is why "Row A and Row B take about the same amount of time to finish falling".
I made an analogy with air drag. It seemed obvious to me that the "wave" would tend to reach certain terminal velocity because of the ever more frequent collisions of dominos. So, eventually both rows would've had the same velocities. Naturally, the one with initial speed would've required less time than the other, but not even close to 1/3 or 2/3 of the time of row A.
I'm just wondering how valid this reasoning is?
The force of the first domino doesen't really have a measurable impact on the entire system thus If you consider the first domino to be the trigger for starting a system of 999 dominos the main diffrence between row A and B finishing is likely to be around 0.66 seconds.
An easier way to think of this is that while Force B is greater and takes less time to push the first domino, the speed at which the dominoes fall is a wave and equivalent to the speed of the wave propagation through the system since each domino isn't touching at t=0.
Brilliant! Since nothing is said about spacing between dominoes, why not stick them together and claim they're all falling with the speed of sound!
Great concept!!
Since there are 1000 domino's in each row, it doesn't really matter how strong the first domino is pushed. In the end they are all pushed down (or falling) by gravity with always the same force. Pushing the first stone is only necessary to introduce the chain reaction. For example starting a fire with a high powered laser or a classical lighter has no influence on how long it takes to burn an haystack, as long it was hot enough to get the process started.
Let n = the number of dominos, m = mass of each domino.
Kinetic energy gained in each falling domino equals to its loss in potential energy. K E t o t a l = K E i n i t i a l + n P E
Using K E = 0 . 5 m v 2 , the speed at which all the dominos fall is:
v = n m 2 K E t o t a l = n m 2 ( K E i n i t i a l + n P E ) = n m 2 K E i n i t i a l + m 2 P E
As n increases to a large number, the inital KE term decreases and the PE term dominates.
1000 is pretty large, so it is reasonable to assume that the two rows fall at the same speed, and hence about the same time.
How does the spacing between the dominos affect v ? Wave speed of falling dominos isn't a constant for all spacing.
How is it that you find the kinetic energy term diluting out (you have it divided by n )? After each domino falls and settles, it has no remaining kinetic energy. So it has to have all gone into the next domino (or... someplace else).
Log in to reply
And what if the first domino was hit with a high velocity rifle bullet of the same effective mass of the domino, and assuming all the dominos are hinged to the ground so they don't flying in all directions? What then happens to the kinetic energy of the first domino imparted by the bullet? Will the long term wave speed still be the same, considerably slower than the first domino? Okay, better have 10,000 or 100,000 dominos for this one.
violets are blue, roses are red, from the second domino speed remain the same till the end.
If we look at the system's center of mass for both cases we can assume that the initial and final statements are the same for both rows. Since there's only horizonal velocity at the beginning, the time of the free falling depends only on the gravity acceleration , which is the same for them both. Thus the time from initial to final situation is the same.
Row A starts with V1, Row B starts with V2.
V1 < V2.
The dominos take T time and, and have a constant and identical acceleration A.
So as time progresses:
The speed of Row A, becomes: Va = V1 + A•T
And the speed of Row B, becomes: Vb = V2 + A•T
As T goes to infinity, T→∞, the speeds become identical:
Va = 0 + A•T = Vb
Additionally, any distance D made between the two rows, will become insignificant as well as T→ ∞:
Xb = V2•T + ½AT²
Xa = D + Xb = D + V2•T + ½AT²
T→∞:
Xb = 0 + ½AT² = ½AT²
Xa = 0 + Xb = 0 + 0 + ½AT² = ½AT² = Xb
What is the meaning of this conclusion? The meaning is that, the distance passed by both rows with respect to time, will become closer and closer to each other(in terms of ratio).
Based on life experience, it seems that the speed of domino is the same.
Let's consider the energy in two rows.
Besides the initial push, the kinetic energy in two rows are all coming from the gravitational potential energy of the dominoes when they are falling down. The different work done by the two initial push will be transferred to the later dominoes with some certain fraction in each collision. And after a great amount of dominoes, this part of energy will become negligible. The gravitational potential energy, which are the same in two rows, will be the main cause of the motion of, say, the 1000th domino.
Therefore, we can estimate that the time taken for two rows to fall down will be approximately the same.