Related to open problem #1: Don't fight each other
Logic
Level
2
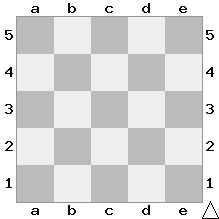
What is the maximum number of bishops you can place on this chessboard such that none of them can attack each other in one move?
7
8
4
5
6
9
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
8 bishops is maximum.
We have shown that 8 can be archived. Now we are going to show why we can't place 9 or more bishops.
A bishop move like this:
Meaning that it can only attack in this way.
We will not place any bishops at a5 to e5 and a1 to e1. Here is a possibility:
Which is only 5 bishops.
Now, we will place bishops at center, up and down. Note that if we place bishops at center, we cannot place it at corner. Here is a possibility:
Which is only 7 bishops.
Now, we will place bishops at corner, up and down. Here is a possibility:
Which is only 6 bishops. Now, we have only one strong choice. Which is to place the bishops at only at upside and downside.