Don't Guess 2 High Or 2 Low 2 Often!
You are asked to guess an integer between 1 and N inclusive.
Each time you make a guess, you are told either
(a)
you are too high,
(b)
you are too low, or
(c)
you got it!
You are allowed to guess too high twice and too low twice, but if you have a 3 rd guess that is too high or a 3 rd guess that is too low, you are out.
What is the maximum N for which you are guaranteed to accomplish this?
Clarification
: For example, if you were allowed to guess too high once and too low once, you could guarantee to guess the right answer if
N
=
5
, but not for
N
>
5
. So, in this case, the answer would be
5
.
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Nice! Great question, I got to 18 before giving up :(
Log in to reply
Whoa... so close... Glad you liked it! Does the 19 solution make sense?
Log in to reply
Maybe you should put an actual way of arriving at 19 by using that. I tried but concluded that is impossible anyways so that might help to understand it better anyways.
Log in to reply
@A A – Basically, the strategy for 19 is:
Guess 1: 10
Guess 2: 16 or 4
Guess 3: 19, 13, 7, or 1
Guess 4: 18, 15, 11, 9, 5, 2
Then you know it, and you've only used 2 "too high's" and 2 "too lows" :^)
Log in to reply
@Geoff Pilling – Oh , I see now that the optimal procedure by which the numbers are found isn't actually a symmetrical one as I thought initially which would have given a lower bound. That is , at any step you don't actually have to divide the groups of possible numbers into equal parts and this as a result of the way they behave in a not regular way for different outputs of H and L at some step and therefore characterizes considering this the logical structure of the way the pair of values (H , L) determines the possible outputs thing which indeed I have omitted even if this logical structure may remain implicit in deriving the maximal value for which it works by a formula and therefore taking time understanding the procedure which by itself asks for a direct understanding and therefore for an explicit understanding of logical structure since that explicit understanding is just kept implicit in the formula. Anyways , this is a very beautiful problem and of course solution. In particular for understanding the not completely linear determination of logical structure which can be grasped intuitively though seems to be a little strange if you prefer considering this by a constructive approach or by an understanding of the procedure which describes it and thanks anyways for this beautiful problem and your reply and great solution.
@A A – OK, good idea... lemme think about how to best word it...
Yes, I was doing trial and error unfortunately...
I saw your other question a lot like this one... I had no idea it was 1364... Impressive!
Log in to reply
@Finn C – Yeah... No one got it, so I published this one! :)
Log in to reply
@Geoff Pilling – Love these types of question, especially now that I know a more systematic approach!
There's a right way to do it. You want to make sure that if the first guess is too high, you can do with the number of "too high's" and "too low's" you have left; same for if it's too low. The only difference is that if too high, you have one less "too high" and your next guess has to be lower, and vice versa.
If it helps, you don't have to keep track of everything; only realize that after the first guess, the problem breaks down into two symmetric problems.
You probably didn't realize that the answer must be odd, since to be optimum, the first guess must go in the middle! I figured out the solution for N=15, and since it's incorrect, I just attempted 17 and 19 lol.
@Ivan Koswara Woo hoo... you got it! For a second there I was starting to doubt the answer... Nicely done! If you are interested, here is a harder one.... :)
I built the induction slightly differently. Let N(H,L) be the number of numbers you can distinguish while getting at most H "too high" responses and L "too low" responses. Those numbers may not include 1. They might cover the range from 11 to 19, for instance. Because the only information we get is too high, too low or just right, we won't ever be able to eliminate a number between two numbers that are still possible. That means that the possible numbers will always be a continuous range.
N(H,L) = 1 + N(H-1,L) + N(H,L-1) N(0,0) = 1 N(-1,anything) = N(anything, -1) = 0 because we've already lost.
From there, N(2,2) = 19, so we can distinguish each of the possible numbers from 1 to 19.
very nice solution. but i have done it manually though.:p
The answer in a general form would be k = 1 ∑ n ( k n ) 2 . Here, n = 3 . Does anyone see any direct relationship (combinatorially)?
Interesting... How did you come up with that?
So is it only when both kinds of choices are equal?
Umm... I just thought since I'd seen the one with 10 too highs then I thought this would be small, so I guessed 17 then 15 and finally 19 which was the answer and I'm like OMG OMG OMG I got it right! Not instructive, but still funny.
yeah, ! you were lucky ! :)
True, Shubham Dhull!
I have used Permutation and Combination for the approach.
We are allowed to make (a maximum of) 4 Guesses after which (or within which) we have to arrive at an answer.
To start with, we have to guess an integer (Say X) . After each Guess, we have to make a calculated decision to make the next guess so that we are not out.
So the outcomes of the 4 Guesses could be in the following order ( H "too high" and L "too low")
| L L H H |
| L H L H |
| L H H L |
| H L L H |
| H L H L |
| H H L L |
Since maximum 2 H and maximum 2 L are allowed.
Total number of different Decision paths for guesses from among 1 t o N is hence
( C o m m o n O u t c o m e H C o u n t ) ! ( C o m m o n O u t c o m e L C o u n t ) ! ( T o t a l D e c i s i o n s ) !
OR
2 ! x 2 ! 4 ! = 6
Which is also apparent from the Table Above.
In each Path e.g. H L H L , H H L L , . . . . there can be total 4 numbers considering each H or L
But the Paths are joined like a tree with Branching from common nodes of H or L as shown below
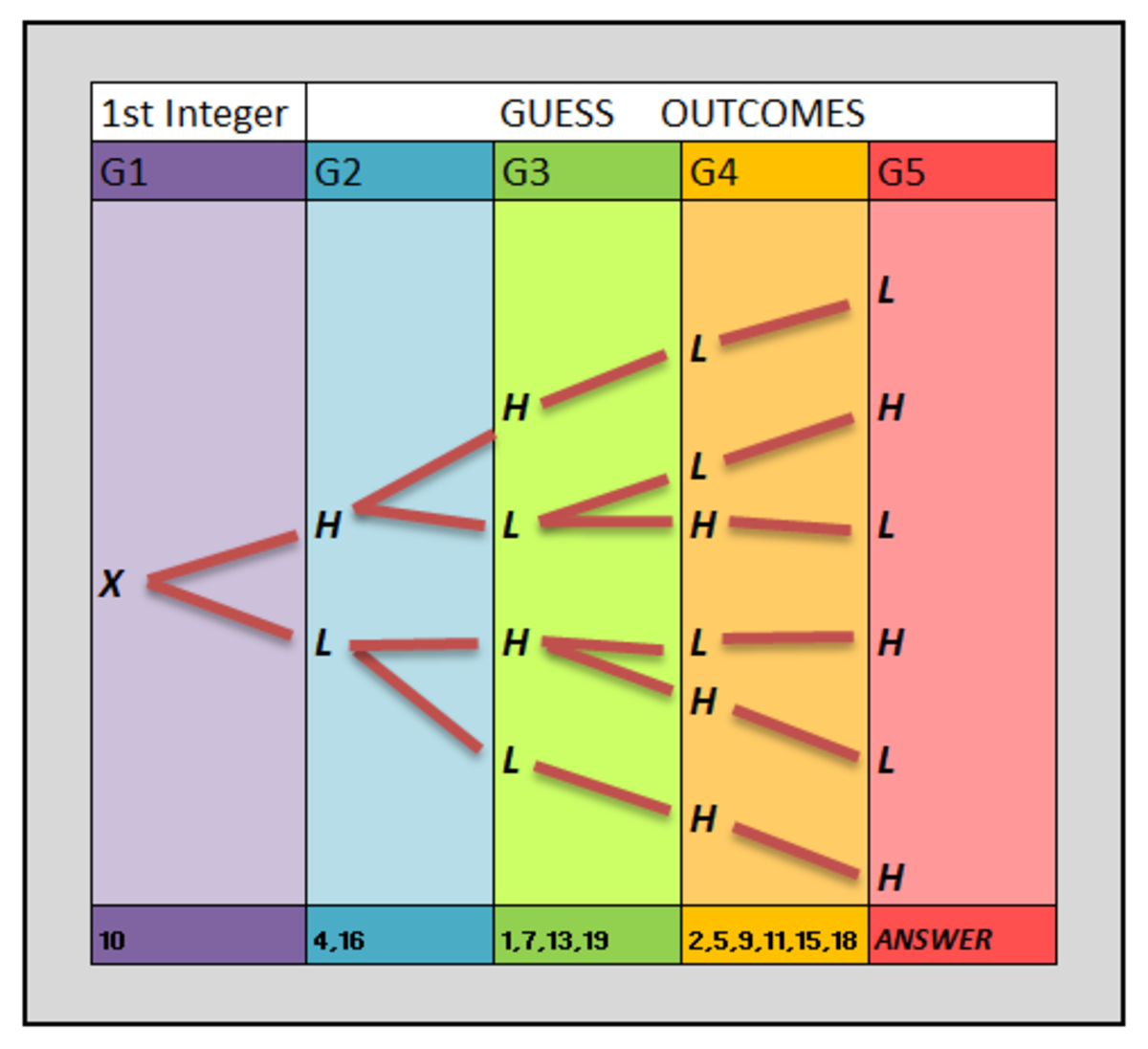
So, if X is one among i items from among 1 t o N Then i − 1 = 1 8 from the tree above.
Hence i = 1 9
Relevant wiki: Information Compression
Every time you take a guess, you divide the problem up into two new problems... One where you reduce your number of "too low" guesses by 1 , and one where you reduce your number of "too high" guesses by 1 . And, the new number N is either all the ones above your guess or all the ones below your guess. So, the recursive equation can be defined as follows:
Let N ( H , L ) = The maximum number you can accomplish this in given that you can get only get H "too high"s and L "too low"s, then...
N ( 0 , L ) = L + 1
N ( H , 0 ) = H + 1
N ( H , L ) = 1 + N ( H − 1 , L ) + N ( H , L − 1 )
Using this, N ( 2 , 2 ) = 1 9
Basically, the strategy for 19 is:
Guess 1: 10
Guess 2: 16 or 4
Guess 3: 19, 13, 7, or 1
Guess 4: 18, 15, 11, 9, 5, 2
Then you know it, and you've only used 2 "too high's" and 2 "too lows" :^)