Don't loose hope-2
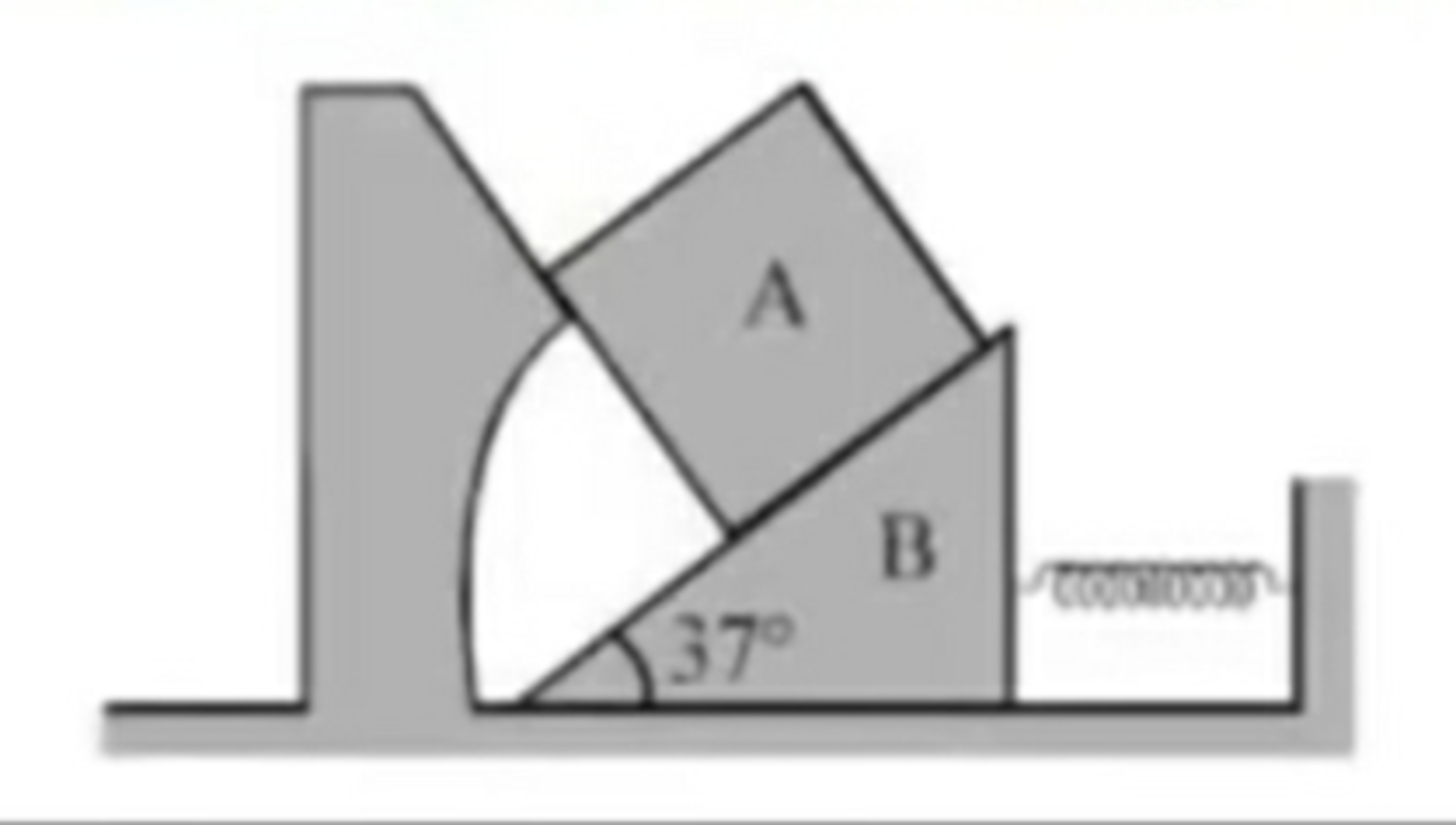
In the figure shown, all surfaces are smooth and block A and wedge B have mass 10 kg and 20 kg respectively. Find the sum of normal reaction between block A and B, spring force and normal reaction of ground on block B.If the whole system is in equilibrium.
Take g= 1 0 m / s 2
Sin(37)=3/5
It is not an original problem .
The answer is 392.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase very nice solution.
@Steven Chase ,i have updated the question,thanks!
Btw nice solution.
Thanks for updating the problem statement by specifying that the system is in equilibrium.
Log in to reply
It would be good to specify in the problem statement to take sin ( 3 7 ∘ ) = 0 . 6 as doing so will give the exact integer answer. In reality, sin ( 3 7 ∘ ) = 0 . 6
Log in to reply
@Karan Chatrath
You were talking that, and now??
Isn't it a contradiction?
Log in to reply
@Talulah Riley – I'm sorry, I don't understand what you are saying
Because you have given an integer answer, you have to give the values of sin 3 7 ° and cos 3 7 ° as 5 3 and 5 4 respectively.
(1) Normal reaction force between the block and the wedge is 1 0 g cos 3 7 ° = 8 0 N
(2) Spring force is 1 0 g sin 3 7 ° cos 3 7 ° = 4 8 N
(3) Normal reaction of ground on the wedge is 2 0 g + 1 0 g cos 2 3 7 ° = 2 6 4 N
Therefore their sum is 8 0 + 4 8 + 2 6 4 = 3 9 2 N.
There are a few problems here, given that the requested answer is in integer format. First, it needs to be stated that the gravitational acceleration is 1 0 . And then, the answer is not actually an integer, so it needs to be stated to round to the nearest whole number.
Aside from that, we are solving a system of four equations for four unknowns. The first two equations are for mass A and the last two are for mass B.
F 1 ≈ 6 0 . 1 8 F 2 ≈ 7 9 . 8 6 F 3 ≈ 4 8 . 0 6 F 4 ≈ 2 6 3 . 7 8 F 2 + F 3 + F 4 ≈ 3 9 1 . 7 0