Don't try to multiply!
( 1 + cos 9 π ) ( 1 + cos 9 3 π ) ( 1 + cos 9 5 π ) ( 1 + cos 9 7 π )
The value of the expression above can be expressed as Q P , where P and Q are coprime positive integers , find Q − P .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
The given cosines are the roots of the polynomial f ( x ) = 3 2 3 2 x 4 − 1 6 x 3 − 2 4 x 2 + 8 x + 2 . So what is asked is f ( − 1 ) which is equal to 1 6 9 . This method justifies the name of the problem.
Did almost the same. But why is the problem called "don't multiply"? We're using multiplication at some stage, you know!
Log in to reply
Multiplication solves this essentially easier because one has only to transform 0.5625 into a proper fraction!
Log in to reply
But how do you find the value of all the cosines without calculator?
Log in to reply
@Anupam Nayak – Look here: http://mathworld.wolfram.com/TrigonometryAnglesPi9.html
Then use addition theorem.
( 1 + cos 9 π ) ( 1 + cos 9 3 π ) ( 1 + cos 9 5 π ) ( 1 + cos 9 7 π )
Using cos ( π − x ) = − cos x we get:
( 1 − cos 9 8 π ) ( 1 − cos 9 6 π ) ( 1 − cos 9 4 π ) ( 1 − cos 9 2 π )
Using 1 − cos 2 x = 2 sin 2 x we get:
2 4 × sin 2 9 4 π × sin 2 9 3 π × sin 2 9 2 π × sin 2 9 π
Now using sin ( π − x ) = sin x we get:
2 4 sin 9 π sin 9 2 π sin 9 3 π sin 9 4 π sin 9 5 π sin 9 6 π sin 9 7 π sin 9 8 π
Now using the famous identity k = 1 ∏ n − 1 sin n k π = 2 n − 1 n we get:
= 2 4 × 2 8 9 = 1 6 9
I like your solution. Do you know of a proof of the last identity you use?
We can use half angle identity and then use the popular identity cosxcos(60-x)cos(60+x) = cos3x / 4
Yes , thats my one of the favourite trigonometric identities
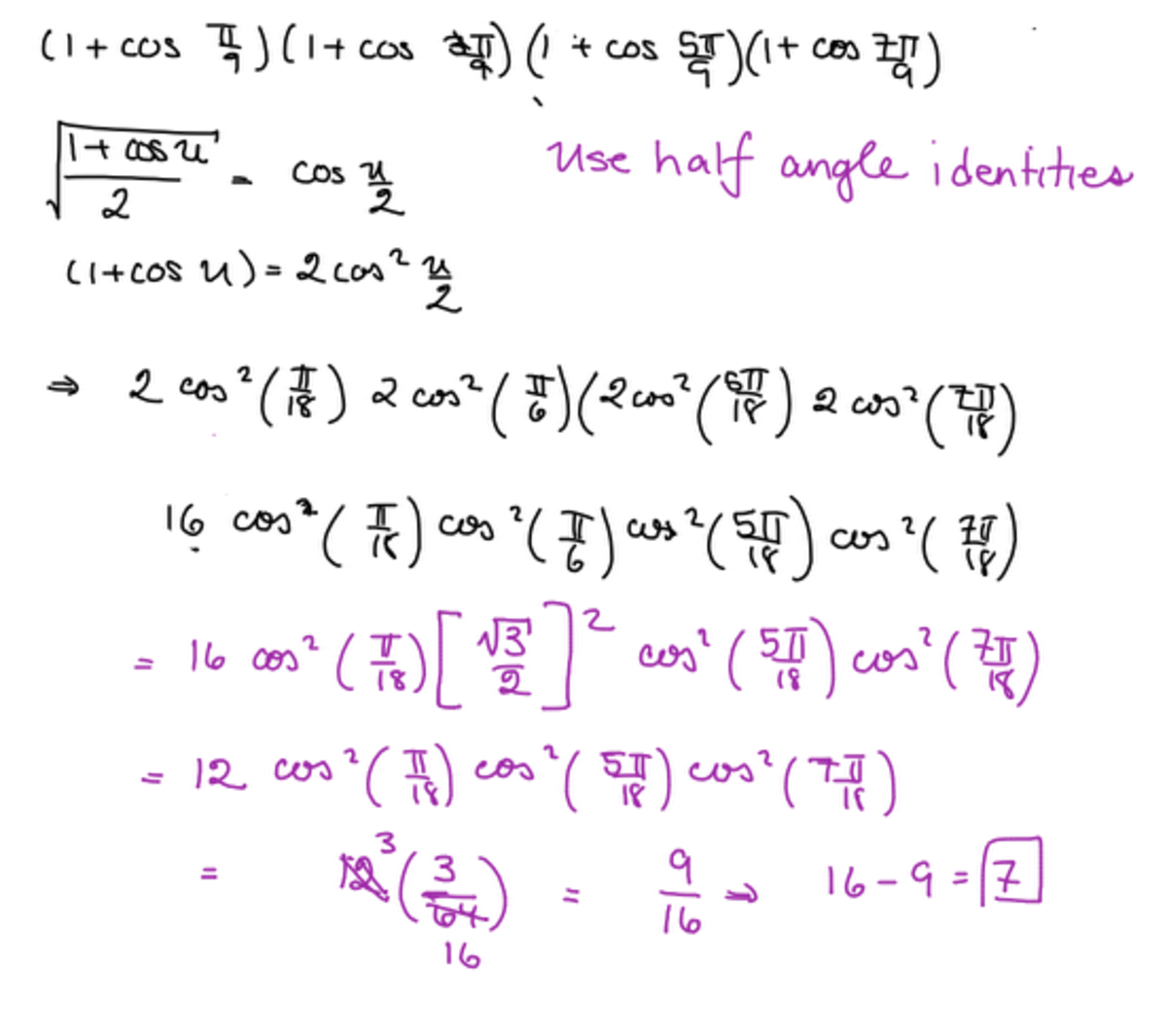
R = ( 1 + cos 9 π ) 1 + ( 2 1 ) = 2 3 ( 1 + cos 9 3 π ) ( 1 + cos 9 5 π ) ( 1 + cos 9 7 π ) Use 1 + cos 2 x = 2 cos 2 x .
R = 3 ( 2 cos ( 1 8 π ) cos ( 1 8 5 π ) cos ( 1 8 7 π ) ) 2
Use 2 cos A cos B = cos ( A + B ) + cos ( A − B )
R = 3 ⎝ ⎜ ⎜ ⎛ ⎝ ⎜ ⎜ ⎛ 2 1 cos ( 3 π ) + cos ( 9 2 π ) ⎠ ⎟ ⎟ ⎞ cos ( 1 8 7 π ) ⎠ ⎟ ⎟ ⎞ 2
= 4 3 ( cos ( 1 8 7 π ) + 2 cos ( 1 8 7 π ) ( 9 2 π ) ) 2
= 4 3 ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ cos ( 1 8 7 π ) + − cos ( 1 8 7 π ) cos ( 1 8 1 1 π ) + cos ( 6 π ) ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ 2
= 1 6 9
∴ 1 6 − 9 = 7