Don't try x = y = z
Let x , y , z be real numbers such that x 2 + y 2 + z 2 = 1 . Let the maximum possible value of 6 x y + 4 y z be A .Find A 2 .
This problem is inspired by Joel Tan .
The answer is 5.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Your solution is awesome! BTW what motivated you to let a + b = 1 ?
Log in to reply
When i saw xy & yz AM-GM inequality came to my mind , y was common(in xy and yz) so i thought i should break it in such a way so that x^2+y^2+z^2=1 can be used
How do you come up with such elegant solutions??AWESOME SOLUTION!!
Can you clarify a doubt please? Can we use AM GM inequalities separably for different expressions and then combine them to give a solution when the variables are connected by a relation?
Log in to reply
yes if a>b & c>d then (a+c)>(b+d)
a,b,c,d can be dependent or independent of each other
Or do we have to use it on the whole expression
Or
( x 2 + 2 2 6 y 2 ) + ( 2 2 1 6 y 2 + z 2 ) ≥ 2 2 2 ( 6 x y + 4 y z )
Log in to reply
how can you apply am gm here
Log in to reply
First applying AM-GM on
( x 2 + 2 2 6 y 2 ) ≥ 2 2 2 6 x y
then on ( z 2 + 2 2 1 6 y 2 ) ≥ 2 2 2 1 6 z y
Adding both we get the desired expression.
Log in to reply
@Department 8 – But AM GM is only for positive reals
Log in to reply
@Dev Sharma – Sorry did not saw that but this solution also uses AM-GM
Log in to reply
@Department 8 – There is no problem in applying AM GM here because you are applying it on squares which is always positive
@Department 8 – what motivated you to have 6 and 16 there?
Same way. nice solution brah!
Log in to reply
Brah? Elaborate
Log in to reply
@Department 8 – a highly modified and technical version of "bro" which means a brother or a brother-like freind. should i explain further?
Log in to reply
@Shreyash Rai – Sometime it's not good to write these which can men double meaning.
Log in to reply
@Department 8 – Never considered if there was an other meaning but allright I get the point.
Let y = cos θ , x = sin θ cos ϕ and z = sin θ s i n ϕ and use the fact that A sin ϕ + B cos ϕ has a maximum value A 2 + B 2 Putting in 6 x y + 4 y z = 2 y ( 3 x + 2 2 z ) and taking common sin θ outside the bracket, and using the above mentioned maximizing A = 2 2 / 2 .
Absolutely Fantastic.
Nice use of trigonometric inequalities!!
Same here!!
Let 6 x y + 4 y z ≤ k [ x 2 + y 2 + z 2 ] for a real number k . This way we just simply need to find the value of k , which obviously is the maximum value of the above expression.
From AM-GM we have k 1 = 6 x y ≤ 2 a 1 x 2 + 2 a 2 y 2 for some real a 1 , a 2 . With the same way we got k 2 = 4 y z ≤ 2 a 3 y 2 + 2 a 1 z 2
Therefore, k 1 + k 2 ≤ 2 a 1 [ x 2 + z 2 ] + [ 2 a 2 + a 3 ] y 2 We know that a 1 a 2 = 6 and a 3 a 1 = 1 6 While we want to find a 1 with a 2 + a 3 = a 1
Therefore, a 1 6 + a 1 1 6 = a 1 We can easily get a 1 = 2 2 . Then we have k 1 + k 2 ≤ 2 2 2 [ x 2 + y 2 + z 2 ] = 2 2 2 = A . Therefore A 2 = 2 1 1 .
Did same way
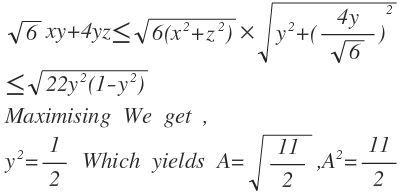
Rajen Sir's solution is probably the best but i solved this by only algebra,
L e t a & b a r e s u c h t h a t a + b = 1 N o w A M ≥ G M ⇒ 2 x 2 + a y 2 ≥ x y a & 2 b y 2 + z 2 ≥ y z b i f b a = 4 6 ⇒ a = 1 1 3 , b = 1 1 8 ⇒ x y a + y z b ≤ 2 x 2 + a y 2 + 2 b y 2 + z 2 ⇒ x y 1 1 3 + y z 1 1 8 ≤ 2 1 ⇒ 6 x y + 4 y z ≤ 2 2 2 ⇒ A = 2 2 2 o r A 2 = 2 1 1 = 5 . 5