Don't you have any original ideas?

Logic Level 5

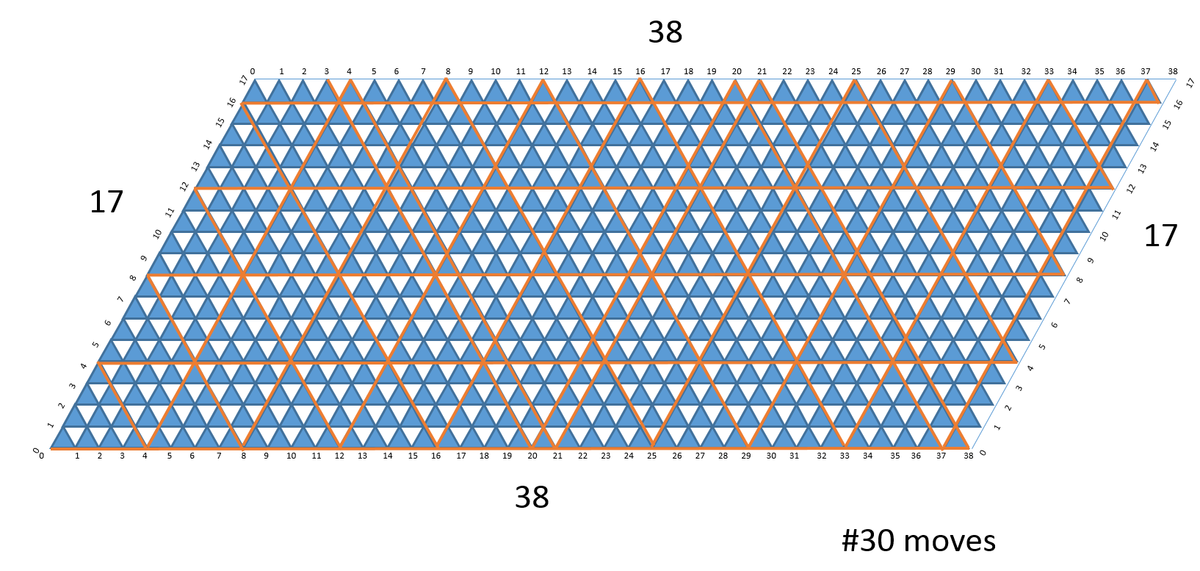
You have two water bottles both empty, one with the capacity to hold 38 liters of water and the other 17 liters and an endless supply of water. What is the minimum number of moves required to get 3 liters?

Details and assumptions :

Filling a bottle, emptying a filled bottle and transferring water from one bottle to another counts as a move.
While filling the bottle, you have to fill it to the bottle's maximum.

Inspiration .

The answer is 30.

3 solutions

Arjen Vreugdenhil
May 22, 2016

Let the capacities of the bottles be $A > B$ . We call an amount in a bottle "trivial" if the bottle is empty or completely filled.

Starting with two empty bottles, we must start by filling one of them. Now consider:

A. After every move, one of the bottles has a trivial amount.

B. After the first move, it is meaningless to fill or empty the bottle with the non-trivial amount.

C. Two successive fillings or emptyings can always be avoided. The same is true for two successive transfers. Thus we must follow a pattern of transfer -- filling/emptying -- transfer -- filling/emptying -- etc. We always transfer from the bottle just filled, or to the bottle just emptied; we always fill or empty the bottle with the trivial amount. All in all, there is only one meaningfull sequence to follow.

D. Only filling and emptying can change the total amount in the bottles. The change is equal to $\pm A$ or $\pm B$ . The overall result is $x \mapsto x + mA + nB$ in $2(|m| + |n|)$ moves.

How many moves are needed to get from zero to three liters? We must solve $0 + 38 m + 17 n = 3$ minimizing $|m|$ and $|n|$ . Note that $4 = 38 - 2\cdot 17$ ; $3 = 5 \cdot 4 - 17 = 5(38 - 2\cdot 17) - 17 = 5\cdot 38 - 11\cdot 17$ .

Thus we can get to 3 liters in $2(|5| + |-11|) = 32$ moves. However, we assumed that the first move was a transfer (which may be omitted) and the last move a filling or emptying (which does not create the 3-L bottle), so we subtract two, leaving $\boxed{30}$ moves.

This is a very systematic approach. Thank you!

Pi Han Goh - 5 years ago

Magne Myhren
Jul 26, 2015

Inspired by https://www.youtube.com/watch?v=0Oef3MHYEC0 , I made a similar chart and counted the number of lines.

ahah nice!!!!

Pi Han Goh - 5 years, 10 months ago

Pi Han Goh
Jun 28, 2015

$\Large{\begin{aligned} 0 & , & 0 \\ 38 & , & 0 \\ 21 & , & 17 \\ 21 & , & 0 \\ 4 & , & 17 \\ 4 & , & 0 \\ 0 & , & 4 \\ 38 & , & 4 \\ 25 & , & 17 \\ 25 & , & 0 \\ 8 & , & 17 \\ 8 & , & 0 \\ 0 & , & 8 \\ 38 & , & 8 \\ 29 & , & 17 \\ 29 & , & 0 \\ 12 & , & 17 \\ 12 & , & 0 \\ 0 & , & 12 \\ 38 & , & 12 \\ 33 & , & 17 \\ 33 & , & 0 \\ 16 & , & 17 \\ 16 & , & 0 \\ 0 & , & 16 \\ 38 & , & 16 \\ 37 & , & 17 \\ 37 & , & 0 \\ 20 & , & 17 \\ 20 & , & 0 \\ 3 & , & 17 \\ \end{aligned}}$

Moderator note:

There is a one-line proof that we indeed have the minimum number of steps required.

Hint: Apply the Euclidean Algorithm . How do those numbers correspond to what we have above?

Nicely done. I did it the same way. Is there a way to generalise it?

A Former Brilliant Member - 5 years, 11 months ago

I don't have the complete justification for the generalization but yes there is.

For this particular example, we want to solve for the integers $x,y$ such that $38x + 17y = A$ where $A < \text{min} (17,38)$ . Then the answer is simply $2|x+y|$ .

Pi Han Goh - 5 years, 11 months ago

How do you get that result? And how do you choose the solution for the integer equation (38x + 17y = A)?

In this case (38x + 17y = 3), you get the desired result with the solution x=-12, y=27, 2|x+y| = 2*15=30.

But x=5, y=-11 is also a valid solution, and it actually describes better the process used to get 3 liters in 30 steps, but using these values you would get 2|x+y| = 2*6=12.

Andrés Castillo - 5 years, 9 months ago

@Andrés Castillo – I guess my justification is wrong then... Do you have a clue on how to deal with this Euclidean Algorithm?

Pi Han Goh - 5 years, 9 months ago

@Pi Han Goh – I think the general solution would be something like this:

If you have two bottles with capacity $a$ and $b$ liters, and you need exactly $n$ liters, (where $n<min(a,b)$ is a multiple of $gcd(a,b)$ ), find the integer solution to the equation $ax + by = n$ that minimizes the value of $|x|+|y|)$ .

In any integer solution of the equation either $x$ or $y$ will be positive, and the other one will be negative. Assuming $x$ as the positive one, the equation can be translated to a unique sequence of operations, starting form $0$ , and in each step adding $a$ or substracting $b$ such that the total result is alway between $0$ and $a+b$ .

If the final step in this sequence is an addition, then you can get a bottle with exactly $n$ liters in $2(|x|+|y|)-1$ steps.

If the final step is a substraction, then you can get it in only $2(|x|+|y|)-2$ steps.