Double Diagonal Power Tower
Let A = 2 2 2 ⋅ ⋅ ⋅ and B = ⋱ 2 2 2
Then it is true that:
Note: B is no t a nested tetration.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
How do you prove that B is defined? (The limit might not exist, which means they are not comparable and thus there's no answer among the options.)
Likewise with A , although you sidestepped the entire thing with "computed via classical means".
Log in to reply
2 2 = 2 2 1
Well for A I sidestepped it because it is a classic problem (the 2 versus 4 dilemma).
For B , well, I was too lazy to check that it was defined. But it had only one solution and it looked about right, so I assumed. I'm sure it can be proven to exist in some way or another. Please tell me if this is false though.
Log in to reply
I think you should prove one of the four requirements here .
Log in to reply
@Pi Han Goh – I'm pretty sure by 2 2 he meant 2 2 1 ; the 2 at the left is the index of the root.
Log in to reply
@Ivan Koswara – I interpreted as a nested tetration function.
Log in to reply
@Pi Han Goh – This is what fooled me aswell! Overthought the problem.
Could someone tell me how one can go about computing the value of A by classical means?
A can also be equal to 4
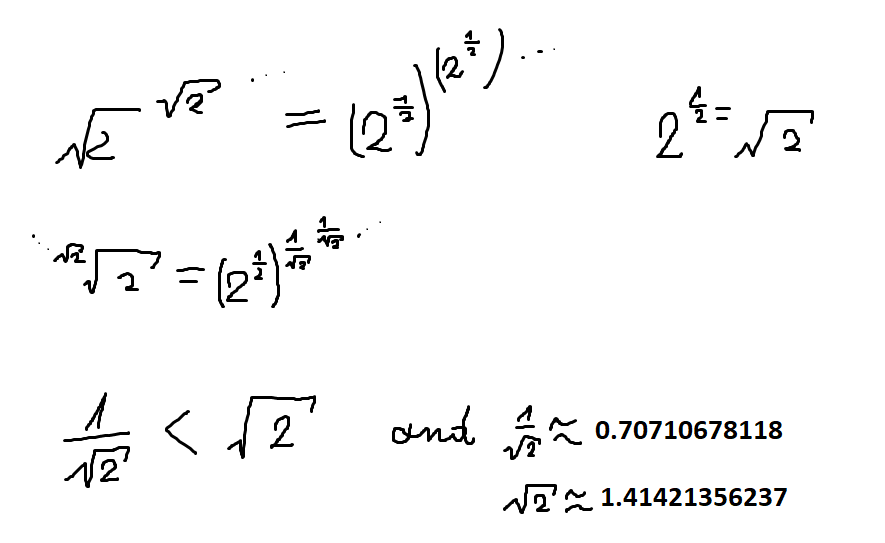 as it "goes by" A is going to get higher values of the exponent and it'll get bigger while B is going to get smaller fractions as an exponent (so it'll be 'rooting' harder over time)
So basically A = sqrt2 ^ x when x > 1 and B = sqrt ^ x' when x' < 1 which means A > B
as it "goes by" A is going to get higher values of the exponent and it'll get bigger while B is going to get smaller fractions as an exponent (so it'll be 'rooting' harder over time)
So basically A = sqrt2 ^ x when x > 1 and B = sqrt ^ x' when x' < 1 which means A > B
First, the value of A can be computed via classical means to arrive at A = 2 .
We see that B satisfies B = B 2 .
Note that if B = 2 , then 2 > 2 ⟹ L H S > R H S .
Also, note that f ( B ) = B is continually increasing while f ( B ) = B 2 is continually decreasing for B > 0 ; thus, along with the fact that when B = 2 ⟹ L H S > R H S , the (unique) root of B = B 2 satisfies B < 2 .
Thus, A > B