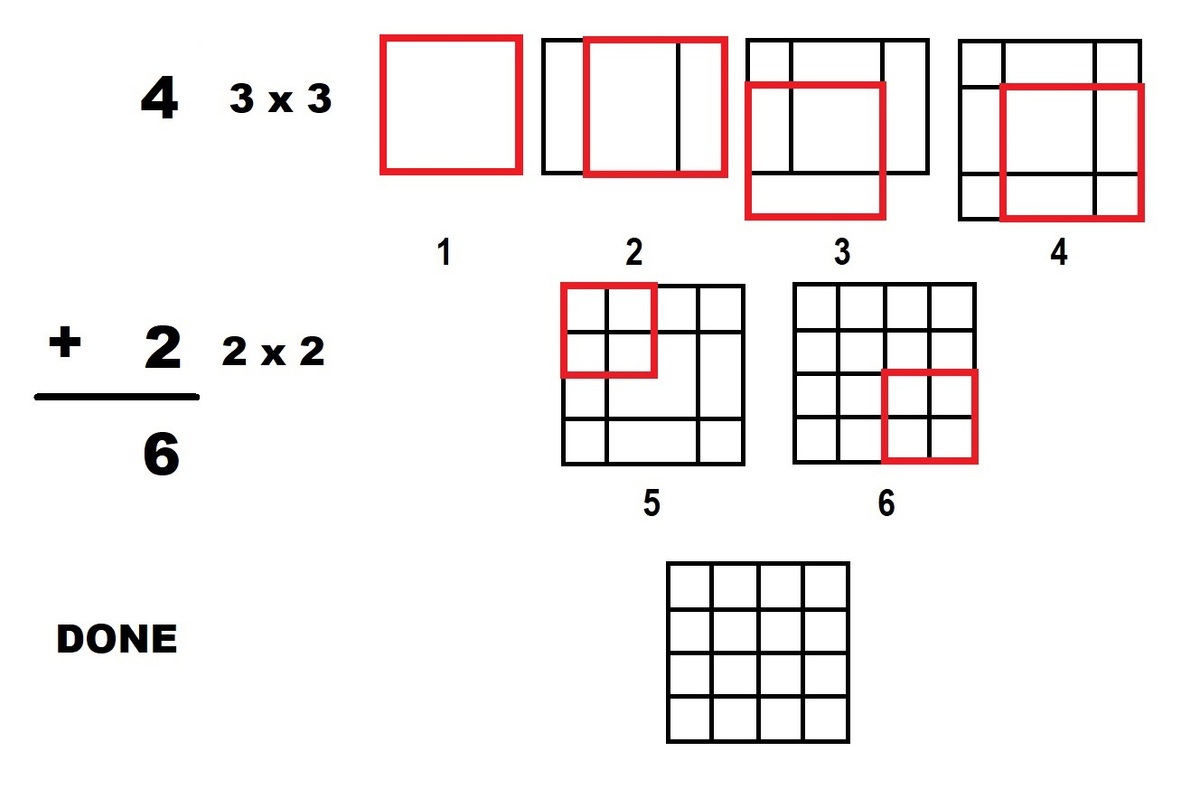
Drawing Squares
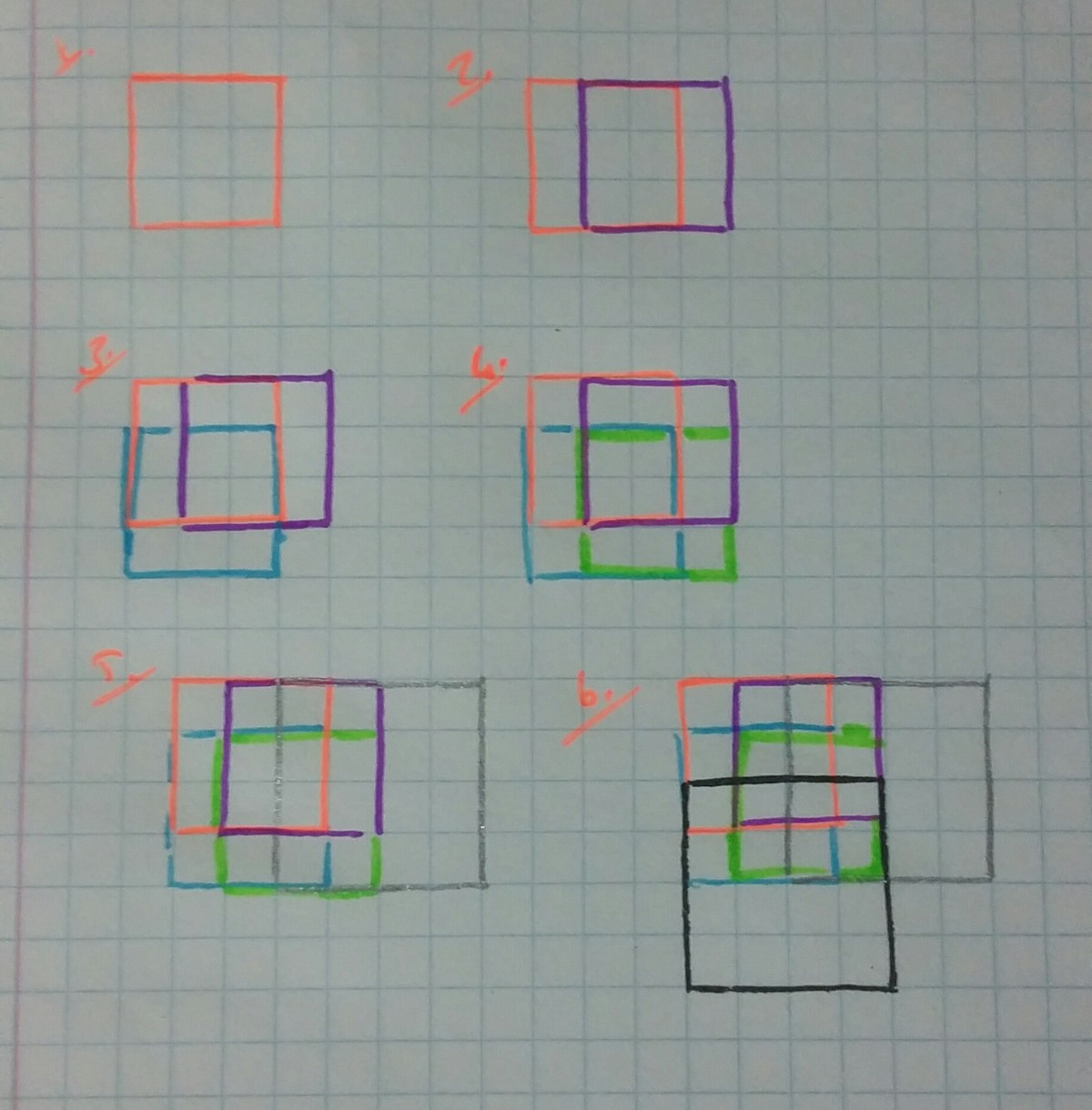
As illustrated below, Alice needs to draw just 3 (red) squares to create 4 unit squares.
What is the least number of squares she needs to draw to create 16 unit squares?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Moderator note:
Proof that 6 is minimal (when forming the 16 unit squares in a 4 by 4 manner):
12 edges are marked. It is impossible to draw a square that includes more than 2 of the marked edges at the same time. Therefore 6 squares are needed.
We can draw sixteen small squares with the dotted line first, and then fill in the dotted line as much as we can when we draw squares, so that we can find the least number of squares after we try one or two times.
Log in to reply
Maybe you can submit this as a solution? More people will notice and appreciate this idea, that way.
Log in to reply
Unluckily, I do all the work, draw squares on the note book and take pictures of them. But just when I was ready to submit it, I found I accidentally chose the wrong answer. As a result of this, I am not given the right to submit solution. QAQ...
how about x=y^0.5, where y is the number of edges on the "big square" (40 for the case of 16 unit squares), and x is the number of needed drawn red squares (rounded down) (any proof for this?)
still cant see general formula like the x=y^0.5 conjecture, which topic has some info about this?
Log in to reply
In general, it is hard to have such nice answers for combinatorial problems. Did you check if this conjecture holds for some small y's?
Log in to reply
works for 2,3 and 4x4 grid, but not for 5, or even 1; seems the minimal for 5x5 grid is 9 drawn squares, trying to find another solution, or minimal, ty ken and agnishom
Log in to reply
@Eliud Alejandro Maldonado Sanchez – 5x5 can be done with 8 squares.
In a 5x5 grid, there are y = 60 edges, so by your formula x = 7. But the minimal x is 8 (see challenge master's note and my comment).
You shouldn´t use only 2x2 and 1x1 squares ?
This type of problem seems kinda couterproductive, because if the purpose is to take a square to 16 equal units with the least moves; well drawnig 6 squares is equal of drawing 6x4=24 lines. Instead draw one square first that would be 4 lines. Then add to it 2 sets of 3 lines perpendicular to each set of parallel sides of the primary square which woul be 6 lines. And there you have it. 16 equal sized squares inside one at the cost of drawing only 4+6=10 lines, and on top of it, all the lines are the same size.
Honestly I don't really understand this problem that much. I just thought that the bigger the number of squares is the less you will have to draw after. How does this problem work? I would rate this problem a 7 because I didn't really get how to do it. I didn't really get it so I just tried to follow the instructions as much as possible even though I was kind of confused.
This is what I worked out.
What does "Of the choices given" mean?
Does this solution use means beyond "the choices given" and is thus not valid?
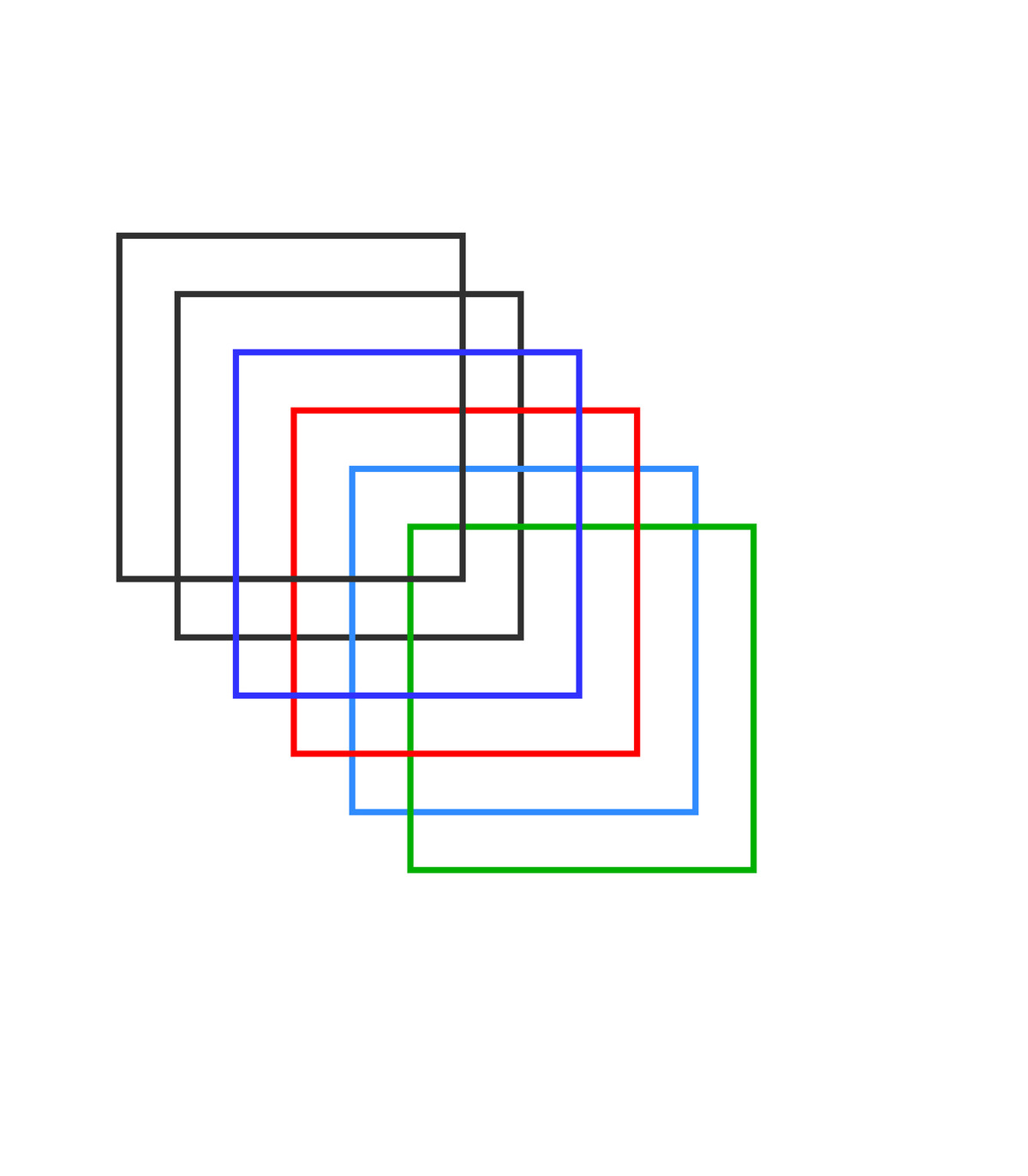
I think “Of the choices given” just refers to the multiple choice nature of the question. Given the limited instructions, this seems a perfectly valid solution. You are thinking outside the square !
Log in to reply
It is a poorly worded puzzle. The example pictures seem only to require that the grid be built from squares.
A solution above has the interesting feature of using pairs of successively smaller squares 3x3, 2x3, 1x1 that arguably follows a pattern from the example that my solution does not,
how is this a basic question. i've done advanced problems easier than a proof like this.
Log in to reply
Actually there is no proof here. Maybe there is a shorter way. Who knows from this? This only illustrates how I arrived at the accepted answer. There is no demonstration here that a genuine minimum has been achieved. As shown here, it is no better than a good guess.
GOOD. put how can I think of it ?
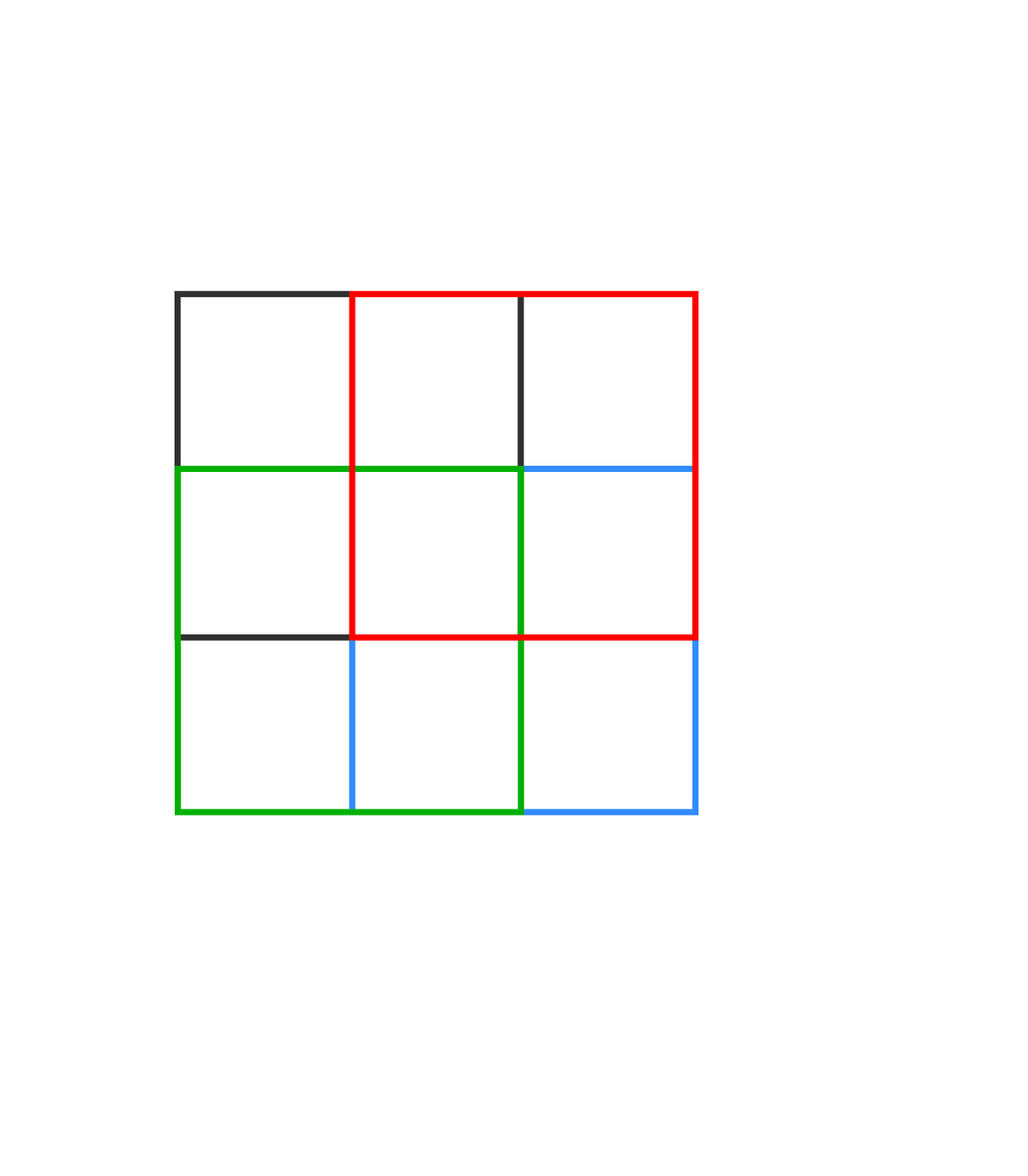
I thought that would have broken the rules. My understanding was that you couldn't draw lines that weren't completely part of the final squares (unlike 5 and 6). Is it still possible with these constraints? (the best I could do was 7: I started with the 4×4 square, then a 1×1, a 2×2 and a 3×3 on each of two opposite corners.)
Log in to reply
Replace the step 5 and 6 with 2x2 square in top left and bottom right (or top right and bottom left) will only use 6 square and would not draw any lines out of the 4x4 parts.
Just make the last two a 2x2 squares and put them diagonly to each other and the puzzle is done
Still wondering what "Of the choices given" means.
Don't need to draw anything.
16 squares within 1 square, shared edges = √16 = 4
non shared edges = √shared edges = √4 = 2
shared + non shared = 4 + 2 = 6
Number of squares(rule whole squares) (ie not all counted or else one can get 16 squares in a much lesser number. //// Squares created (if it wasnt whole squares two would be 3)
| 1 = 1 |
| 2 = 2 |
| 3 = 4 |
| 4* = 9 |
| 5 = 13 (6*2+1) |
| 6 =21 - r(7*2+1) |
| 7 = 31 -r(8*2+1) |
| Sn=n-2(a1 + a(n-2)) + 1 |
| S5 =5-2(1+(5-2))+1 |
| S5 = 3(4) +1 |
| S5 = 13 check |
| S6 = 21 check |
Estimate formula for most (whole)squares created, the estimate should be the number is greater or equal to the first larger number. 8* = 43 = its more since multiple of fours can create different equal shapes. Which makes sense because it gives one an extra corner that completes half as many more of its N number but I haven't checked that. 9 = 57
| answer should be 6 if; |
8* = 43 = its more since multiple of fours can create different equal shapes. Which makes sense because it gives one an extra corner that completes half as many more of its N number but I haven't checked that.
It seems like you have been able to show a general closed form for this. Can you explain how you arrived at it, and how you prove it?
Can it not be solved with only four more squares? Correct me if I'm wrong.
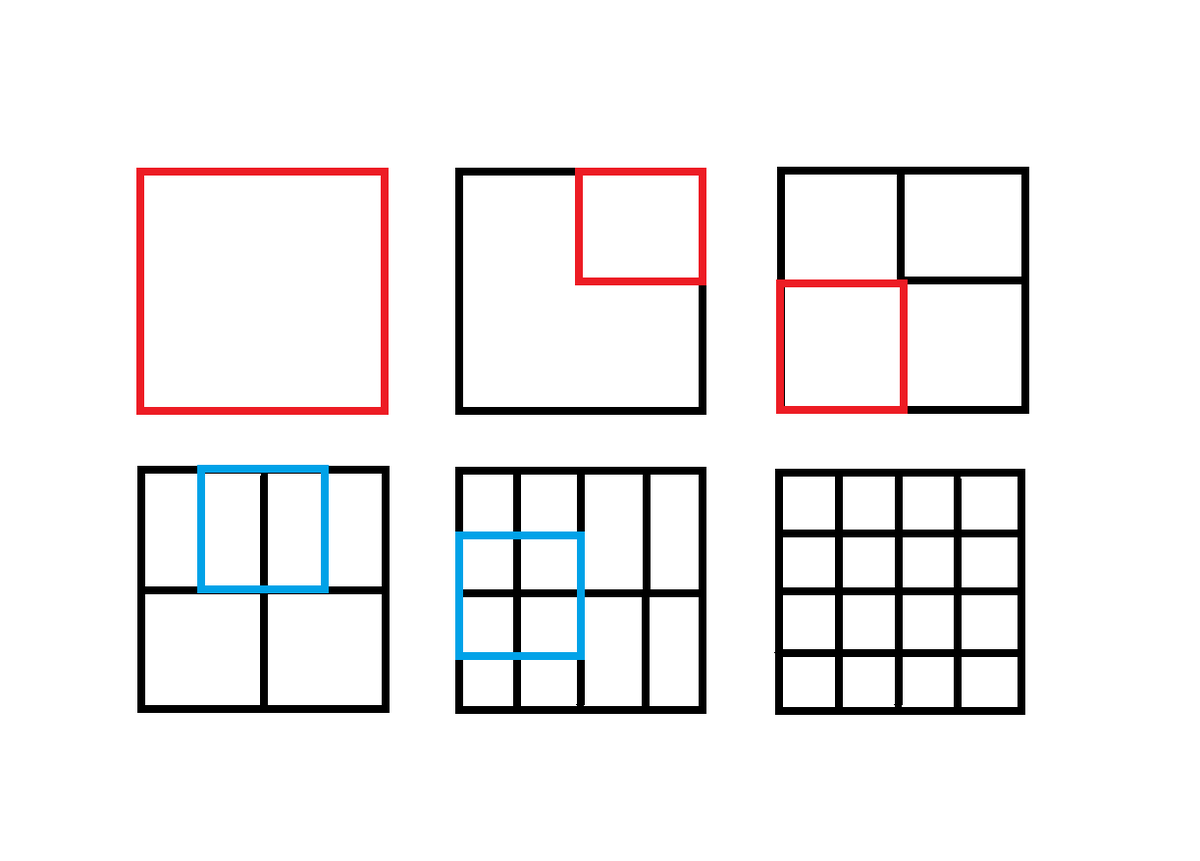
A square on the top middle, bottom middle, middle left, and middle right.
I see how it can be solved with 6, I just wanted to confirm that this way is also correct. I was looking for the least amount of squares to solve it.
See the Challenge Master note at the top to understand why when forming the 16 unit squares in a 4 by 4 manner, we need at least 6 squares. Then, check it against your example, to see if the note is correct or incorrect.
Yeah i Saw 5, by drawing a square in the middle splitting the square into a middle with 4 squares and 4 cornerpieces, and then draw 4 squares in the corners. So even if 4 was somehow not right 5 could as well. Not much out of the box thinking went into this.
Log in to reply
Can you be more explicit / attach an image?
I think you have "draw a square in the middle" and "split the square" and "then draw 4 squares", which gives us 6 squares. However, I am not fully certain about what you are describing.
After the third fig., Can we make one square at one corner and another diagonal corner square in next step .so we get in total 5 steps
(Not a rigorous solution yet)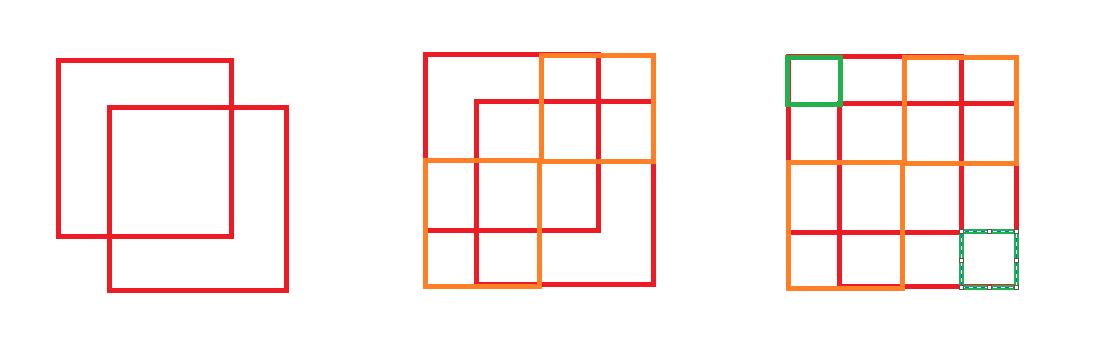
Reds are 3x3, Orange ones are 2x2, Green ones are 1x1.